
一90°。因此可以看出,G(jo)的轨迹与虚轴交点处的频率,就是无阻尼自然频率のn。在极坐标图上,距原点最远的频率点,相应于谐振频率0,。这时G(j)的峰值,可以用谐振频率の,处的向量幅值与=0处向量幅值之比来确定。对于过阻尼情况,当の 增加到远大于1时,G(jの)的轨迹趣近于半圆。这是因为对于强阻尼系统,特征方程的根为实根,并且其中一个根远小于另一个根。因为对于足够大的S值,比较大的一个根对系统影响很小,因此系统的特征与一阶系统相似。133
133 − 90 。因此可以看出, G( j) 的轨迹与虚轴交点处的频率,就是无 阻尼自然频率 n 。在极坐标图上,距原点最远的频率点,相应于谐振频率 r 。这时 G( j) 的峰值,可以用谐振频率 r 处的向量幅值,与 = 0 处向量幅值之比来确定。 对于过阻尼情况,当 增加到远大于 1 时, G( j) 的轨迹趣近于半圆。 这是因为对于强阻尼系统,特征方程的根为实根,并且其中一个根远小于 另一个根。因为对于足够大的 值,比较大的一个根对系统影响很小,因 此系统的特征与一阶系统相似
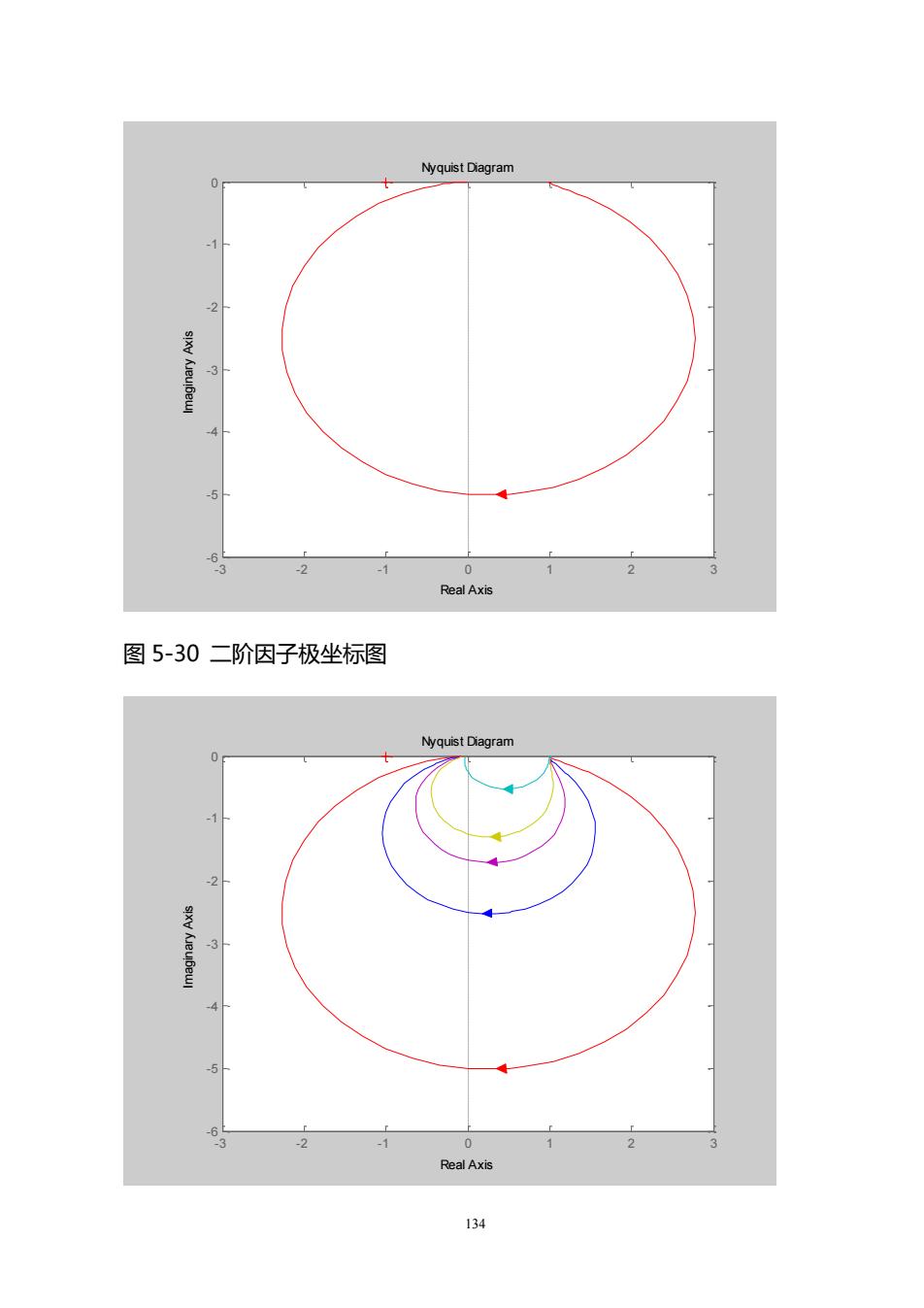
NyquistDiagram-2sxy Keue3-4-56RealAxis图5-30二阶因子极坐标图NyquistDiagram-1-2ere3-560RealAxis134
134 Nyquist Diagram Real Axis Imaginary Axis - 3 - 2 - 1 0 1 2 3 - 6 - 5 - 4 - 3 - 2 - 1 0 图 5-30 二阶因子极坐标图 Nyquist Diagram Real Axis Imaginary Axis - 3 - 2 - 1 0 1 2 3 - 6 - 5 - 4 - 3 - 2 - 1 0
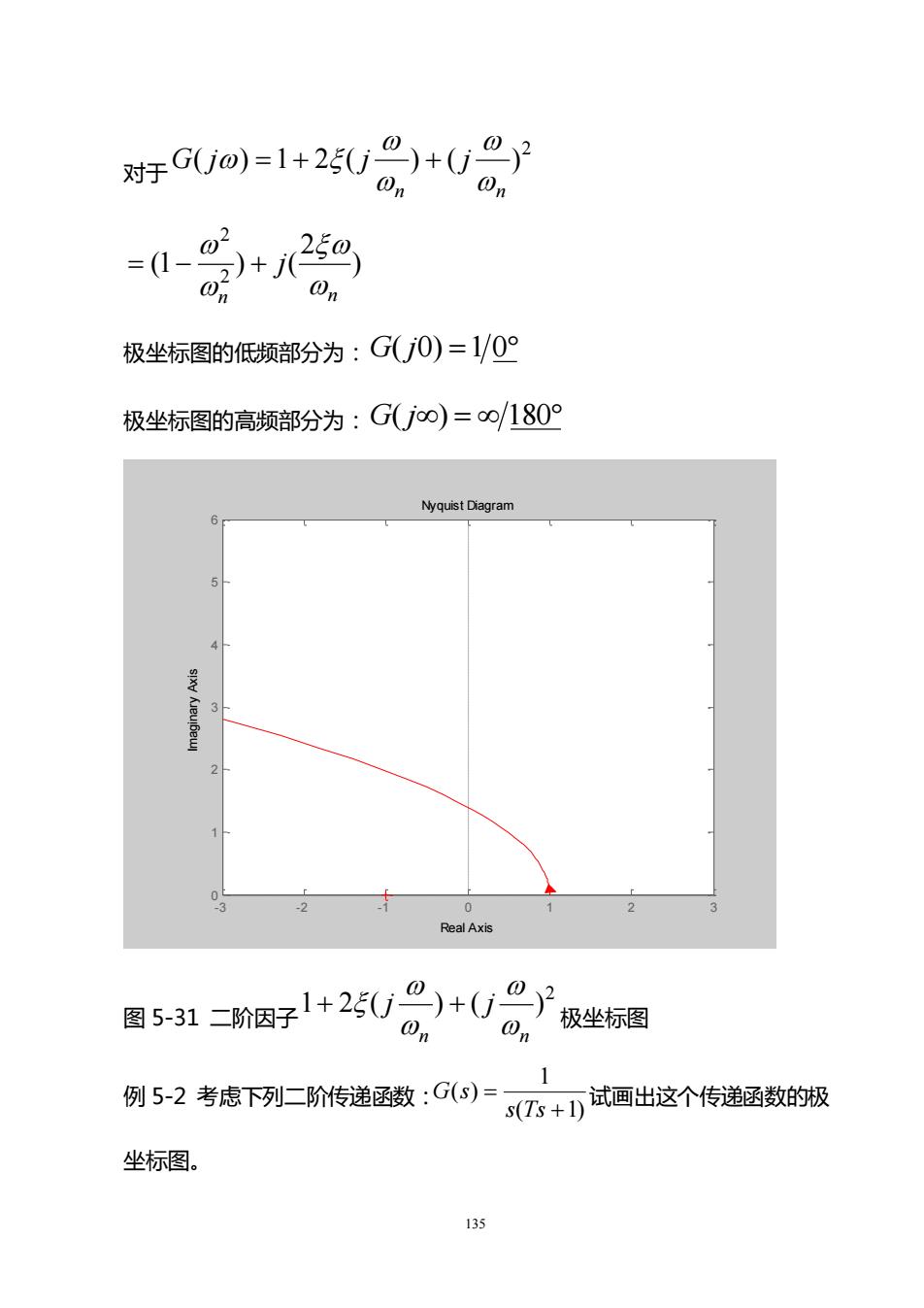
)+(j-对于 G(jo)=1 + 25(j-0C00On极坐标图的低频部分为:G(j0)=1/0°极坐标图的高频部分为:G(joo)=80/180°NyquistDiagramSEXeReal Axis1+ 2E(j图5-31二阶因子极坐标图0例5-2考虑下列二阶传递函数:G(s)=s(Ts+1)试画出这个传递函数的极坐标图。135
135 对于 2 ( ) 1 2 ( ) ( ) n n G j j j = + + ) 2 (1 ) ( 2 2 n n j = − + 极坐标图的低频部分为: G( j0) =1 0 极坐标图的高频部分为: G( j) = 180 Nyquist Diagram Real Axis Imaginary Axis - 3 - 2 - 1 0 1 2 3 0 1 2 3 4 5 6 图 5-31 二阶因子 2 1 2 ( ) ( ) n n j j + + 极坐标图 例 5-2 考虑下列二阶传递函数: ( 1) 1 ( ) + = s Ts G s 试画出这个传递函数的极 坐标图
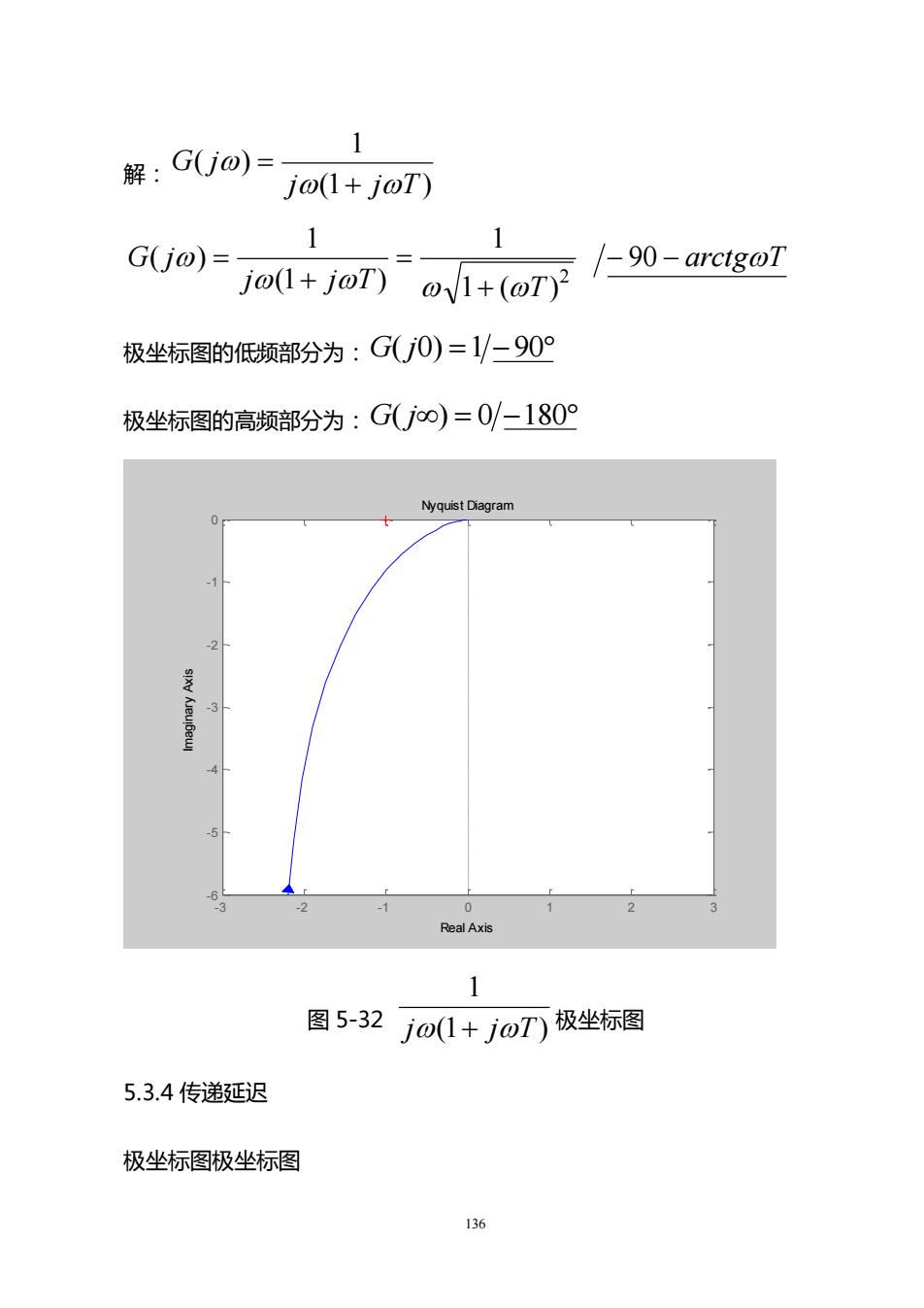
1解: G(j):jo(1 + joT)1G(jo) =- 90-arctgoTjo(l+ joT)0/1+(oT)极坐标图的低频部分为:G(j0)=1/-90°极坐标图的高频部分为:G(joo)=0/-180°NyquistDiagram-2seueReal Axis1图5-32 jo(1+ joT)极坐标图5.3.4传递延迟极坐标图极坐标图136
136 解: (1 ) 1 ( ) j j T G j + = arctg T j j T T G j − − + = + = 90 1 ( ) 1 (1 ) 1 ( ) 2 极坐标图的低频部分为: G( j0) =1 −90 极坐标图的高频部分为: G( j) = 0 −180 Nyquist Diagram Real Axis Imaginary Axis - 3 - 2 - 1 0 1 2 3 - 6 - 5 - 4 - 3 - 2 - 1 0 图 5-32 (1 ) 1 j + jT 极坐标图 5.3.4 传递延迟 极坐标图极坐标图