
第五章回归分析方法 进行回归分析首先是回归函数形式的选择 当只有一个自变量时,通常可采用画散点图 的方法进行选择。 0.1 42 例1合金的强度y(×10Pa)与合金中碳的 0.11 cmese, 4395tc 0.12 45 含量x(%)有关。为研究两个变量间的关 0.13 45 0.14 45 系。首先是收集数据,我们把收集到的 0.15 47.5 数据记为(x,y),i=1,2,.,n。本例中,我们 0.16 49 0.17 53 收集到12组数据,列于表中 0.18 50 0.2 55 0.21 55 0.23 60 School of Microelectronics and Solid-State Electronics 11
School of Microelectronics and Solid-State Electronics 11 第五章 回归分析方法 例1 合金的强度y (×107 Pa) 与合金中碳的 含量x (%) 有关。为研究两个变量间的关 系。首先是收集数据,我们把收集到的 数据记为(xi ,yi ),i=1,2,,n。本例中,我们 收集到12组数据,列于表中 进行回归分析首先是回归函数形式的选择。 当只有一个自变量时,通常可采用画散点图 的方法进行选择。 0.1 42 0.11 43 0.12 45 0.13 45 0.14 45 0.15 47.5 0.16 49 0.17 53 0.18 50 0.2 55 0.21 55 0.23 60
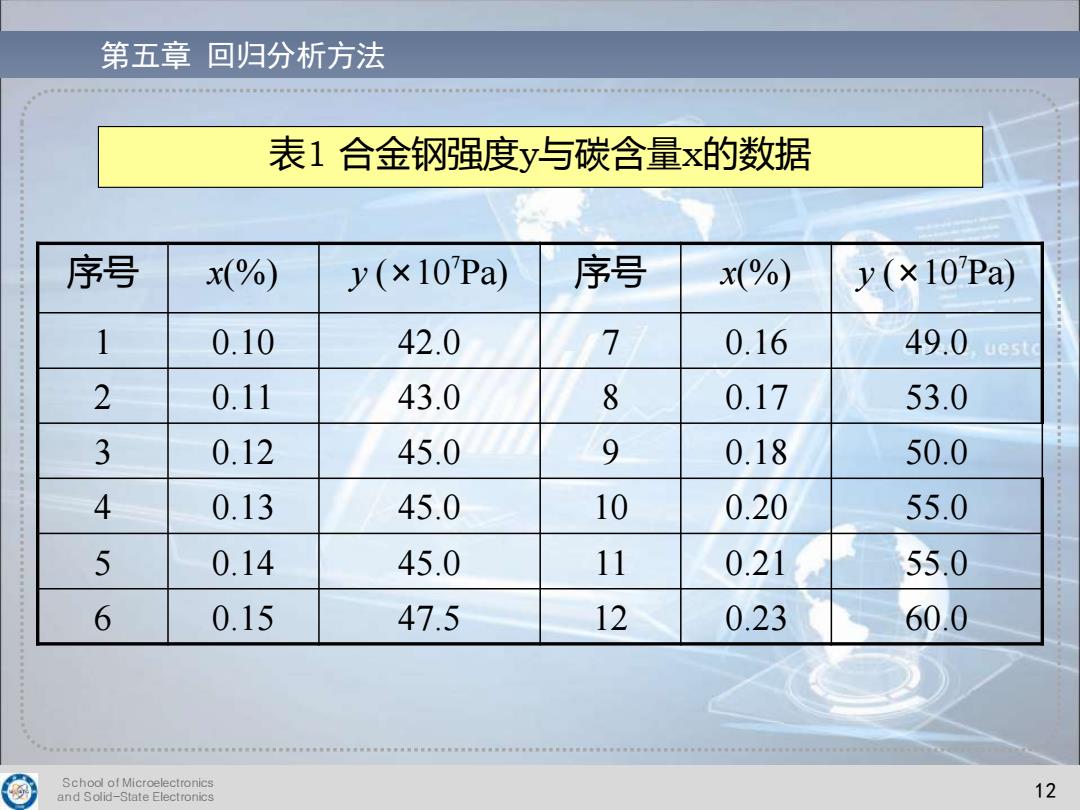
第五章回归分析方法 表1合金钢强度y与碳含量x的数据 序号 x(%) y(×10Pa) 序号 x(%) y(×10Pa) 1 0.10 42.0 7 0.16 49.0 uesto 2 0.11 43.0 8 0.17 53.0 3 0.12 45.0 9 0.18 50.0 4 0.13 45.0 10 0.20 55.0 5 0.14 45.0 11 0.21 55.0 6 0.15 47.5 12 0.23 60.0 School of Microelectronics and Solid-State Electronics 12
School of Microelectronics and Solid-State Electronics 12 第五章 回归分析方法 表1 合金钢强度y与碳含量x的数据 序号 x(%) y (×107 Pa) 序号 x(%) y (×107 Pa) 1 0.10 42.0 7 0.16 49.0 2 0.11 43.0 8 0.17 53.0 3 0.12 45.0 9 0.18 50.0 4 0.13 45.0 10 0.20 55.0 5 0.14 45.0 11 0.21 55.0 6 0.15 47.5 12 0.23 60.0

第五章 回归分析方法 为找出两个量间存在的 回归函数的形式,可以 60 画一张图:把每一对数 剑 50 (x,y)看成直角坐标系中 的一个点,在图上画出n 0.10 0.1 0.20 个点,称这张图为散点 碳含量 合金钢强度及碳含量的散点图 图,见图。 School of Microelectronics and Solid-State Electronics 13
School of Microelectronics and Solid-State Electronics 13 第五章 回归分析方法 为找出两个量间存在的 回归函数的形式,可以 画一张图:把每一对数 (xi ,yi)看成直角坐标系中 的一个点,在图上画出n 个点,称这张图为散点 图,见图。 0.10 0.15 0.20 40 50 60 碳含量 合 金 钢 强 度 合金钢强度及碳含量的散点图

第五章回归分析方法 从散点图我们发现12个点基本在一条直线附近,这说 明两个变量之间有一个线性相关关系,这个相关关系 可以表示为 y=Bo+Bx+8 (1) uestc 这便是y关于x的一元线性回归的数据结构式。通常假定 E(8=0,Var(8=o2 (2) 在对未知参数作区间估计或假设检验时,还需要假定误 差服从正态分布,即 yN(B。+Bx,o2) (3) 显然,假定(3)比(2)要强。 School of Microelectronics and Solid-State Electronics 14
School of Microelectronics and Solid-State Electronics 14 第五章 回归分析方法 从散点图我们发现12个点基本在一条直线附近,这说 明两个变量之间有一个线性相关关系,这个相关关系 可以表示为 y = 0+ 1x + (1) 这便是y关于x的一元线性回归的数据结构式。通常假定 E() =0, Var() = 2 (2) 在对未知参数作区间估计或假设检验时,还需要假定误 差服从正态分布,即 y ~N(0+ 1x, 2 ) (3) 显然,假定(3) 比 (2) 要强

第五章 回归分析方法 由于B,B均未知,需要我们从收集到的数 据(x,y,i=1,2,,n,出发进行估计。在收 集数据时,我们一般要求观察独立地进行 即假定y,y.,y相互独立。综合上述 诸项假定,我们可以给出最简单、常用的 一元线性回归的数学模型: y=B+Bx,+,i=1,2,…n 各ε,独立同分布,其分布为N(0,σ2) (4) School of Microelectronics and Solid-State Electronics 15
School of Microelectronics and Solid-State Electronics 15 第五章 回归分析方法 由于0 , 1均未知,需要我们从收集到的数 据(xi ,yi),i=1,2,…,n,出发进行估计。在收 集数据时,我们一般要求观察独立地进行 ,即假定y1 , y2 ,, yn ,相互独立。综合上述 诸项假定,我们可以给出最简单、常用的 一元线性回归的数学模型: (4) 0 1 2 1,2, (0, ) i i i i y x i n N = + + = , 各 独立同分布,其分布为