
例1求解二元线性方程组3x-2x2=12,2x +x =1.3-2解D==3-(-4)=7±0211212.22-21,D14,D,三21D1421D,-3.2X1X27DD7
例 1 + = − = 2 1. 3 2 12, 1 2 1 2 x x x x 求解二元线性方程组 解 2 1 3 − 2 D = = 3 − ( − 4 ) = 7 0 , 1 1 12 2 1 − D = = 14 , 2 1 3 12 D 2 = = −21 , DD x 1 1 = 2 , 7 14 = = DD x 2 2 = 3. 7 21 = − − =

类似地,ax +aX, +aix = bi由三元线性方程组a21x, +a22x +a23g =b2, (1-2)a31xi+a32x+a33=b;引入记号a13222(23a21a3231(33称之为三阶行列式
引入记号 称之为三阶行列式. 由三元线性方程组 11 1 12 2 13 3 1 21 1 22 2 23 3 2 31 1 32 2 33 3 3 , , 1 2 ; a x a x a x b a x a x a x b a x a x a x b + + = + + = − + + = ( ) 11 12 13 21 22 23 31 32 33 a a a a a a a a a 类似地

b,113a123a记D,=1b25D=0sb3132a33133bia11a13bianla12b2D21a21a23b2D=a22a21b3a33a31b3a32a31则当系数行列式不为零时,三元线性方程组的解为DiD2D3X1X2X3DDD
, 31 3 33 21 2 23 11 1 13 2 a b a a b a a b a D = . 31 32 3 21 22 2 11 12 1 3 a a b a a b a a b D = 则当系数行列式不为零时,三元线性方程组的解为: , 1 1 D D x = , 2 2 D D x = . 3 3 D D x = 记 11 12 13 21 22 23 31 32 33 a a a D a a a a a a = 1 12 13 1 2 22 23 3 32 33 b a a D b a a b a a =
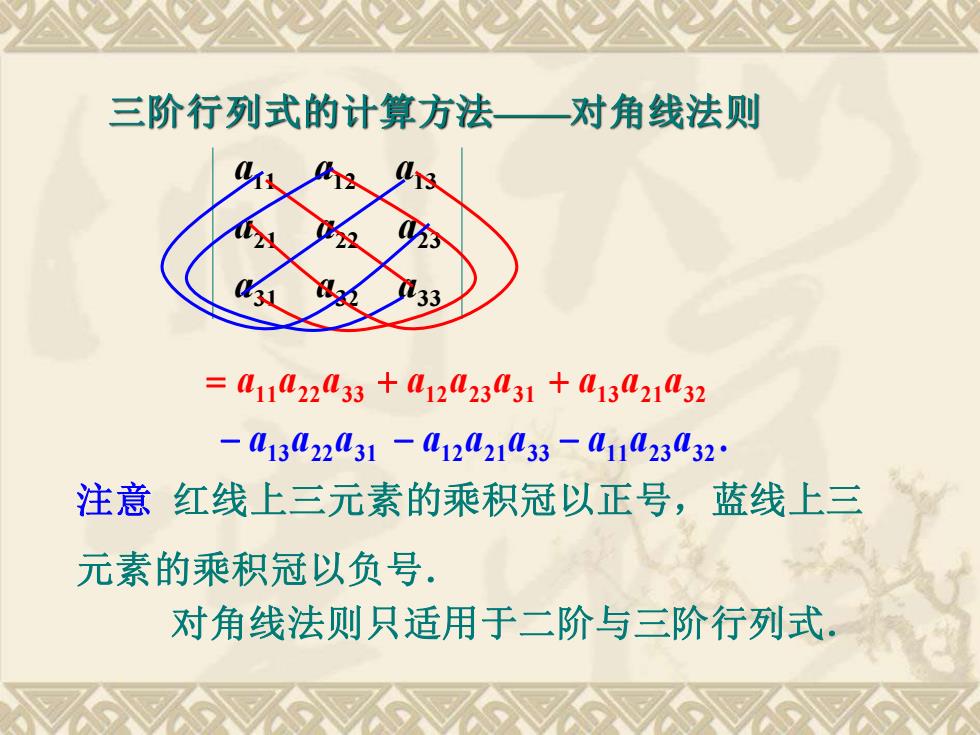
三阶行列式的计算方法一对角线法则33= a11a22a33 + a12a23a31 +132132a13A22431 —a122133 -a12332注意红线上三元素的乘积冠以正号,蓝线上三元素的乘积冠以负号对角线法则只适用于二阶与三阶行列式
31 32 33 21 22 23 11 12 13 a a a a a a a a a 11 22 33 = a a a . 11 23 32 − a a a 三阶行列式的计算方法——对角线法则 注意 红线上三元素的乘积冠以正号,蓝线上三 元素的乘积冠以负号. 对角线法则只适用于二阶与三阶行列式. 13 21 32 + a a a 12 23 31 + a a a 13 22 31 − a a a 12 21 33 − a a a

124例2计算三阶行列式D=-23-2解按对角线法则,有D = 1×2 ×(-2)+ 2 ×1×(-3)+(-4)×(-2) ×4-(-4)×2 ×(-3) -1×1×4 - 2×(-2)×(-2)=-4-6+32-24-4-8=-14
1 2 4 2 2 1 3 4 2 D = - 计算三阶行列式 - - - 例2 解 按对角线法则,有 D = 1 2(−2) + 21(−3) + (−4)(−2) 4 − − − − − − − ( 4) 2 ( 3) 1 1 4 2 ( 2) ( 2) = − − + − − − 4 6 32 24 4 8 = −14