
概率的性质 5、对任意事件A,有P(A)≤1. 证明因Ac2,由性质4得P(A)≤P(2)=1. 6、加法公式:对任意的事件A,B有 P(AUB)=P(A)+P(B)-P(AB). 特别地,若A与B互斥,则有P(AUB)=P()+P(B). 证明因为AUB=AU(B-AB)且A∩(B-AB=Φ, ABCB,所以 P(AUB)=P(A)+P(B-AB)=P(A)+P(B)-P(AB). 2024年8月27日星期二 17 目录今 上页> 下页 返回
2024年8月27日星期二 17 目录 上页 下页 返回 概率的性质 5、对任意事件 A ,有 P A( ) 1 . 证明 因 A ,由性质 4 得 P A P ( ) ( ) 1. = 6、加法公式:对任意的事件 A B, 有 P A B ( ) = P A P B P AB ( ) ( ) ( ) + − . 特别地,若 A 与 B 互斥,则有P A B P A P B ( ) ( ) ( ) = + . 证 明 因 为 A B A B AB A B AB = − − ( )且 ( )= , AB B ,所以 P A B P A P B AB ( ) ( ) ( ) = + − =P A P B P AB ( ) ( ) ( ) + − .

推广 设A,A,.,An是任意n个事件,则有 P(AUA,U.UA,)=∑P(A)-∑P(AA) i=1 1≤i<j≤n +∑P(AAA)+.+(-1)P(AA.A,) lsi<j<k≤n 特别地,有 P(AUBUC)=P(A)+P(B)+P(C) -P(AB)-P(AC)-P(BC)+P(ABC) 2024年8月27日星期二 18 目录) 上页 下页 返回
2024年8月27日星期二 18 目录 上页 下页 返回 推广 设 1 2 , , , A A A n 是任意 n 个事件,则有 1 2 1 1 ( ) ( ) ( ) n n i i j i i j n P A A A P A P A A = = − 1 1 2 1 ( ) ( 1) ( ) n i j k n i j k n P A A A P A A A + + + + − . 特别地,有 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) P A B C P A P B P C −−−−−−− P AB P AC P BC P ABC = + + − − − − +

【例3】小王参加“智力大冲浪”游戏,他能答出甲、 乙两类问题的概率分别为0.7和0.2,两类问题都能答 出的概率为0.1.求小王 (1)答出甲类而答不出乙类问题的概率; (2)至少有一类问题能答出的概率; (3)两类问题都答不出的概率; (4)至少一类问题答不出的概率. 解设事件A,B分别表示“能答出甲、乙类问题”,则 P(A)=0.7,P(B)=0.2,P(AB)=0.1,所以有 (1)P(AB)=P(A)-P(AB)=0.7-0.1=0.6; (2)P(AUB)=P(A)+P(B)-P(AB)=0.7+0.2-0.1=0.8; (3)P(AB)=P(AUB)=1-P(AUB=1-0.8=0.2; (4)P(AUB)=P(AB)=1-P(AB)=1-0.1=0.9. 2024年8月27日星期二 19 目录 上页 下页 返回
2024年8月27日星期二 19 目录 上页 下页 返回 【例 3】小王参加“智力大冲浪”游戏,他能答出甲、 乙两类问题的概率分别为 0.7 和 0.2,两类问题都能答 出的概率为 0.1.求小王 (1) 答出甲类而答不出乙类问题的概率; (2) 至少有一类问题能答出的概率; (3) 两类问题都答不出的概率; (4) 至少一类问题答不出的概率. 解 设事件 A B, 分别表示“能答出甲、乙类问题”,则 P A( ) 0.7 = , P B( ) 0.2 = , P AB ( ) 0.1 = ,所以有 (1) P AB P A P AB ( ) ( ) ( ) 0.7 0.1 0.6 = − = − = ; (2) P A B P A P B P AB ( ) ( ) ( ) ( ) 0.7 0.2 0.1 0.8 = + − = + − = ; (3) P A B P A B P A B ( ) ( ) 1 0.2 = = − = ( )= 1- 0.8 ; (4) P A B P AB P AB ( ) ( ) 1 ( ) 1 0.1 0.9 = = − = − =

【例4】己知P0=)=PO,P0)=0, P4CO)=P(BC)号:则事件ARC全不发生的概率为 多少? 解P(ABC)=1-P(AUBUC) =1-P(A-P(B)-P(C) +P(AB)+P(AC)+P(BC)-P(ABC) =1-1-1101, -+0+ 1-0 4449 17 36 2024年8月27日星期二 20 目录○ 上页 下页 返回
2024年8月27日星期二 20 目录 上页 下页 返回 【 例 4】已 知 P A( ) = P B( ) = 1 ( ) 4 P C = , P AB ( ) = 0, P AC ( ) = 1 ( ) 9 P BC = .则事件 A、B、C 全不发生的概率为 多少? 解 P A BC P A B C ( ) 1 ( ) = − = − − − 1 ( ) ( ) ( ) P A P B P C + + + − P AB P AC P BC P ABC ( ) ( ) ( ) ( ) 1 1 1 1 1 1 0 0 4 4 4 9 9 = − − − + + + − 17 . 36 =
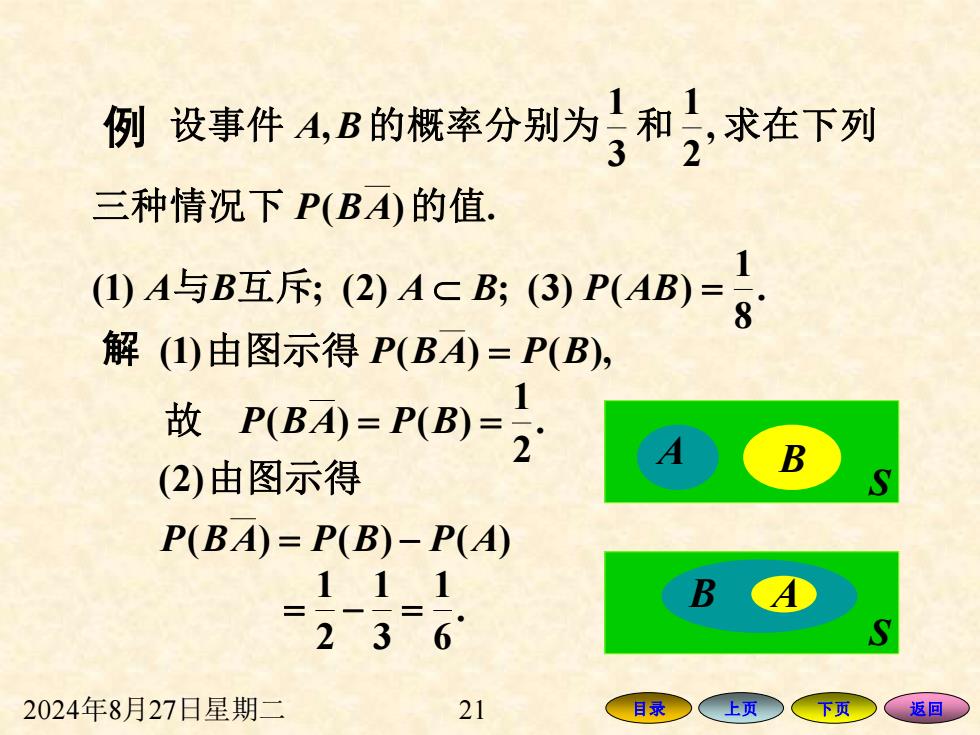
例设事件48的概率分别为}和2求在下列 三种情况下P(BA)的值. 四A写B互斥:2)ACB③)PAB)= 解()由图示得P(B)=P(B), 故P(BA=P(B=2 1 (2)由图示得 B P(BA)=P(B)-P(A) 111 D 236 2024年8月27日星期二 21 目录○ 上页下页 返回
2024年8月27日星期二 21 目录 上页 下页 返回 解 (1)由图示得 P(BA) = P(B), . 2 1 故 P(BA) = P(B) = ( ) ( ) ( ) (2) P BA = P B − P A 由图示得 . 6 1 3 1 2 1 = − = . 8 1 (1) ; (2) ; (3) ( ) ( ) . , 2 1 3 1 , A B A B P AB = P BA A B 与 互斥 三种情况下 的值 设事件 的概率分别为 和 求在下列 B A S S A B 例