例10.4的图和方程 对杆件1, ∑X=0Nax+Ncx=O; ΣY=0Nay+Ncy-Gl=0; EM=Ncy*Ll*cos(thetal)-Ncx*Ll*sin(thetal)-G1*L1/2*cos(thetal)=0; 对杆件2 ΣX=0Nbx-Ncx=0; ΣY=0Nby-Ncy-G2=0; EM=Ncy*L2*cos (theta2)+Ncx*L2*sin(theta2)+G2*L2/2*cos(theta2)=0;
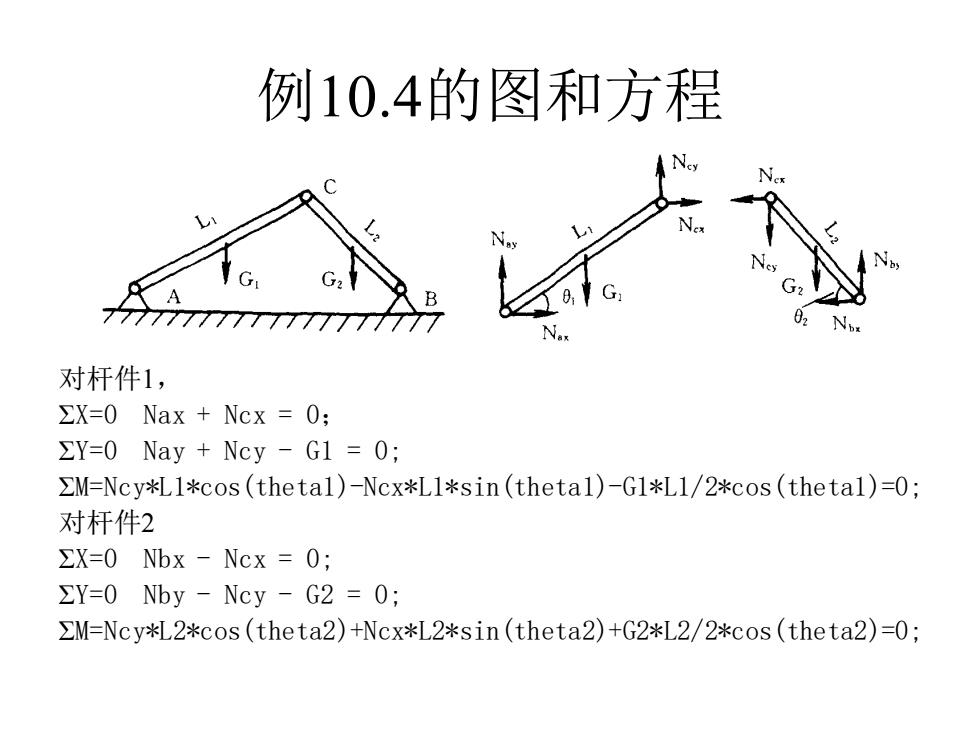
例10.4的图和方程 对杆件1, ΣX=0 Nax + Ncx = 0; ΣY=0 Nay + Ncy - G1 = 0; ΣM=Ncy*L1*cos(theta1)-Ncx*L1*sin(theta1)-G1*L1/2*cos(theta1)=0; 对杆件2 ΣX=0 Nbx - Ncx = 0; ΣY=0 Nby - Ncy - G2 = 0; ΣM=Ncy*L2*cos(theta2)+Ncx*L2*sin(theta2)+G2*L2/2*cos(theta2)=0;

例10.4的矩阵模型 这是一组包含六个未知数Nax,Nay,Nbx,Nby,Ncx,Ncy的六个 线性代数方程,写成矩阵方程AX+B,其中 10001 0 0 Nax 0100 0 1 Gj Nay 0 000 L sin L.cos G L cos0/2 Nbx A= ,B= ,X= 0010-1 0 0 Nby 0001 0 -1 G2 Ncx 0000 Lzsine L2cos2 -G,L,c0s0,/2 Ncy A=[1,0,0,0,1,0;0,1,0,0,0,10,0,0,0,-sin(thetal) cos(theta1)0,0,1,0,-1,0,0,0,0,1,0,-1;0,0,0,0,… sin(theta2),cos(theta2)]; B=[0;G1;G1/2*cos(thetal);0;G2;-G2/2*cos(theta2)]; ·X=AB %求解线性方程组
例10.4的矩阵模型 • 这是一组包含六个未知数Nax, Nay, Nbx, Nby, Ncx, Ncy的六个 线性代数方程,写成矩阵方程AX+B,其中 A=[1,0,0,0,1,0;0,1,0,0,0,1;0,0,0,0,-sin(theta1),... cos(theta1);0,0,1,0,-1,0;0,0,0,1,0,-1;0,0,0,0,... sin(theta2),cos(theta2)]; • B=[0; G1; G1/2*cos(theta1); 0; G2; -G2/2*cos(theta2)]; • X = A\B % 求解线性方程组 1 1 1 1 2 1 0 0 0 1 0 0 1 0 0 0 1 0 0 0 0 L sin L cos 0 0 1 0 -1 0 0 0 0 1 0 -1 0 0 0 0 L sin A = 1 1 1 1 2 2 2 2 2 2 2 0 Nax G Nay G L cos / 2 Nbx , , 0 Nby G Ncx L cos Ncy -G L cos / 2 = = B X

程序ag1004的运行结果 Nax 95.0962 。 这样求解的方 Nay 154.9038 法不仅适用于 全部静力学题 Nbx -95.0962 X= 目,而且可用 Nby 145.0962 于材料力学和 Nex -95.0962 结构力学中的 Ney 45.0962 静力学和静不 定问题
程序ag1004的运行结果 • 这样求解的方 法不仅适用于 全部静力学题 目,而且可用 于材料力学和 结构力学中的 静力学和静不 定问题。 95.0962 154.9038 -95.0962 145.0962 -95.0962 45.0962 Nax Nay Nbx Nby Nex Ney = = X
10.5材料力学的静不定问题 。 建模:A点因各杆变形而引起 的x方向位移△x,y方向位移 △y,由几何关系,得变形方程: = N=Axcosa,+△yin&i=l,…,m) 其中K为杆的刚度系数。再 加上两个力平衡方程: ,cosPcos ∑N,sina,=Psina 共有+2个方程,其中包含n 个未知力和两个待求位移△x 和△y,方程组适定可解
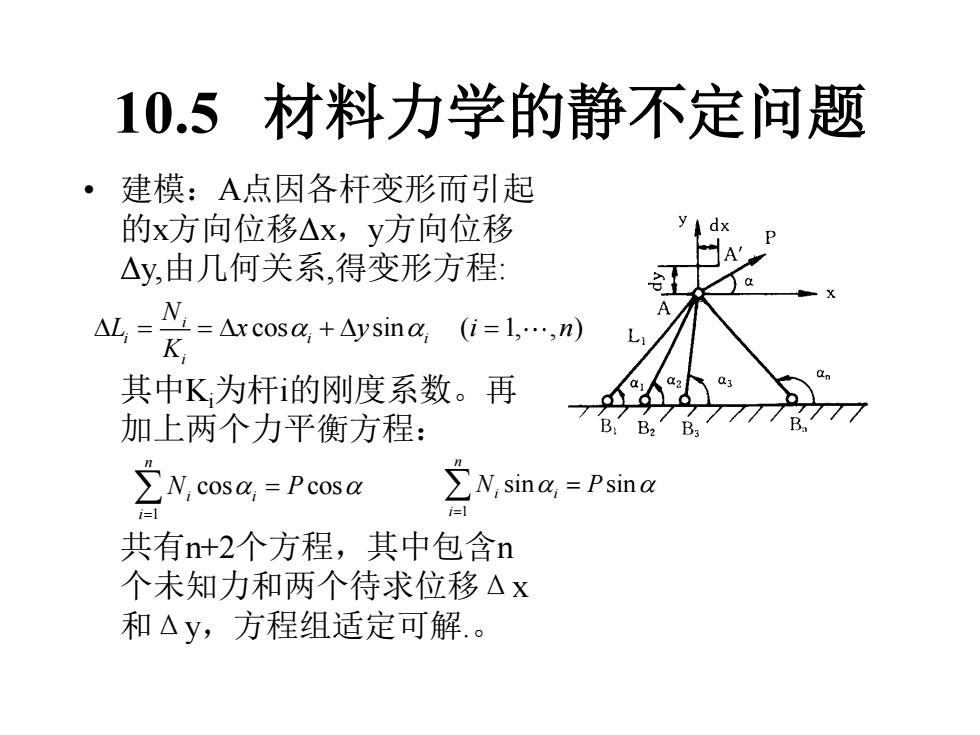
10.5 材料力学的静不定问题 • 建模:A点因各杆变形而引起 的x方向位移Δx,y方向位移 Δy,由几何关系,得变形方程: 其中Ki为杆i的刚度系数。再 加上两个力平衡方程: 共有n+2个方程,其中包含n 个未知力和两个待求位移Δx 和Δy,方程组适定可解.。 cos sin ( 1, , ) i i i i i N L x y i n K = = + = 1 cos cos n i i i N P = = 1 sin sin n i i i N P = =

例10.5三杆静不定桁架 图示三杆桁架,挂一重物P=3000,设 L=2m,各杆的截面积分别为A1=200e- 6,A2=300e-6,A3=400e-6,材料的弹性 模量E=200e9,求各杆受力的大小。 解:此时应有两个平衡方程和三个位移 协调方程 -N1*cos(a1)-N2-N3*cos(a3)=0; N1*sin (a1)-N3*sin (a3)=P; N1/K1=dx*cos (al)+dy*sin(a1) N2/K2 dx N3/K3=dx*cos (a3)-dy*sin(a3)
例10.5 三杆静不定桁架 图示三杆桁架,挂一重物P=3000,设 L=2m,各杆的截面积分别为A1=200e- 6, A2=300e-6, A3=400e-6, 材料的弹性 模量E=200e9,求各杆受力的大小。 解:此时应有两个平衡方程和三个位移 协调方程: -N1*cos(a1)-N2-N3*cos(a3)=0; N1*sin(a1)-N3*sin(a3)=P; N1/K1=dx*cos(a1)+dy*sin(a1) N2/K2 = dx N3/K3=dx*cos(a3)–dy*sin(a3)