按圆形估计的最小二乘图形 -66.06 1 18.1809 -47.80 1 19.2100 -2 8.70 1 C) 19.9225 0 9.00 1 20.2500 2 8.80 1 C3 20.3600 001018+-049932160153=0 4 8.04 20.1604 6 6.52 1 19.6276 AX=B 以上就是本题要解的超定线性方程组 ·快速绘制此圆形的语句为: ezplot'(x-0.1018)2+(y-0.4996)2-4.00172=0')
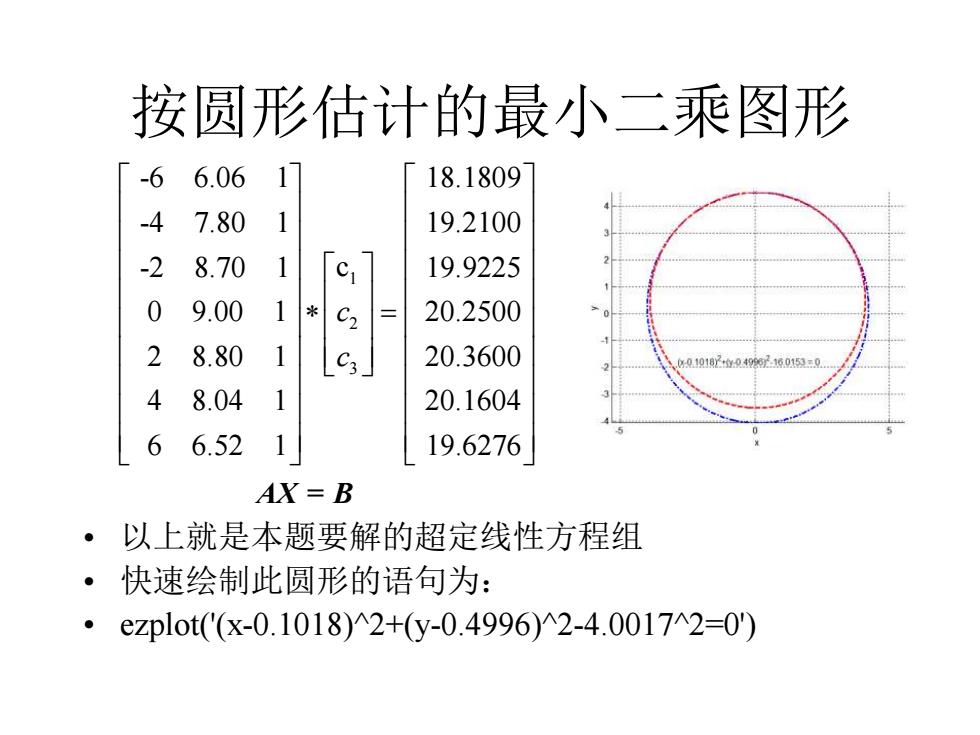
按圆形估计的最小二乘图形 • 以上就是本题要解的超定线性方程组 • 快速绘制此圆形的语句为: • ezplot('(x-0.1018)^2+(y-0.4996)^2-4.0017^2=0') 1 2 3 -6 6.06 1 18.1809 -4 7.80 1 19.2100 -2 8.70 1 19.9225 c 0 9.00 1 20.2500 2 8.80 1 20.3600 4 8.04 1 20.1604 6 6.52 1 c c = 19.6276 AX = B

10.3天体轨道测量拟合 在适当的极坐标中,天体的位置应满足下列方程: r=B+(r·cosO) ·其中B为常数而ε是轨道的偏心率,对于椭圆,对于抛 物线,而对于双曲线。对一个新发现的天体的观测得 到了表中的数据,试确定其轨道的性质,并预测此天 体在弧度时的位置。 0.88 1.10 1.42 1.77 2.14 r 3.00 2.30 1.65 1.25 1.01 ·解:对任何一组测量数据0, 可列出以下对B和ε两个 变量的线性方程:
10.3 天体轨道测量拟合 在适当的极坐标中,天体的位置应满足下列方程: • 其中β为常数而ε是轨道的偏心率,对于椭圆,对于抛 物线,而对于双曲线。对一个新发现的天体的观测得 到了表中的数据,试确定其轨道的性质,并预测此天 体在弧度时的位置。 • 解:对任何一组测量数据θi ,ri,可列出以下对β和ε两个 变量的线性方程: r r = + ( cos ) 0.88 1.10 1.42 1.77 2.14 3.00 2.30 1.65 1.25 1.01 0 r θ

求B和ε的程序 五个测量点共有五个方程,轨道只有两个未知数,这 是一个超定问题。先用元素群运算一次列出5个方程的 系数矩阵,再用超定方程解的公式。 theta-=[0.88,1.1,1.42,1.77,2.14]',%测定的theta和r数组 r=[3,2.3,1.65,1.25,1.01]° A=[ones(5,l),r.*cos(theta)儿,B=r,%方程组系数矩阵 X=inv(A*A)*A?*B%解超定方程 rg=X(1)/(1-X(2)*cos(0.46)%求theta=0.46处的r 运行结果为: 即轨道方程为 r=1.4509/1-0.8111cos0),g=5.3098
求β和ε的程序 • 五个测量点共有五个方程,轨道只有两个未知数,这 是一个超定问题。先用元素群运算一次列出5个方程的 系数矩阵,再用超定方程解的公式。 theta=[0.88,1.1,1.42,1.77,2.14]'; % 测定的theta 和r 数组 r =[3, 2.3, 1.65, 1.25, 1.01]‘ A=[ ones(5,1), r.*cos(theta)], B=r, % 方程组系数矩阵 X=inv(A‘*A)*A’*B % 解超定方程 rg=X(1)/(1-X(2)*cos(0.46)) % 求theta=0.46处的r 运行结果为: • 即轨道方程为 ,rg=5.3098 1.4509 0.8111 X = = r = − 1.4509 /(1 0.8111 cos )

程序agl002a的数据和图形 1.0000 1.9115 3.0000 1.0000 1.0433 2.3000 1.0000 0.2479 1.6500 1.0000 -0.2474 1.2500 1.0000 -0.5444 1.0100 AX=B %画出极坐标中轨迹的语句, ezpolar('1.4509/(1-0.8111*cos(theta)月, hold on,polar(theta,r,'x),axis([-4,8,-5,5]) %画出测定点 得到图形如右
程序ag1002a的数据和图形 % 画出极坐标中轨迹的语句, ezpolar('1.4509/(1-0.8111*cos(theta))'), hold on,polar(theta, r,'x'), axis([-4,8,-5,5]) %画出测定点 得到图形如右。 1.0000 1.9115 3.0000 1.0000 1.0433 2.3000 1.0000 0.2479 1.6500 1.0000 -0.2474 1.2500 1.0000 -0.5444 1.0100 = AX = B

10.4静力学问题 ·静力学研究物体受力后的平衡方程。一个物体在平面 上平衡,需要三个平衡方程。如果是N个物体相互作用 下的平衡,那么方程的总数就是3N个。空间物体的平 衡需要6个平衡方程。这个方程组通常都是线性的,所 以求解就可以归结为矩阵方程。它可以避免解单个方 程和单个数,只要把系数矩阵输入程序,就轻而易举 地同时得出所有的解。 例10.4两杆系统受力图见图,设已知:G1=200: G2=100;L1=2,L2=sqrt(2);thetal=30*pi/180; theta2 =45*pi/180; ·求所示杆系的支撑反力Na,Nb,Nco
10.4 静力学问题 • 静力学研究物体受力后的平衡方程。一个物体在平面 上平衡,需要三个平衡方程。如果是N个物体相互作用 下的平衡,那么方程的总数就是3N个。空间物体的平 衡需要6个平衡方程。这个方程组通常都是线性的,所 以求解就可以归结为矩阵方程。它可以避免解单个方 程和单个数,只要把系数矩阵输入程序,就轻而易举 地同时得出所有的解。 • 例10.4 两杆系统受力图见图,设已知:G1=200; G2=100; L1= 2; L2=sqrt(2); theta1 =30*pi/180; theta2 = 45*pi/180; • 求所示杆系的支撑反力Na,Nb,Nc