
4.2平面机构的运动分析 pc代表了C点的加速度ac、bc代表acB,大小分别为 ac ua x p'c' acB=H×bc (3)求a2、a3由图4.1c可知,c”C 代表dsc"c代表a心 将它们平移到机构图中的C点处,可得 a=%'c”c 逆时针方向 a Ma xc'c' 逆时针方向
4.2 平面机构的运动分析 p c 代表了C点的加速度aC、 b c 代表aCB,大小分别为 a p c C a = a b c CB a = (3)求a2、a3由图4.1c可知, c c 代表 t CB a c c , 代表 t C a 将它们平移到机构图中的C点处,可得 BC a l c c a = 2 逆时针方向 CD a l c c a = 3 逆时针方向

4.2平面机构的运动分析 (4)求aE因为B、C、E是同一构件上的三点,可列出下列方程式 =aB +ape +aeB =ac +arc asc 大小 Hap'b' @leB 。·pc @lec ? 方向 p'→b E→B ⊥EBp'→c EC⊥EC 如图4.1c所示,过b点作be'∥EB,方向从E→R,长度为be=2 Ma 再过e"点作d的方向线e”e;同样过c'点作ce”代表aEB,再作 e”作ac的方向线e"e,与aEB的方向线相交于e'点。这样矢量 pe代表aE,矢量be代表Aec,大小分别为 aE=h,×p'eaeB=4nxb'e aEc ua xc'e
4.2 平面机构的运动分析 (4)求aE因为B、C、E是同一构件上的三点,可列出下列方程式 E a t EC = aB + a n + aEB t + aEB C = a n EC + a 大小 方向 ? ? a p b p → b EB l 2 2 E→B ? ⊥EB p c a p → c EC l 2 2 E →C ? ⊥EC 如图4.1c所示,过b′点作 b e // EB ,方向从E→B,长度为 a n aEB b e = 再过e″点作 t EB a 的方向线 e e ;同样过c′点作 c e 代表 n EB a ,再作 e 作 t EC a 的方向线 e e ,与 t EB a 的方向线相交于e′点。这样矢量 p e 代表aE,矢量 b e 代表Aec,大小分别为 a p e E a = a b e EB a = a c e EC a =
4.2平面机构的运动分析 4.2.2组成移动副的两构件瞬时重合点的速度、加速度分析 已知条件: 机构的位置 各构件的长度 主动件1以等角速度01 b() 顺时针转动 要求: 试求导杆3的角速度03 角加速度C3
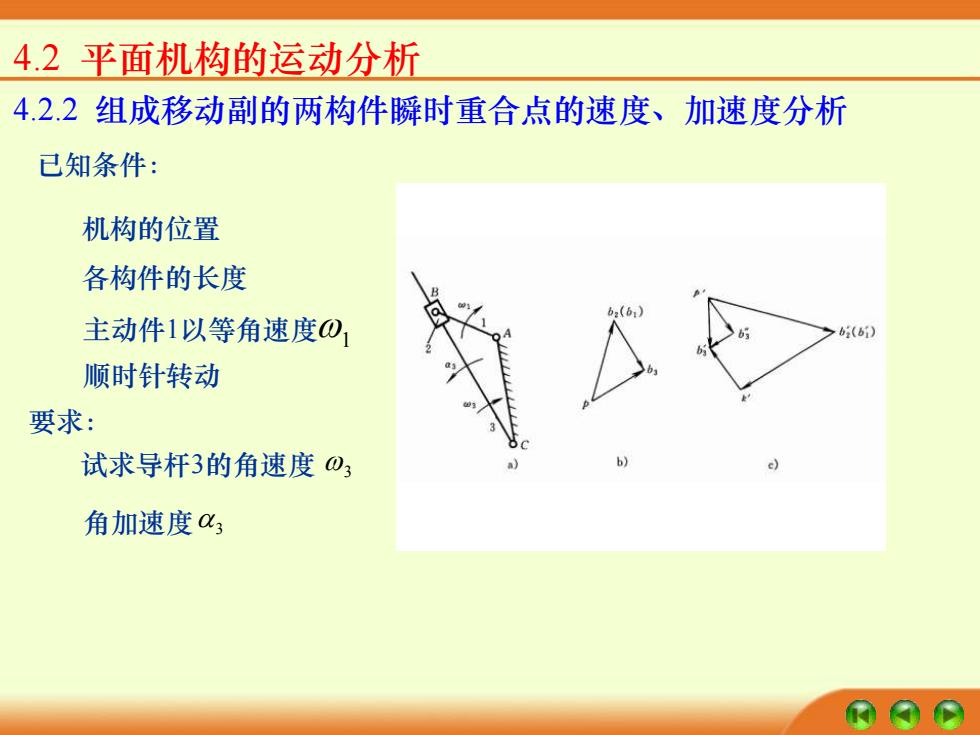
4.2 平面机构的运动分析 4.2.2 组成移动副的两构件瞬时重合点的速度、加速度分析 已知条件: 要求: 机构的位置 各构件的长度 1 顺时针转动 主动件1以等角速度 试求导杆3的角速度 3 角加速度 3

4.2平面机构的运动分析 1速度分析 (1)求VB, 构件1和构件2在B点组成转动副,所以,VB,=VB=O·14B 方向垂直于AB,指向与O1的方向相同。 (2)求VB, 构件2和构件3组成移动副,B2与B3为瞬时重合点。由理论 力学可知,B3点的绝对速度等于与其重合的牵连点B的绝 对速度和B3相对于B2的相对速度的合成,即 二VB +VB3B2 大小 OLAB 方向 ⊥AB ⊥AB //BC 该式只有两个未知数,可用图解法求解。如图4.2b所示,选定速度比 m/s 例尺山, mm
4.2 平面机构的运动分析 1.速度分析 (1)求 B2 v 构件1和构件2在B点组成转动副,所以, B B AB v = v = l 2 1 1 方向垂直于AB,指向与 1 的方向相同。 (2)求 B3 v 构件2和构件3组成移动副,B2与B3为瞬时重合点。由理论 力学可知,B3点的绝对速度等于与其重合的牵连点B2的绝 对速度和B3相对于B2的相对速度的合成,即 B2 = v B3 v B3 B2 + v 大小 方向 ? ⊥AB AB l 1 ⊥ AB ? //BC 该式只有两个未知数,可用图解法求解。如图4.2b所示,选定速度比 例尺 mm m /s v
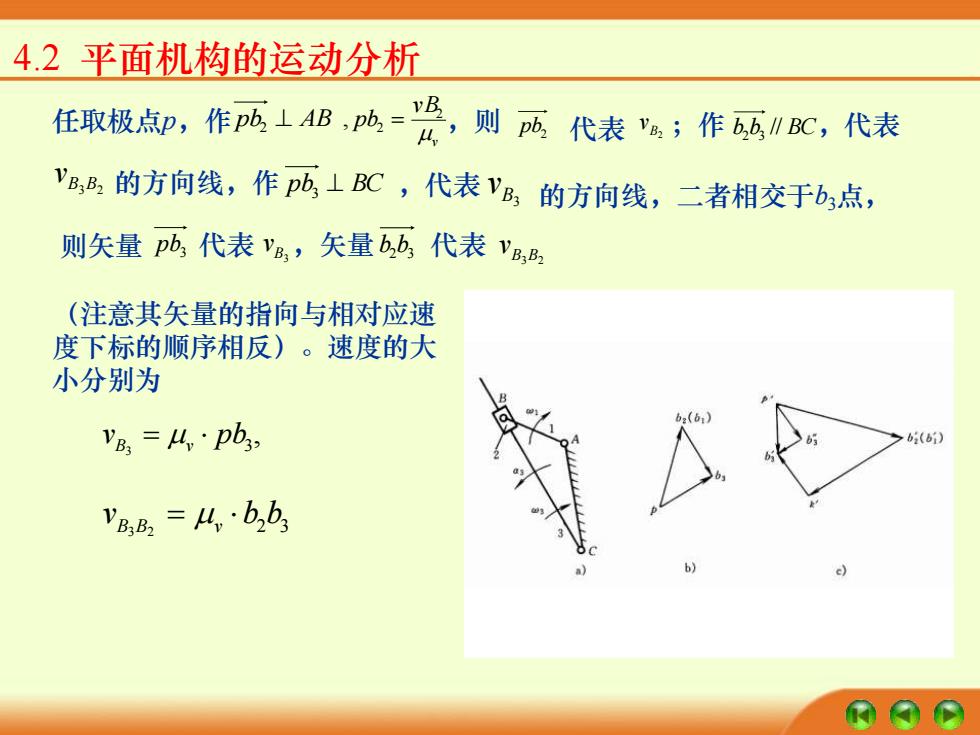
4.2平面机构的运动分析 任取极点,作西上B,鸣-发,则西代表%;作,代表 VB,B的方向线,作b⊥BC,代表VB,的方向线,二者相交于b3点, 则失量pb代表yg,矢量b,6代表V, (注意其矢量的指向与相对应速 度下标的顺序相反)。速度的大 小分别为 VB,=4,·pb, bi(6) VB,B2=4,·bb
4.2 平面机构的运动分析 任取极点p,作 pb2 ⊥ AB v vB pb 2 2 , = ,则 pb2 代表 B2 v ;作 b2 b3 // BC ,代表 B3 B2 v 的方向线,作 pb3 ⊥ BC ,代表 B3 v 的方向线,二者相交于b3点, 3 pb 代表 B3 v ,矢量 2 3 b b 代表 B3 B2 则矢量 v (注意其矢量的指向与相对应速 度下标的顺序相反)。速度的大 小分别为 , 3 pb3 vB v = 3 2 b2 b3 vB B v =