
4.2平面机构的运动分析 2.加速度分析 (1)求0B2 aB,=AB,其大小为aB,=O1AB,方向为B-→M。 (2)求aB, 由理论力学可知,B3点的绝对加速度aB,等于牵连加速度ag, 哥氏加速度g,B,和相对加速度4g,的合成,其中哥氏加 速度的大小aB,=2OYa,B,方向由相对速度VB,B2 的指向顺着牵连角速度02转过90°而得,即 +aB, 二aB2 +aB;B 大小 @lrc 2 OIAB di,=20.'a,a 方向 B→C ⊥BCA→B ⊥BC lBC
4.2 平面机构的运动分析 2.加速度分析 B2 (1)求 a = B2 a B1 a ,其大小为 B AB a l 2 2 =1 ,方向为B→A。 (2)求 B3 a 由理论力学可知,B3点的绝对加速度 B3 a 等于牵连加速度 B2 a 哥氏加速度 k aB3 B2 和相对加速度 r aB3 B2 的合成,其中哥氏加 3 2 2 3 2 2 B B k B B a = v ,方向由相对速度 B3 B2 速度的大小 v 的指向顺着牵连角速度 2 转过90°而得,即 n B a 3 t aB3 + B2 = a k aB3 B2 + r aB3 B2 + 大小 方向 BC l 2 3 B →C ? ⊥BC AB l 2 1 A→ B 3 2 2 3 2 2 B B k B B a = v ⊥ BC ? //BC
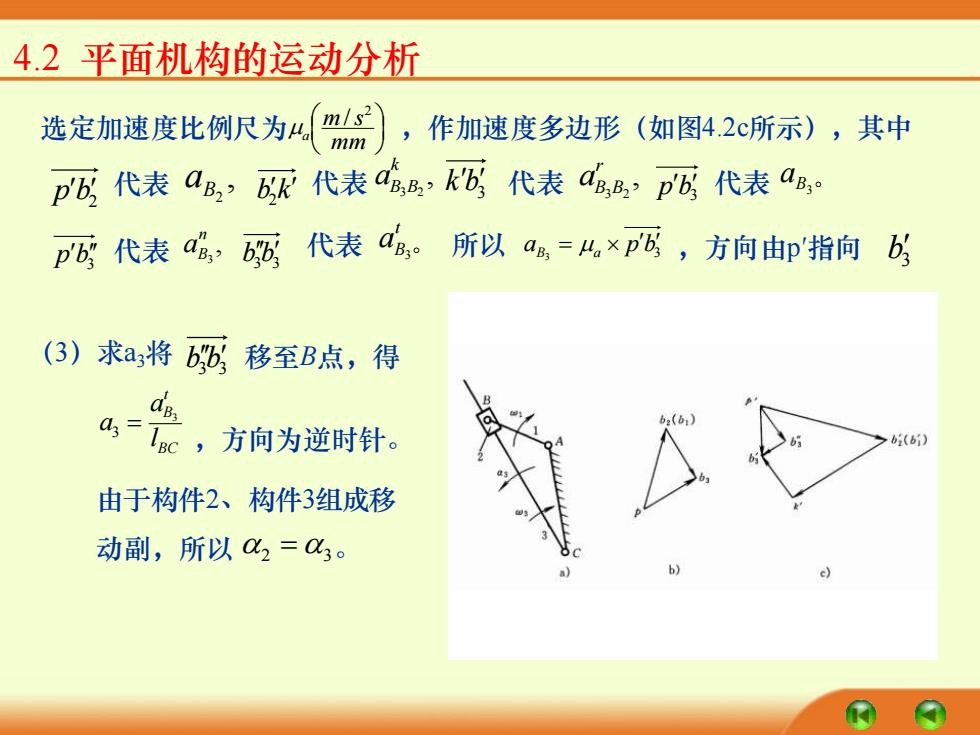
4.2平面机构的运动分析 选定加速度比例尺为(),作加速度多边形(如图42c所示),其中 pb代表aB,?6R代表4,k'b代表a,p'b代表a, p6代表,死代表a。所以a%=%×p6,方向p'指向b5 (3)求a将bb,移至B点,得 a=0,方向为逆时针。 6i() 由于构件2、构件3组成移 动副,所以C2=C3
4.2 平面机构的运动分析 选定加速度比例尺为 mm m s a 2 / ,作加速度多边形(如图4.2c所示),其中 p b2 代表 , B2 a bk 2 代表 , 3 2 k aB B 3 kb 代表 , 3 2 r aB B p b3 代表 B3 a p b3 代表 , 3 n aB 3 3 bb 代表 t B a 3 所以 aB3 a p b3 = ,方向由p′指向 3 b (3)求a3将 3 3 bb 移至B点,得 BC t B l a a 3 3 = ,方向为逆时针。 由于构件2、构件3组成移 动副,所以 2 = 3

4.3平面机构的力分析 平面机构力分析的主要目的:根据作用在平面机构上的已知外力和惯性力, 确定各运动副中的反力,进而确定为维持机构按给定规律运动所需的平衡 力或平衡力矩。 力分析通常用于计算机构各零件的强度、确定机械效率以及机械工作时 所需的驱动力矩等
4.3 平面机构的力分析 平面机构力分析的主要目的:根据作用在平面机构上的已知外力和惯性力, 确定各运动副中的反力,进而确定为维持机构按给定规律运动所需的平衡 力或平衡力矩。 力分析通常用于计算机构各零件的强度、确定机械效率以及机械工作时 所需的驱动力矩等
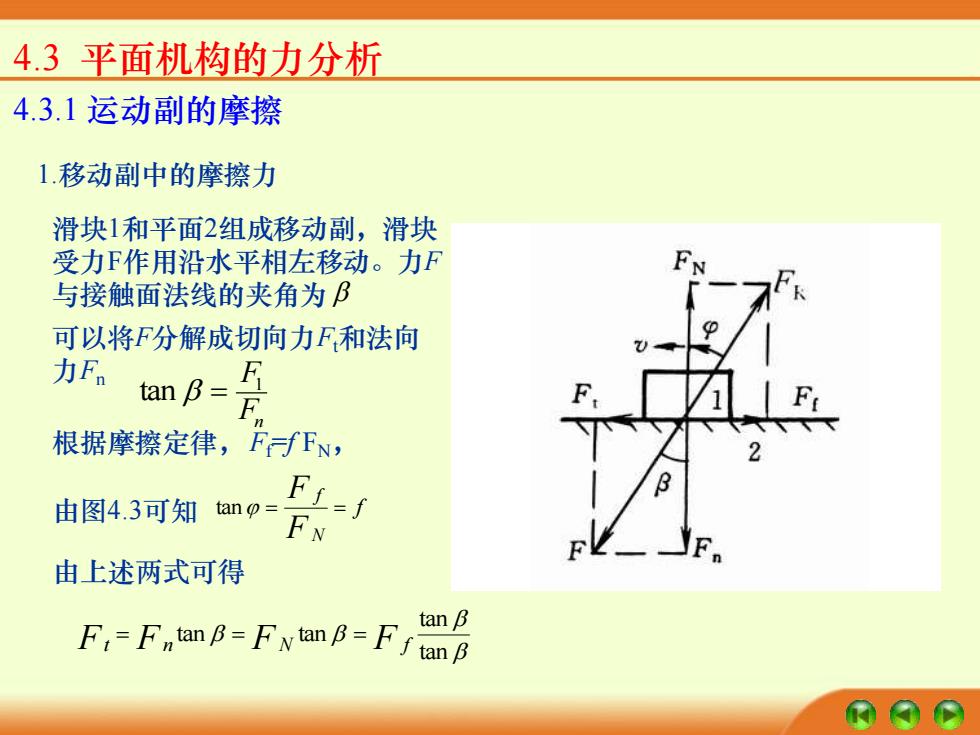
4.3平面机构的力分析 4.3.1运动副的摩擦 1.移动副中的摩擦力 滑块1和平面2组成移动副,滑块 受力F作用沿水平相左移动。力F 与接触面法线的夹角为阝 可以将F分解成切向力F和法向 力Fm amA月 根据摩擦定律,FfFN, 由图4.3可知anp= FL=f 由上述两式可得 tan B F=Fntan B-FytanB-F/tB
4.3 平面机构的力分析 4.3.1 运动副的摩擦 1.移动副中的摩擦力 滑块1和平面2组成移动副,滑块 受力F作用沿水平相左移动。力F 与接触面法线的夹角为 可以将F分解成切向力Ft和法向 力Fn Fn F1 tan = 根据摩擦定律,Ff=f FN, 由图4.3可知 f F F N f tan = = 由上述两式可得 tan tan Ft Fn tan F N tan F f = = =

4.3平面机构的力分析 由上式可知: (1)当B>p 外力F的作用线在摩擦角所包围的区域之外,此时 F>F,滑块作加速运动; (2)当B=p 外力F的作用线在摩擦角所包围的区域的面上,此 时F=F,滑块作等速运动。若滑块原来是静止的, 则保持静止不动; (3)当B<p 外力F的作用线在摩擦角所包围的区域的里面,此 时FF,滑块作减速运动,直到静止。若滑块原来 静不动,则不论用多大的外力都无法推动滑动使其 运动,这种现象称为自锁
4.3 平面机构的力分析 由上式可知: (1)当 外力F的作用线在摩擦角所包围的区域之外,此时 Ft>Ff,滑块作加速运动; (2)当 = 外力F的作用线在摩擦角所包围的区域的面上,此 时Ft=Ff,滑块作等速运动。若滑块原来是静止的, 则保持静止不动; (3)当 外力F的作用线在摩擦角所包围的区域的里面,此 时Ft<Ff,滑块作减速运动,直到静止。若滑块原来 静不动,则不论用多大的外力都无法推动滑动使其 运动,这种现象称为自锁