4.2平面机构的运动分析 构件1与构件2在B点组成转动副,所以Da,=DA,同理)c,=UC, 因此上式中只有两个未知数,可以用矢量多边形来求解。 ①如图所示,选定速度比例尺,(m/s/mm),任取极点p作矢量pb⊥AB, pb指向同o的转向一致,长度 pb=,这样矢量Db可以代表心。 M ②从b点作Us的方向线bc⊥BC 从p点作Uc的方向线pcL CD并交于c点 矢量pc代表Ue,矢量bc代表Um Ue=L•pc UcB=L,·bc
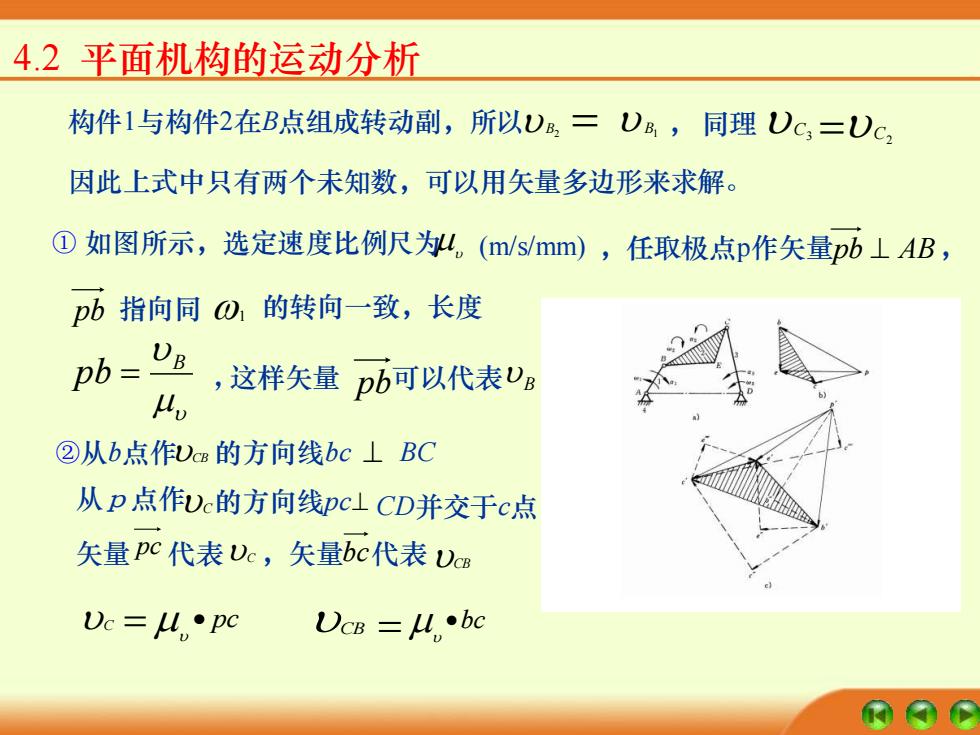
4.2 平面机构的运动分析 构件1与构件2在B点组成转动副,所以 B2 = B1 , 同理 C3 = C2 因此上式中只有两个未知数,可以用矢量多边形来求解。 ① 如图所示,选定速度比例尺为 (m/s/mm) ,任取极点p作矢量 pb ⊥ AB , pb 指向同 1 的转向一致,长度 B pb = 这样矢量 pb 可以代表 B ②从b点作 CB 的方向线bc ⊥ BC 从p点作 C 的方向线pc ⊥ 矢量 pc 代表 C ,矢量 bc 代表 CB C = • pc CB = •bc , CD并交于c点

4.2平面机构的运动分析 (3)求020由图4.1可知 02= UCB 将矢量b移到机构简图中的C点处,则可见O2为逆时针方向。 o-么 将矢量pc移到机构简图中的C点处,则可见O,为逆时针方向。 (4)求)E因为B、C、E为同一构件上的点,所以可得出下列方程式: UE=UB VEB Uc UEC 大小?OlB ? L·PC 方向? ⊥AB ⊥BE ⊥CD ⊥EC
4.2 平面机构的运动分析 (3)求 2 3 由图4.1可知 l BC CB = 2 将矢量 bc 移到机构简图中的C点处,则可见 2 为逆时针方向。 lCD C = 3 将矢量 pc 移到机构简图中的C点处,则可见 3 为逆时针方向。 (4)求 E 因为B、C、E为同一构件上的点,所以可得出下列方程式: E B = + EB = C + EC 大小 1l AB ? • PC ? ? 方向 ? ⊥ AB ⊥ BE ⊥CD ⊥ EC
4.2平面机构的运动分析 后一个方程只有两个未知数,可用图解法求解 如图4.1b所示,过b点作)EB 的方向线be⊥BE,过c点作 Uc的方向线ce⊥CE,两线交于e点 矢量pe代表D其大小为 Og=l,°pe ©a
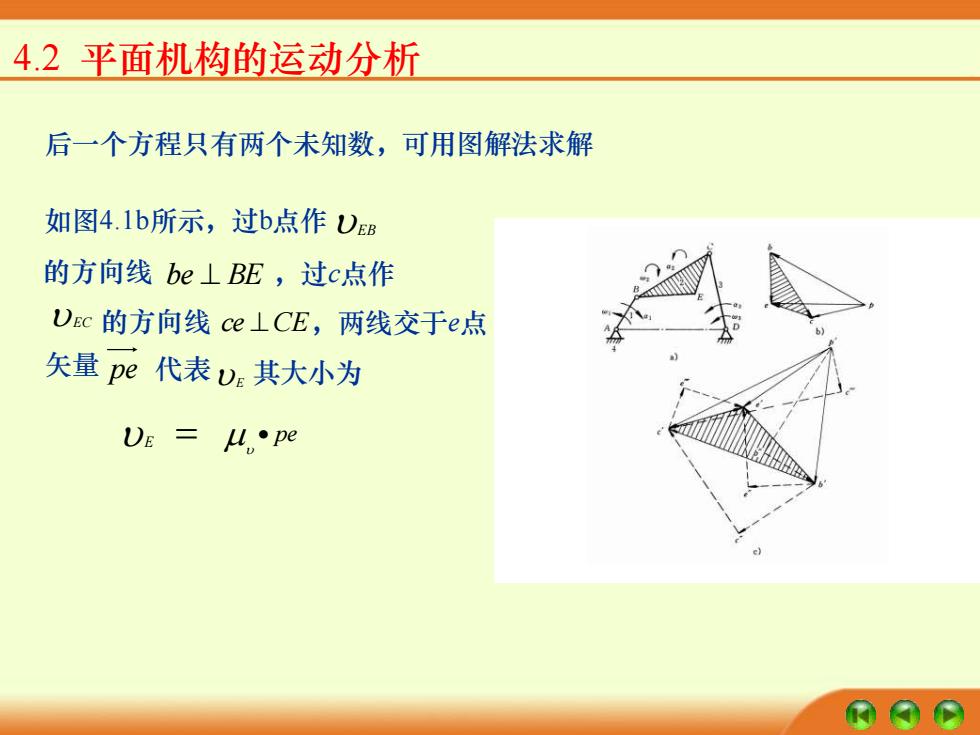
4.2 平面机构的运动分析 后一个方程只有两个未知数,可用图解法求解 如图4.1b所示,过b点作 EB 的方向线 be ⊥ BE ,过c点作 EC 的方向线 ce ⊥CE ,两线交于e点 矢量 pe 代表 E 其大小为 E = • pe

4.2平面机构的运动分析 2.加速度分析 (1)求CB由已知条件可知:0B=oLAB方向为B→ACB=01lB 方向垂直于AB,指向与01方向一致。 (2)求0c 根据相对运动原理,可建立如下方程式 dc +ac dn +as +dce +dc 大小 wileD ilxn alA8 Q2IB 方向C→D ⊥CDB→A⊥ABC→B⊥BC 式中有两个未知数,可用矢量图解法求解
4.2 平面机构的运动分析 2.加速度分析 n B n ( B = 1 l AB 1)求 B 由已知条件可知: = l AB 2 1 方向为B→ A 方向垂直于AB,指向与 1 方向一致。 式中有两个未知数,可用矢量图解法求解 (2)求 C 根据相对运动原理,可建立如下方程式 a n C a t C + = a n B a t B + a n CB + a t CB + 大小 lCD 2 3 ? l AB 2 1 1 l AB l AB 2 2 ? 方向 C→D ⊥ CD B→A ⊥ AB C→B ⊥ BC

4.2平面机构的运动分析 如图C所示,选定加速度比例尺4。(m/s2/m)任取一点P'为极点,作矢量 p6∥AB其大小为pb=2,指向为B-4,这样矢量p5可以代表 接着从b作矢量6万⊥AB,长度为b'b=,指向与a1方向一致,则矢量 b万代表a6;再作C∥BC,指向为C→B,长度为bc=,失量 b'c代表了aB作cc⊥BC 作为as的方向线;从p'作 pc”∥CD,方向为C→D,长度为 pc光,矢量pC代表 过c"作c"c⊥CD,作为 的方向线,与c"c'线相交于c
4.2 平面机构的运动分析 p b// AB ,其大小为 a n aB p b = ( / / ) 任取一点P′为极点,作矢量 2 如图C所示,选定加速度比例尺 a m s mm ,指向为B→A,这样矢量 p b 可以代表 接着从b″作矢量 bb ⊥ AB ,长度为 a t B a b b = ,指向与α1方向一致,则矢量 bb 代表 ;再作 b c // BC ,指向为C→B,长度为 a n CB a b c = ,矢量 b c t B a 代表了 n CB a c c ⊥ BC 作为 t aCB 的方向线;从p′作 作 p c //CD ,方向为C→D,长度为 a n a c p c = ,矢量 p c 代表 n C a 过 c 作 c c ⊥ CD ,作为 t C a 的方向线,与 c c 线相交于c′