
1-4求三角形窗函数(图1.22)的频谱,并作频谱图。 解:该三角形窗函数是一非周期函数,其时域数学描述如下: x(t) 1+2, ≤150 x(0)= 2 0≤1≤ -To/2 0 To/2 用傅里叶变换求频谱。 x(xed-Jr see d =0-20e*a+0+2h T a-200+20km T -7g-20eg。na-2 To ++2)ea-nema+2m 1 7p品r啡-el e-1-1tom l-cos 1 1 π2f2T ·2sm2 2 2-五snc2 2(y2 2 2
5 解:该三角形窗函数是一非周期函数,其时域数学描述如下: 用傅里叶变换求频谱。 -T0/2 0 T0/2 1 x(t) t − + − = 2 0 2 1 0 2 2 1 ( ) 0 0 0 0 T t t T t T t T x t − − − − = = / 2 / 2 2 2 0 0 ( ) ( ) ( ) T T j f t j f t X f x t e dt x t e dt 2 sin 2 ) 2 ( 2 sin 2 2 2sin 1 [1 cos ] 1 [ 1 1 ] 2 1 [ ] 2 1 2 2 ]} 2 ] [1 2 {[ 1 2 1 )]} 2 ) (1 2 [(1 )] 2 ) (1 2 {[(1 2 1 ) ] 2 ) (1 2 [ (1 2 1 ) 2 ) (1 2 (1 0 2 0 0 2 2 0 0 2 0 0 0 2 2 0 2 2 0 2 2 0 / 2 / 2 2 0 2 0 0 / 2 2 0 / 2 0 2 0 0 / 2 0 0 2 / 2 2 0 / 2 0 0 / 2 2 0 2 0 0 / 2 2 0 / 2 0 2 0 0 / 2 2 0 / 2 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 f T c T f T f T T f T f T f T f T e e f T e e j f T j f e dt T e dt j f T t T t e e d T t T t e e d j f T t de T t de j f T t e dt T t e dt T j f T j f T T j f t T j f t T j f t T j f t T j f t T j f t T j f t T j f t T j f t T j f t T j f t T j f t = = = − = = − − − + − − − = − + + − − = + + − + − − − − = − + + − = = − + + − − − − − − − − − − − − − − − − − − −
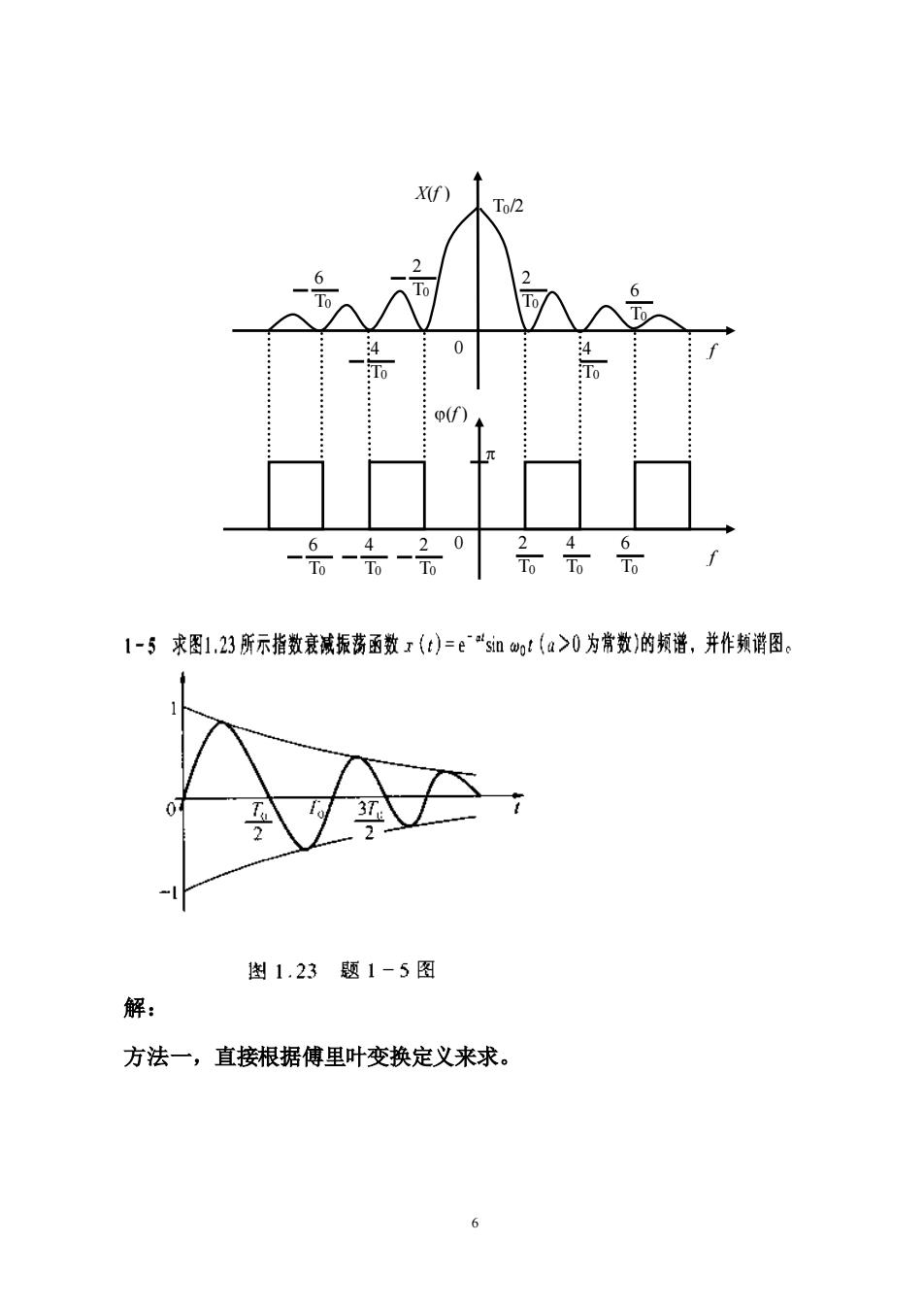
To/2 0 (f) 20 一一而一 而而而 f 1-5求图1.23所示指数衰减振荡函数r(t)=e“s如如t(a>0为常数)的频谱,并作频谱图。 37 2 出1.23题1-5图 解: 方法一,直接根据傅里叶变换定义来求。 6
6 解: 方法一,直接根据傅里叶变换定义来求。 X(f ) T0/2 0 2 T0 2 T0 f 6 T0 6 T0 (f ) 0 2 T0 4 T0 6 T0 2 T0 4 T0 6 T0 4 T0 4 T0 f

X(o)="x(t)e-dt e"sin wot edt =。mrew-eh -ey-eyd e-(atjo-j)t a+-)61 =[1 2'a+j(o+@o)a+j(o-@) 00 =a2+a2-02+2a0 方法二,根据傅里叶变换的频移特性来求。 单边指数衰减函数: 0t<0 f(t)= le-ar a>0,t≥0 其傅里叶变换为 F(@)=["f(t)e-dt =e-a.e-iedt =eae-a oo -(a+jo)0 1 (a+jo) a-jo =+0
7 方法二,根据傅里叶变换的频移特性来求。 单边指数衰减函数: 其傅里叶变换为 = − 0, 0 0 0 ( ) e a t t f t at 2 2 0 ( ) 1 ( ) 0 ( ) ( ) + − = + = − + = = = − − − − − − a a j a j a j e e e e dt F f t e dt at j t at j t j t a j a a j a j j a j j e a j j j e e e dt j e e dt j e e t e dt X x t e dt a j j t a j j t a j j t a j j t a j t j t j t a t j t j t 2 ] ( ) 1 ( ) 1 [ 2 ] ( ) ( ) [ 2 [ ) 2 ( ) 2 sin ( ) ( ) 2 2 0 2 0 0 0 0 0 ( ) 0 0 ( ) ( ) ( ) 0 ( ) 0 0 0 0 0 0 0 0 0 + − + = + − − + + = + − + − + + = = − = − = = − + − − + + − + + − + − − + − − − − −
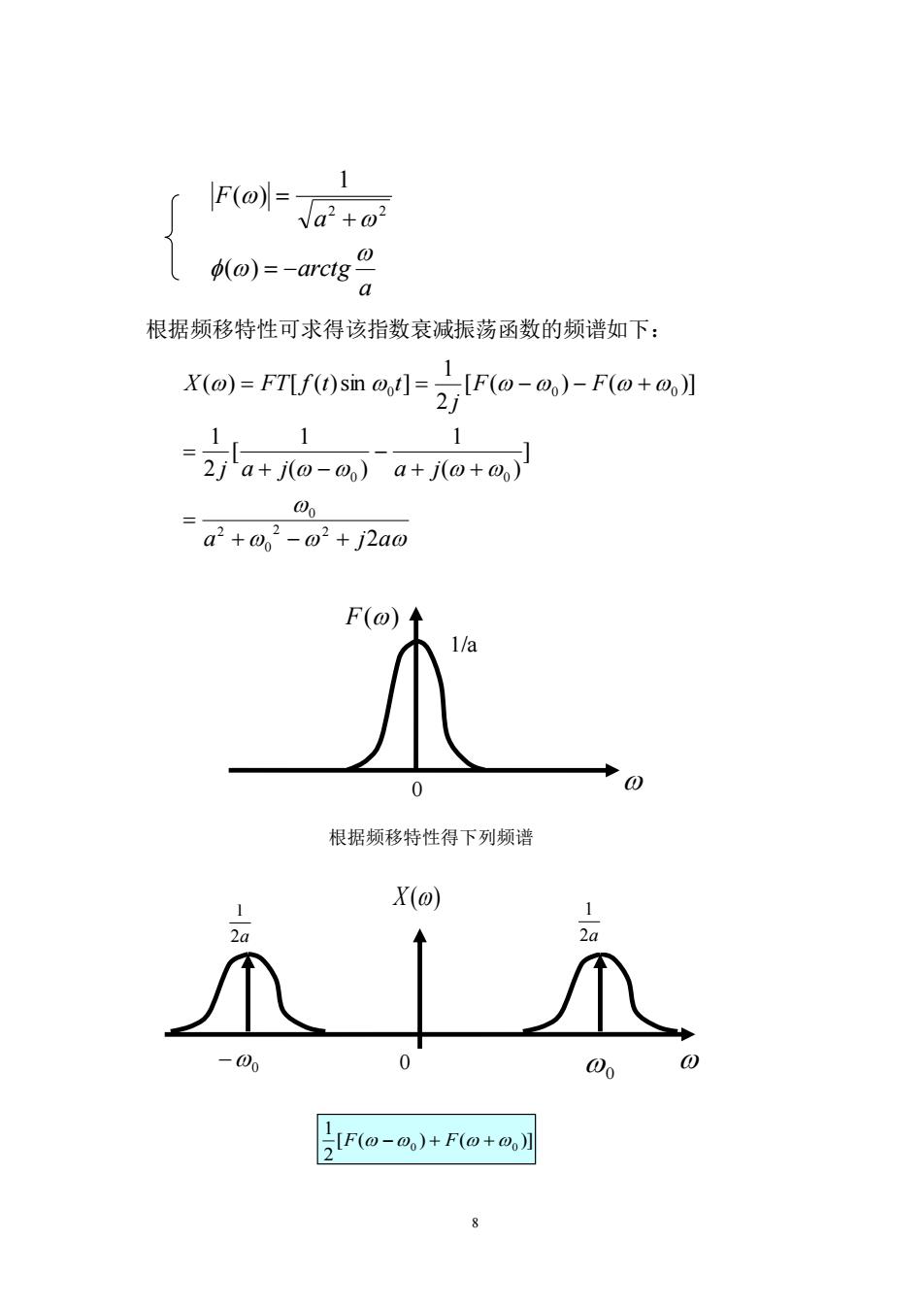
1 F(o)= va'+o Ke)-adg 根据频移特性可求得该指数衰减振荡函数的频谱如下: X(@)=FTIf(t)sin @ot]= Ra-a)-Fo+a】 1 1 1 2a+jo-,)a+j@+) 00 =a2+w2-02+j2a F(o)↑ 1/a 0 根据频移特性得下列频谱 X( Fo-eJ+Fro+a】
8 a arctg a F = − + = ( ) 1 ( ) 2 2 根据频移特性可求得该指数衰减振荡函数的频谱如下: 0 0 −0 F() 0 X () 1/a 2a 1 2a 1 根据频移特性得下列频谱 a j a j a j a j F F j X FT f t t 2 ] ( ) 1 ( ) 1 [ 2 1 [ ( ) ( )] 2 1 ( ) [ ( )sin ] 2 2 0 2 0 0 0 0 0 0 + − + = + + − + − = = = − − + [ ( ) ( )] 2 1 F −0 + F +0
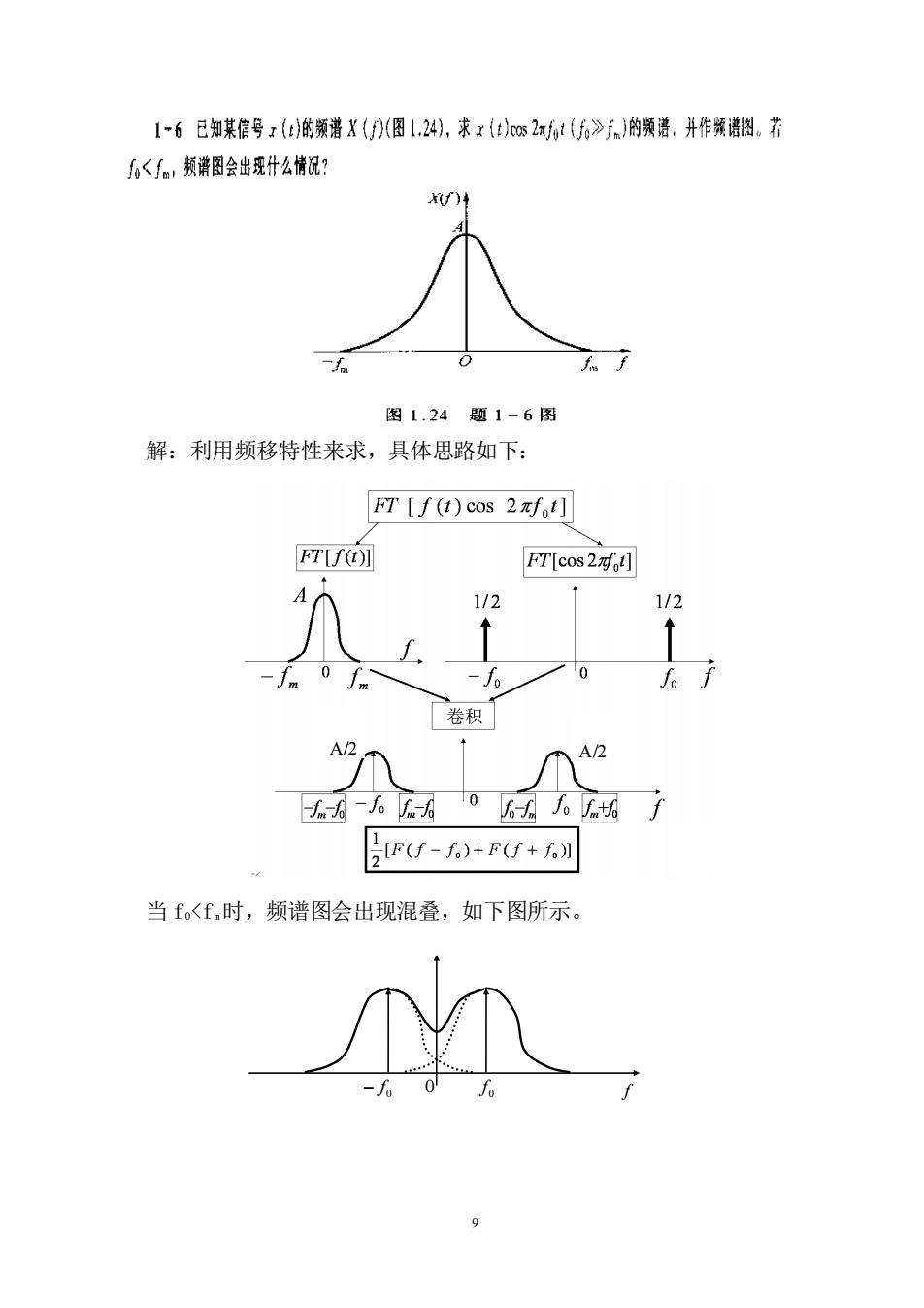
1-6已知某信号z(c)的颜谱X(U图L.24),求xt)s2xft(乐6》5,)的领谱.并作领谱。若 6<。,颊请图会出现什么情况? 图1.24题1-6图 解:利用频移特性来求,具体思路如下: FT[f(t)cos2πfo1] FTUSO] FT[cos2对] 1/2 1/2 「卷积 A/2 Ff-f+F+列 当f<f.时,频谱图会出现混叠,如下图所示
9 解:利用频移特性来求,具体思路如下: 当 f0<fm时,频谱图会出现混叠,如下图所示。 0 f 0 − f 0 f A/2 A/2