
注 此定理表明连续函数取变上限定积分再对 上限自变量x求导,其结果就等于被积 函数在上限自变量x处的函数值 若上限不是x而是x的函数心), 则求导时必须按复合函数的求导法则进行 d ax) (d=fa(x) 一般情况如果ft)连续,a(x)、b(x)可导, 则F)=feh的导数Fx)为 F-&fea=fioi-f树
一般情况 如 果 f (t)连续,a(x)、b(x)可导, 则F x f t dt b x a x = ( ) ( ) ( ) ( ) 的导数F(x)为 = ( ) ( ) ( ) ( ) b x a x f t dt dx d F x = f b(x)b(x) − f a(x)a(x) 注 此定理表明连续函数取变上限定积分再对 上限自变量 x 求导,其结果就等于被积 函数在上限自变量 x 处的函数值 若上限不是 x 而是 x 的函数 a(x), 则求导时必须按复合函数的求导法则进行 = ( ) [ ( ) ] [ ( )] ( ) a x a f t dt f a x a x dx d

证 F)=(a+e) -fy-fod, F'(x)=fb(x)]b'(x)-fa(x)】]a'(x) ["edt 例1求im cosx x-→0 k2 0 [分析]:这是。型不定式,应用洛必达法则 解 =-eox.(cosx)=sinx.e-cx
F x ( )f t dt a x b x ( ) ( ) 0 ( ) ( ) 0 = + f t dt b x = ( ) 0 ( ) ( ) , ( ) 0 f t dt a x − F(x) = f b(x)b(x) − f a(x)a(x) 例1 求 lim . 2 1 cos 0 2 x e dt x t x − → 0 0 [分析]:这是 型不定式,应用洛必达法则. 解 − 1 cos 2 x t e dt dx d , cos 1 2 − = − x t e dt dx d (cos ) 2 cos = − − e x x sin , 2 cos x x e − = 证

1 lim Sinx·ecos2x x-→0 -→0 2x 2e 例2设f(x)在(-oo,+oo)内连续,且f(x)>0. 证明函数F(x)= (t) 一在(0,+∞)内为单调增 心ft) 加函数. 证 云fo= 杰f0t=fx
2 1 cos 0 2 lim x e dt x t x − → x x e x x 2 sin lim 2 cos 0 − → = . 2 1 e = 例 2 设 f (x)在(−,+)内连续,且 f (x) 0. 证明函数 = x x f t dt tf t dt F x 0 0 ( ) ( ) ( ) 在(0,+)内为单调增 加函数. 证 x tf t dt dx d 0 ( ) = xf (x) x f t dt dx d 0 ( ) = f (x)
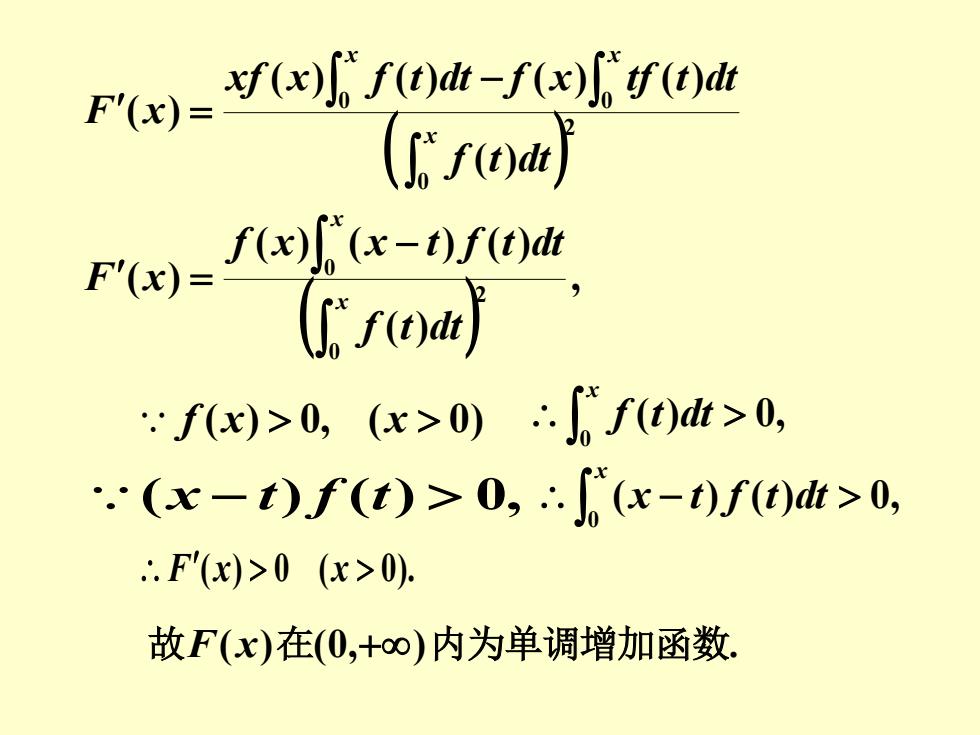
F'=wft-fx)fed (fe)j )Toofn roa 'f(x)>0,(x>0).f(t)dt>0, .(x-t)f(t)>0,.n(x-t)f(t)t>0, .F'(x)>0(x>0). 故F(x)在(0,+∞)内为单调增加函数
( ) , ( ) ( ) ( ) ( ) ( ) 2 0 0 − = x x f t dt f x x t f t dt F x f (x) 0, (x 0) ( ) 0, 0 x f t dt ( ) 2 0 0 0 ( ) ( ) ( ) ( ) ( ) ( ) − = x x x f t dt xf x f t dt f x tf t dt F x (x − t) f (t) 0, ( ) ( ) 0, 0 − x x t f t dt F(x) 0 (x 0). 故F(x)在(0,+)内为单调增加函数

例3设f(x)0,1上连续,且f(x)<1.证明 2x-f)=1在0,1上只有一个解 证令F(x)=2x-f)t-1, .·f(x)<1,∴.F'(x)=2-f(x)>0, F(x)在0,1上为单调增加函数 F(0)=-1<0, F()=1-f)dt=I1-f)lt>0 所以F(x)=0即原方程在0,1]上只有一个解
例 3 设 f (x)在[0,1]上连续,且f (x) 1.证明 2 ( ) 1 0 x − f t dt = x 在[0,1]上只有一个解. 证 令 ( ) 2 ( ) 1, 0 = − − F x x f t dt x f (x) 1, F(x) = 2 − f (x) 0, F(x)在[0,1]上为单调增加函数. F(0) = −1 0, = − 1 0 F(1) 1 f (t)dt = − 1 0 [1 f (t)]dt 所以F(x) = 0即原方程在[0,1]上只有一个解. 0