项点的度数(续) 设D=<V,E>为有向图,veV, v的出度(:v作为边的始点次数之和 v的入度(v小:v作为边的终点次数之和 v的度数(度)(吵:v作为边的端点次数之和 dy)='(y)+t(v) D的最大出度(D),最小出度8(D) 最大入度小(D),最小入度8(D) 最大度4(D),最小度&D) 例如(o)=4,t(a)=1,da)=5, 53=0,t(b)=3,db)=3, 6 D)=4,6(D)=0,(D=3, 8(D)=1,4(D=5,D)=3
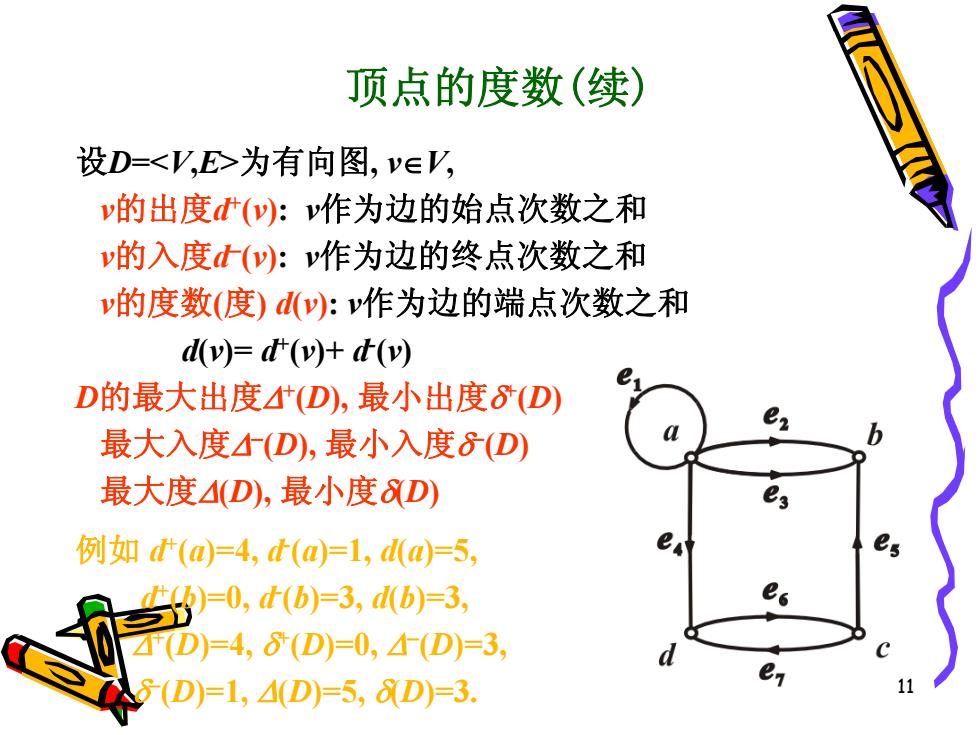
11 顶点的度数(续) 设D=<V,E>为有向图, vV, v的出度d + (v): v作为边的始点次数之和 v的入度d (v): v作为边的终点次数之和 v的度数(度) d(v): v作为边的端点次数之和 d(v)= d + (v)+ d - (v) D的最大出度+ (D), 最小出度 + (D) 最大入度 (D), 最小入度 (D) 最大度(D), 最小度(D) 例如 d + (a)=4, d - (a)=1, d(a)=5, d + (b)=0, d - (b)=3, d(b)=3, + (D)=4, + (D)=0, (D)=3, (D)=1, (D)=5, (D)=3
奇点与偶点: 度为奇数的点称为奇点度为偶数的点称为偶傲 d)=3,dy2)=1dy3)=4 dy4)=3,d(ys)=0,d(v6)=1, 2Y%为悬挂点:e2e为悬挂边, 为孤立点, 6 2y4为奇点,yy为偶点 ∑dy,)=12,G的边数m=-6 即∑d(y,)=2m 12
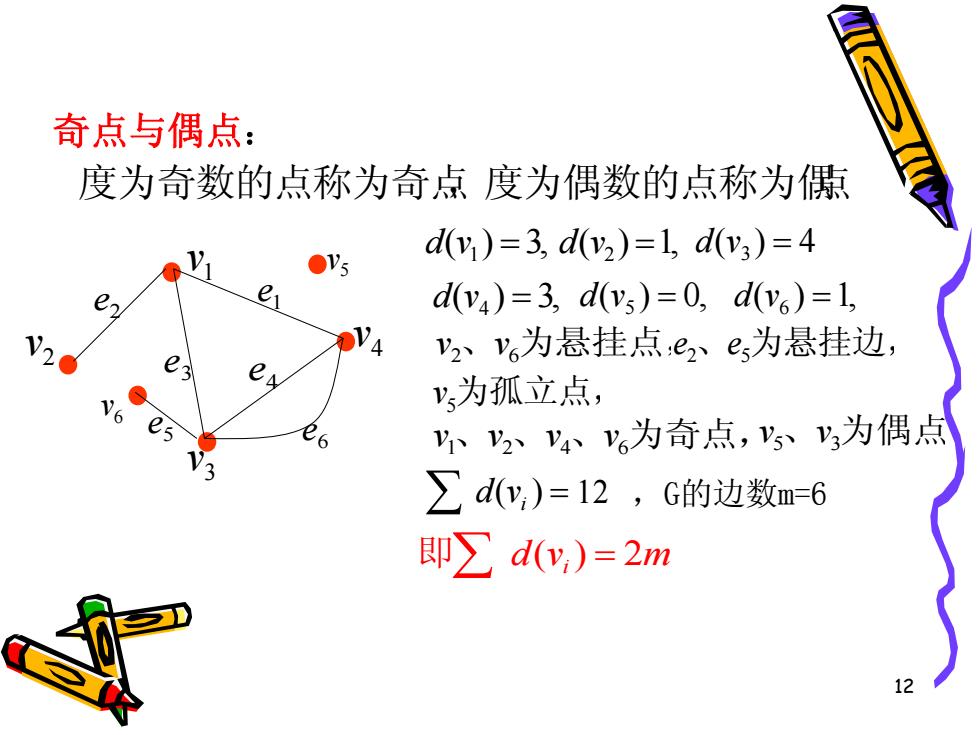
12 奇点与偶点: 度为奇数的点称为奇点,度为偶数的点称为偶点 1 v 2 v 3 v 4 v 2 e e3 e4 5 e 1 e 5 v v6 6 e ( ) 3, d v1 v2、v6为悬挂点,e2、e5为悬挂边, v5为孤立点,( ) 1, d(v3 ) 4 d v2 ( ) 3, d v4 ( ) 0, d v5 ( ) 1, d v6 v1、v2、v4、v6为奇点,v5、v3为偶点 d(vi ) 12 ,G的边数m=6 即 d(vi ) 2m

图论基本定理 握手定理 定理任意无向图和有向图的所有顶点度数之和都等 于边数的2倍即∑d(y)=2m,并且有向图的所有 顶点入度之和等于出度之和等于边数. 证G中每条边(包括环)均有两个端点,所以在计 算G中各顶点度数之和时,每条边均提供2度,m 条边共提供2度.有向图的每条边提供一个入度 一个出度,故所有顶点入度之和等于出度之和等 13
13 图论基本定理——握手定理 定理 任意无向图和有向图的所有顶点度数之和都等 于边数的2倍 , 并且有向图的所有 顶点入度之和等于出度之和等于边数. 证 G中每条边(包括环)均有两个端点,所以在计 算G中各顶点度数之和时,每条边均提供2度,m 条边共提供2m度. 有向图的每条边提供一个入度 和一个出度, 故所有顶点入度之和等于出度之和等 于边数. 即 d(vi ) 2m

握手定理(续) 推论在任何无向图和有向图中,奇度顶点的个数必 为偶数. 证设G=<V,E>为任意图,令 V={v|vEVAd()为奇数} V={v|vEVAd()为偶数} 则V1UV2=V,V∩V2=,由握手定理可知 2m=∑dy=∑d)+∑ EV 由舌2m∑()均为偶数,所以∑()也为偶数,但因为 顶点度数都为奇数,所以V必为偶数, 14
14 握手定理(续) 1 2 2 ( ) ( ) ( ) v V v V v V m d v d v d v 2 ( ) v V d v 1 ( ) v V d v 推论 在任何无向图和有向图中,奇度顶点的个数必 为偶数. 证 设G=<V,E>为任意图,令 V1 ={v | vVd(v)为奇数} V2 ={v | vVd(v)为偶数} 则V1∪V2 =V, V1∩V2 =,由握手定理可知 由于2m, 均为偶数,所以 也为偶数, 但因为 V1中顶点度数都为奇数,所以|V1 |必为偶数
图的度数列 设无向图G的顶点集={y1,2,yn} G的度数列:d(y),d(y2),d(yn) e3 如右图度数列:4,4,2,1,3 e es 设有向图D的顶点集={y1,V,Vn} D的度数列:d(y),dy2),d(yn) D的出度列:(y1),(2,(yn) D的入度列:t(y),t(y2,(ym) 如右图度数列:5,3,3,3 三出度列:4,0,2,1 入度列:1,3,1,2
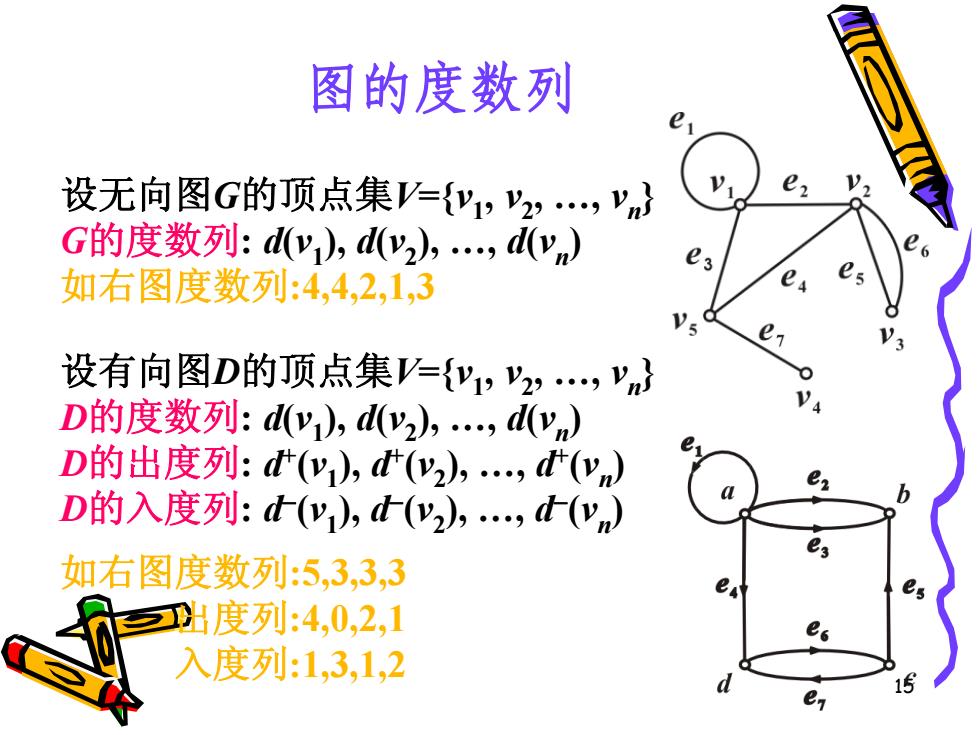
15 图的度数列 设无向图 G的顶点集 V={ v 1 , v 2 , . , v n } G的度数列 : d( v 1 ), d( v 2 ), . , d( v n ) 如右图度数列 : 4 , 4 , 2 , 1 , 3 设有向图 D的顶点集 V={ v 1 , v 2 , . , v n } D的度数列 : d( v 1 ), d( v 2 ), . , d( v n ) D的出度列 : d+ ( v 1 ), d+ ( v 2 ), . , d+ ( v n ) D的入度列 : d ( v 1 ), d ( v 2 ), . , d ( v n ) 如右图度数列 : 5 , 3 , 3 , 3 出度列 : 4 , 0 , 2 , 1 入度列 : 1 , 3 , 1 , 2