
离散数学试卷(二十一) 一、问答10% 已知定义在集合{a,b,c,d上的运算*如下表 h c d b 60 d d c a b 试问:1)<{a,b,c,d},*>是代数系统否?( 2)<{a,b,c,d,*>是子群否?( 3)<{a,b,c,d,*>是群否?( 4)<{a,b,c,d*>有单位元否?( ) 5)<{a,b,c,d,*>满足交换律香?( 二、填空10% 下表中的运算均定义在实数集上,请在相应的空格中打“√”或填上具体实数(不满足或无该项 者不填) + 结合律 交换律 么元(含 左、右 元) 零元(含 左、右零 元) 多
离散数学试卷(二十一) 137 一、问答 10% 已知定义在集合 {a,b, c, d} 上的运算*如下表: 试问:1) {a,b,c,d}, 是代数系统否?( ) 2) {a,b,c,d}, 是子群否?( ) 3) {a,b,c,d}, 是群否?( ) 4) {a,b,c,d}, 有单位元否?( ) 5) {a,b,c,d}, 满足交换律否?( ) 二、填空 10% 下表中的运算均定义在实数集上,请在相应的空格中打“√”或填上具体实数(不满足或无该项 者不填) + - × 结合律 交换律 幺元(含 左、右幺 元) 零元(含 左、右零 元) * a b c d a a b c d b b a d c c c d b a d d c a b
离散数学试卷(二十一) 三、有向图的矩阵表示应用15% VI V2 V3 V4 0010 己知某有向图的邻接矩阵如下:A= v20011 31101 试求:y3到y,的长度为4的有向 v41000 路径的条数。 四、图的同构15% 下面两图是否同构,若是给出点集间的同构映射。 v3 5 /g5 五、树的性质15% 已知某树有2个2度结点、3个3度结点、4个4度结点,问有几个叶子点(无其它度数点)。 六、最小生成树15% 使用普里姆算法求下图的最小生成树 6 5 加6 25 6 6 v3 七、自同构映射10% 令R={mm=a+bW2,a,b∈Q,+为普通加法},定义映射g:R→R为 g(a+bW2)=a-bW2,试证:g是<R,+>到<R,+>的自同构映射。 八、群与子群10% 设<G,*>是阶为6的群,证明它至多有一个阶为3的子群。 138
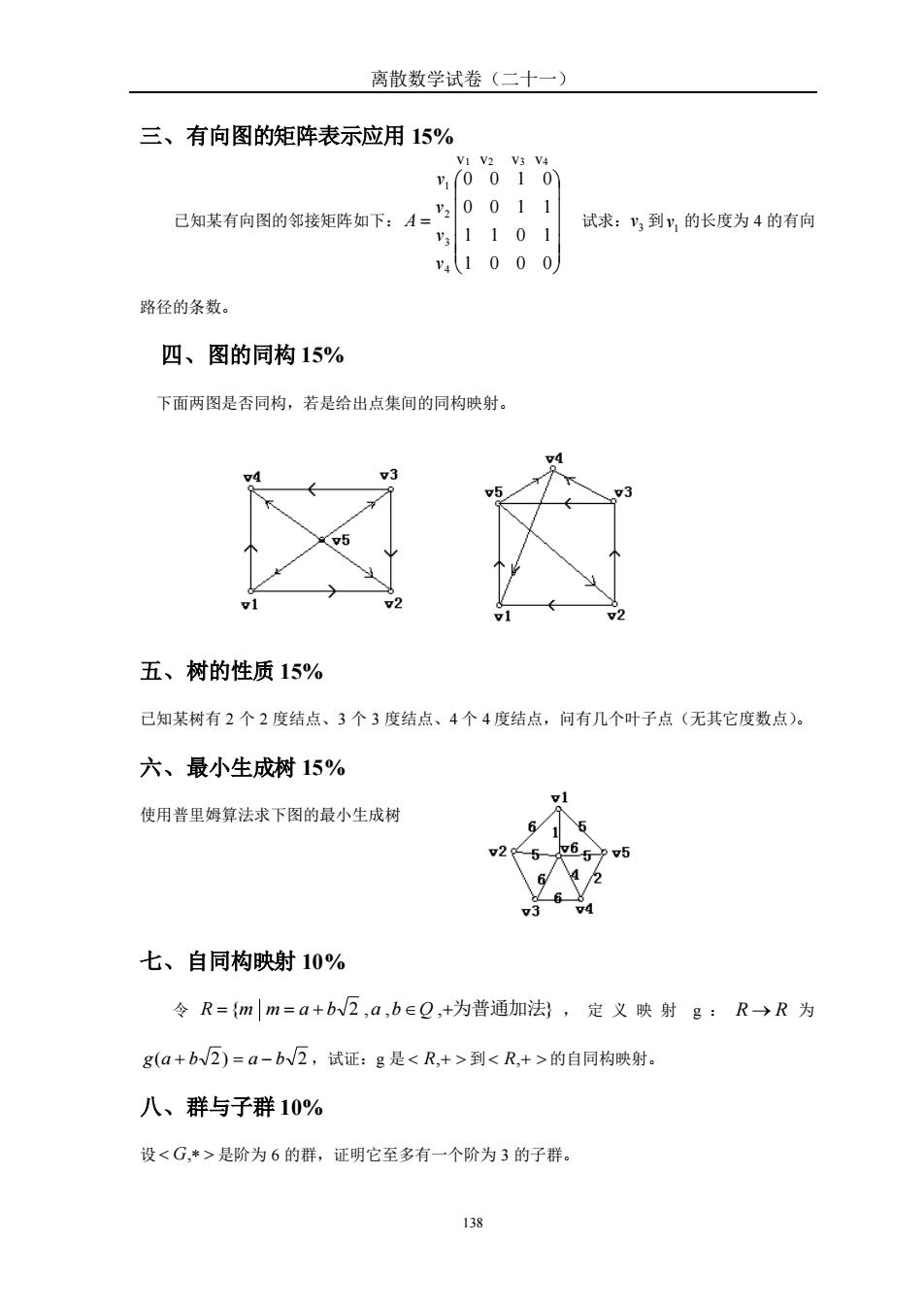
离散数学试卷(二十一) 138 三、有向图的矩阵表示应用 15% 已知某有向图的邻接矩阵如下: = 1 0 0 0 1 1 0 1 0 0 1 1 0 0 1 0 4 3 2 1 v v v v A 试求: 3 v 到 1 v 的长度为 4 的有向 路径的条数。 四、图的同构 15% 下面两图是否同构,若是给出点集间的同构映射。 五、树的性质 15% 已知某树有 2 个 2 度结点、3 个 3 度结点、4 个 4 度结点,问有几个叶子点(无其它度数点)。 六、最小生成树 15% 使用普里姆算法求下图的最小生成树 七、自同构映射 10% 令 R = {m m = a + b 2 ,a ,bQ ,+为普通加法} ,定义映射 g : R → R 为 g(a + b 2) = a − b 2 ,试证:g 是 R,+ 到 R,+ 的自同构映射。 八、群与子群 10% 设 G, 是阶为 6 的群,证明它至多有一个阶为 3 的子群。 v1 v2 v3 v4