
导航 2.直线的倾斜角是如何定义的?其范围如何? 提示:给定平面直角坐标系中的一条直线,如果这条直线与x 轴相交,将x轴绕着它们的交点按逆时针方向旋转到与直线重 合时所转的最小正角就是直线的倾斜角 直线与x轴平行或重合时,规定其倾斜角为0°.倾斜角的取值 范围是[0,)
导航 2.直线的倾斜角是如何定义的?其范围如何? 提示:给定平面直角坐标系中的一条直线,如果这条直线与x 轴相交,将x轴绕着它们的交点按逆时针方向旋转到与直线重 合时所转的最小正角就是直线的倾斜角. 直线与x轴平行或重合时,规定其倾斜角为0° .倾斜角的取值 范围是[0,π)

导 3.直线的斜率公式是什么?直线的倾斜角0与斜率k有何关系? 提示:ky2y,k=tan0. X2-X1 4.试写出倾斜角为0的直线的一个方向向量和一个法向量 提示:方向向量a=(cos0,sin0),法向量b=(sin0,cos0)
导航 3.直线的斜率公式是什么?直线的倾斜角θ与斜率k有何关系? 提示:k=𝒚𝟐-𝒚𝟏 𝒙𝟐-𝒙𝟏 ,k=tan θ. 4.试写出倾斜角为θ的直线l的一个方向向量和一个法向量. 提示:方向向量a=(cos θ,sin θ),法向量b=(-sin θ,cos θ)
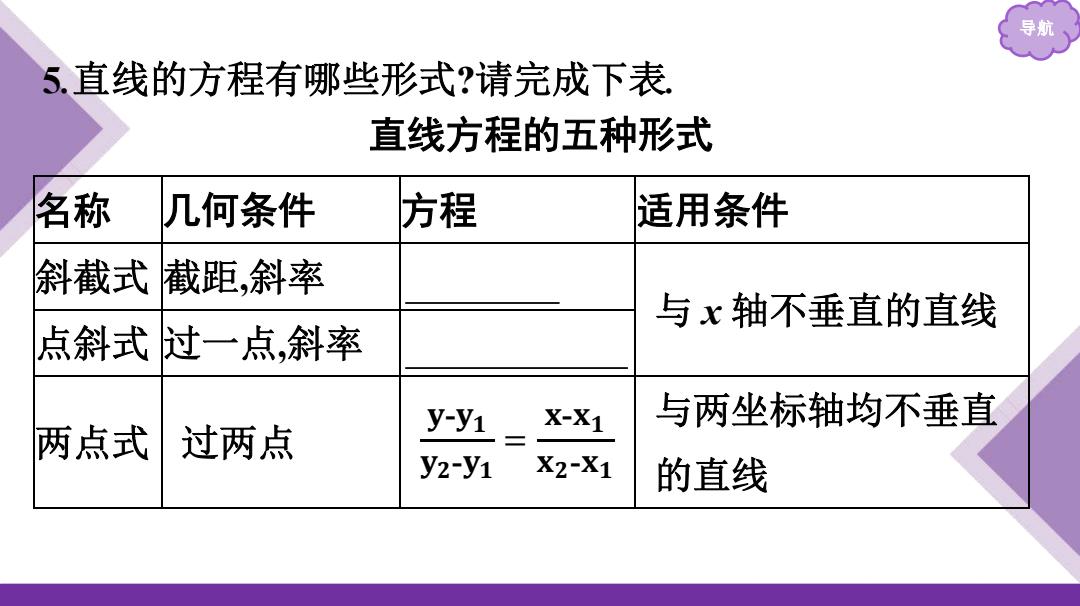
导航 5.直线的方程有哪些形式?请完成下表 直线方程的五种形式 名称 几何条件 方程 适用条件 斜截式 截距,斜率 与x轴不垂直的直线 点斜式过一点,斜率 X-X1 与两坐标轴均不垂直 两点式 过两点 y-y1 y2-y1 X2-X1 的直线
导航 5.直线的方程有哪些形式?请完成下表. 直线方程的五种形式 名称 几何条件 方程 适用条件 斜截式 截距,斜率 y=kx+b 与 x 轴不垂直的直线 点斜式 过一点,斜率 y-y0=k(x-x0) 两点式 过两点 𝐲-𝐲𝟏 𝐲𝟐-𝐲𝟏 = 𝐱-𝐱𝟏 𝐱𝟐-𝐱𝟏 与两坐标轴均不垂直 的直线

导航 名称 几何条件 方程 适用条件 在x轴、y 不过原点,且与两坐标 截距式 轴上的截距 + a 轴均不垂直的直线 Ax+By+C=0 般式 所有直线 (A2+B2+0)
导航 名称 几何条件 方程 适用条件 截距式 在 x 轴、y 轴上的截距 𝐱 𝐚 + 𝐲 𝐛 =1 不过原点,且与两坐标 轴均不垂直的直线 一般式 — Ax+By+C=0 (A2 +B2 ≠0) 所有直线

导 6.怎样判断两条直线平行或垂直? 提示:(1)两条直线平行 对于两条不重合的直线1,2,其斜率分别为k1,k2,则有 L1川2台k1=k2.特别地,当直线l1,2的斜率都不存在时,1与l2平行 (2)两条直线垂直 若两条直线1,2的斜率都存在,设为k1,k2,则11Ll2台k1k2=-1.当 一条直线的斜率为零,另一条直线的斜率不存在时,两条直线 垂直
导航 6.怎样判断两条直线平行或垂直? 提示:(1)两条直线平行 对于两条不重合的直线l1 ,l2 ,其斜率分别为k1 ,k2 ,则有 l1∥l2⇔k1=k2 .特别地,当直线l1 ,l2的斜率都不存在时,l1与l2平行. (2)两条直线垂直 若两条直线l1 ,l2的斜率都存在,设为k1 ,k2 ,则l1⊥l2⇔k1·k2 =-1.当 一条直线的斜率为零,另一条直线的斜率不存在时,两条直线 垂直