
关于条件概率,作如下几点说明: (1)P(B|A)可认为是A,B同时发生的次数占A发生次 数的比例.一般地,P(B|A)≠P(B),P(B|A)≠P(A), P(B|A)≠P(BA). (2)条件概率P(1A)也满足概率公理化定义中的三条, 即:①P(B|A)≥0;②P(2|A)=1;③若B,B2,.是可 数个两两互不相容的事件,则PUB)= ∑P(B,①.因而也是一个概率. 2024年8月27日星期二 7 目录○ 上页 下页 返回
2024年8月27日星期二 7 目录 上页 下页 返回 关于条件概率,作如下几点说明: (1) P B A ( | ) 可认为是 A B, 同时发生的次数占 A 发生次 数的比例.一般地, P B A P B ( | ) ( ) , P B A P A ( | ) ( ) , P B A P BA ( | ) ( ) . (2) 条件概率 P( | A) 也满足概率公理化定义中的三条, 即:① P B A ( | ) 0 ;② P A ( | ) 1 = ;③ 若 1 2 B B, , 是可 数 个 两两互不相容的事件,则 1 ( | ) i i P B A = = 1 ( | ) i i P B A = .因而也是一个概率.

关于条件概率,作如下几点说明: (3)计算条件概率可选择如下两种方法之一:①在原 样本空间2中,先计算P(AB),P(A),再按公式 P(B1A0=PCAB)计算:②由于事件A已经出现,它可以 P(4) 看成新的样本空间,因此可以在缩小后的样本空间A中 计算事件B发生的概率P(B|A). (4)一般地,P(B|A)≠P(AB). 2024年8月27日星期二 8 目录○ 上页 下页) 返回
2024年8月27日星期二 8 目录 上页 下页 返回 关于条件概率,作如下几点说明: (3) 计算条件概率可选择如下两种方法之一:① 在 原 样 本 空 间 中 , 先 计 算 P AB P A ( ), ( ) , 再 按 公 式 ( ) ( | ) ( ) P AB P B A P A = 计算;②由于事件 A 已经出现,它可以 看成新的样本空间,因此可以在缩小后的样本空间 A 中 计算事件 B 发生的概率 P B A ( | ) . (4) 一般地, P B A P A B ( | ) ( | ) .
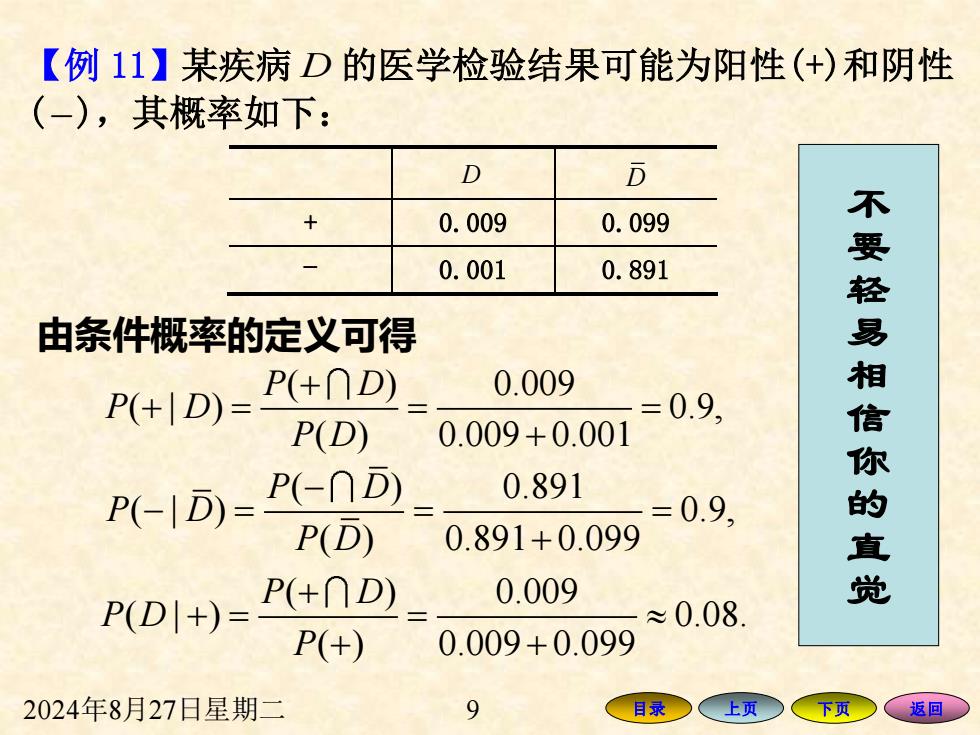
【例11】某疾病D的医学检验结果可能为阳性(+)和阴性 (-),其概率如下: D D 0.009 0.099 0.001 0.891 由条件概率的定义可得 P(+|D)= P(+∩D) 0.009 =0.9, P(D) 0.009+0.001 P(-|D)= P(-∩D) 0.891 =0.9, 不要轻易相信你的直党 P(D) 0.891+0.099 0.009 P(D|+)= P(+∩D) ≈0.08 P(+) 0.009+0.099 2024年8月27日星期二 9 目录○ 上页 下页 返回
2024 年 8 月27日星期二 9 目录 上页 下页 返回 【例 11 】某疾病 D 的医学检验结果可能为阳性(+)和阴性 ( −),其概率如下: D D + 0.009 0.099 − 0.001 0.891 由条件概率的定义可得 ( ) 0.009 ( | ) 0.9, ( ) 0.009 0.001 P D P D P D+ + = = = + ( ) 0.891 ( | ) 0.9, ( ) 0.891 0.099 P D P D P D− − = = = + ( ) 0.009 ( | ) 0.08. ( ) 0.009 0.099 P D P D P+ + = = + + 不要轻易相信你的直觉

【例12】设某种动物从出生起活20岁以上的概率为0.8, 活25岁以上的概率为0.5.求 (1)如果现在有一个20岁的这种动物,它能活25岁 以上的概率? (2)如果现在有一个20岁的这种动物,它活不到25 岁的概率? 解(1)设事件A={能活20岁以上};事件B={能活25岁 以上},则 P(B1A)=P(AB)0.5 =0.625 P(A4) 0.8 (2)P(B1A)=1-P(BA)=1-0.625=0.375 【注】该例说明P(B|A)=1-P(B|A). 2024年8月27日星期二 10 目录 上页 下页 返回
2024年8月27日星期二 10 目录 上页 下页 返回 【例 12】 设某种动物从出生起活 20 岁以上的概率为 0.8, 活 25 岁以上的概率为 0.5.求 (1) 如果现在有一个 20 岁的这种动物,它能活 25 岁 以上的概率? (2) 如果现在有一个 20 岁的这种动物,它活不到 25 岁的概率? 解 (1)设事件 A ={能活 20 岁以上};事件 B ={能活 25 岁 以上},则 ( ) 0.5 ( | ) 0.625. ( ) 0.8 P AB P B A P A = = = (2) P B A P B A ( | ) 1 ( | ) 1 0.625 0.375 = − = − = . 【注】该例说明 P B A P B A ( | ) 1 ( | ) = − .

二、乘法公式 由条件概率的定义容易推得概率的乘法公式(mulp lication formula): P(AB)=P(A)P(B A)=P(B)P(A B) 利用这个公式可以计算积事件的概率. 推广 P(A.An)=P(A)P(AA)P(AAA2).P(AnA.An1) 2024年8月27日星期二 11 目录○ 上页> 下页 返回
2024年8月27日星期二 11 目录 上页 下页 返回 二、 乘法公式 由条件概率的定义容易推得概率的乘法公式(multip lication formula): P AB P A P B A P B P A B ( ) ( ) ( ) ( ) ( ) = = 利用这个公式可以计算积事件的概率. 推广 1 1 2 1 3 1 2 1 1 ( ) ( ) ( ) ( ) ( ) P A A P A P A A P A A A P A A A n n n = −