语音量化的压缩扩张器 (sin)] 产生随 (sin]) ynl》 ygn》 绘制原始信号 机信号 和重建信号图 律压缩 b位量化 山律扩张 图9.2.1压缩器、AD变换器和扩张器的连接框图 压缩器的作用是把小信号放大,大信号缩小,所 以把压缩器后的信号进行量化,小信号的信噪 比就得到提高。而后通过扩张器,信号和量化 噪声同时作非线性变换,信号复原为原来电平, 小信号信噪比则保持较小的水平。 21
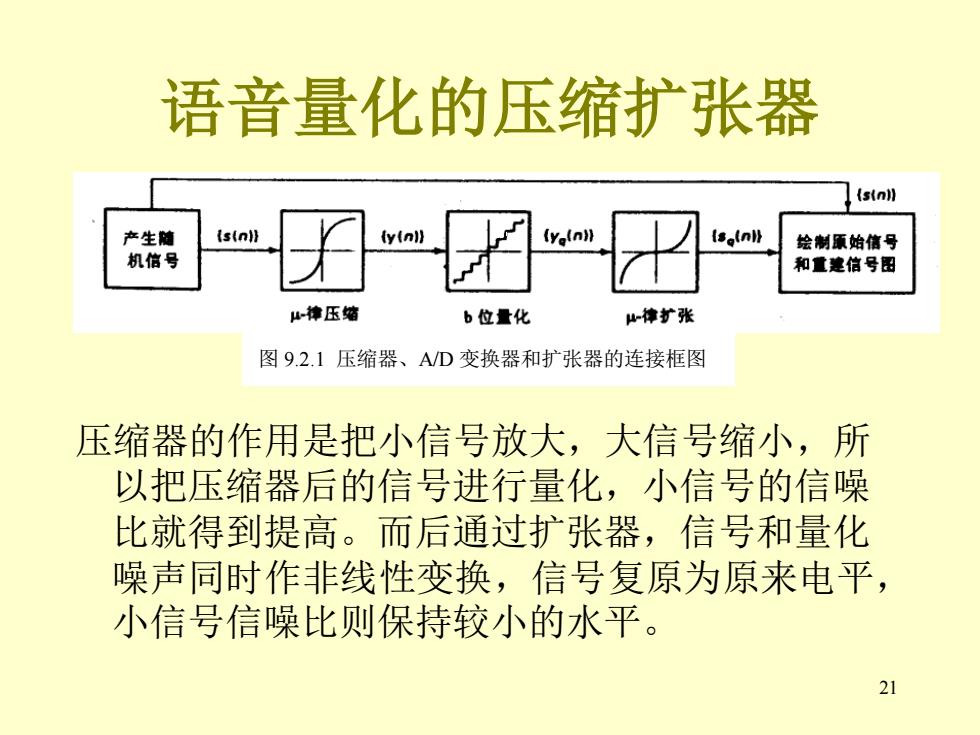
21 语音量化的压缩扩张器 压缩器的作用是把小信号放大,大信号缩小,所 以把压缩器后的信号进行量化,小信号的信噪 比就得到提高。而后通过扩张器,信号和量化 噪声同时作非线性变换,信号复原为原来电平, 小信号信噪比则保持较小的水平。 图 9.2.1 压缩器、A/D 变换器和扩张器的连接框图

语音量化的压缩扩张器 在我国的通信系统中使用的对数压缩器(称为u律 压缩器)具有如下输入输出幅度特性: VIn(1+ux/VD J= sign(x), x≤V,以≤V, ln(1+) 其中,x是归一化输入,y是归一化输出,sign() 是符号函数,μ=255,是控制压缩特性的参数。 由量化数字信号恢复模拟信号时,逆关系u律为: x='l+)M- -sign(y) 22
22 语音量化的压缩扩张器 在我国的通信系统中使用的对数压缩器(称为μ律 压缩器)具有如下输入输出幅度特性: 其中,x是归一化输入,y是归一化输出,sign(.) 是符号函数,μ=255,是控制压缩特性的参数。 由量化数字信号恢复模拟信号时,逆关系μ律为: ( ), , , ln(1 ) ln(1 | / |) sign x x V y V V x V y + + = ( ) (1 ) 1 | / | sign y V x y V + − =

语音量化的压缩扩张器 可以用MATLAB把压缩器和扩张器用函数程序 mulawcom和mulawexp:来表示,例如把压缩器 函数程序列写如下: function y=mulawcom(x,mu,V) if nargin<3V<max(abs(x)) V=max (abs (x)); end y=V/log(1+mu)*log(1+mu/V*abs (x)).*sign (x) 对u律扩张器和A-律的压扩器也可以按类似的方法 写出相应的子程序。 23
23 语音量化的压缩扩张器 可以用MATLAB把压缩器和扩张器用函数程序 mulawcom和mulawexp来表示,例如把压缩器 函数程序列写如下: function y= mulawcom(x,mu,V) if nargin<3 | V < max(abs(x)) V=max(abs(x)); end y=V/log(1+mu)*log(1+mu/V*abs(x)).*sign(x); 对μ律扩张器和A-律的压扩器也可以按类似的方法 写出相应的子程序

语音量化压缩器的特性 例9.2.1画出μ律和A律的压缩器输入输出曲线。 解:写出如下的MATLAB程序hc921 x=0:0.01:1; y=mulawcom (x,255,1); y1=A1 awcom(x,87.56,1); plot (x,y,x,y1,':';grid l on legend('\mu律','A律') 运行此程序的结果见图9.2.1。请注意二者非常相 似。 24
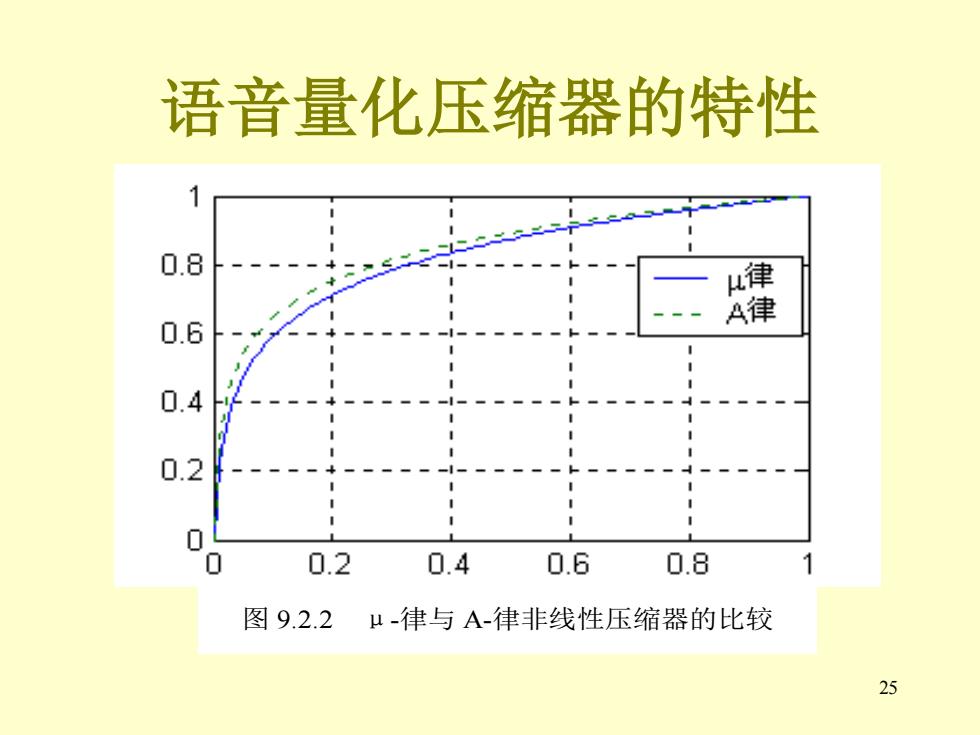
24 语音量化压缩器的特性 例9.2.1 画出μ律和A律的压缩器输入输出曲线。 解:写出如下的MATLAB程序hc921 x=0:0.01:1; y=mulawcom(x,255,1); y1=Alawcom(x,87.56,1); plot(x,y,x,y1,':');grid on legend('\mu律','A律') 运行此程序的结果见图9.2.1。请注意二者非常相 似
语音量化压缩器的特性 0.8 u律 A律 0.6 0.4 0.2 0 0.2 0.4 0.6 0.8 图9.2.2μ-律与A-律非线性压缩器的比较 25
25 语音量化压缩器的特性 图 9.2.2 μ-律与 A-律非线性压缩器的比较