
问题 上两个例子,一个是几何问题,求的 是以曲线y=x)为曲边,以[a,b]为底边的 曲边梯形的面积。一个是物理问题,求的是 速度函数为()的变速直线运动的物体在时 间区间[a,b]所走过的路程 归纳它们求的都是展布在某个区间上的总 量(总面积或总路程) 解决方法: 通过局部取近似(求微分),求和取极限 (微分的无限求和)的方法,把总量归结为 求一种特定和式的极限
问题 以上两个例子,一个是几何问题,求的 是以曲线 y = f(x)为曲边,以[a,b] 为底边的 曲边梯形的面积。一个是物理问题,求的是 速度函数为v(t)的变速直线运动的物体在时 间区间 [a,b] 所走过的路程 归纳它们求的都是展布在某个区间上的总 量(总面积或总路程) 解决方法: 通过局部取近似(求微分),求和取极限 (微分的无限求和)的方法,把总量归结为 求一种特定和式的极限

类似的例子还可以举出很多(几何、物 理的,在下一章定积分应用中即可见到) 这些问题虽然研究的对象不同,但解决 问题的思路及形式都有共同之处。为了一般 地解决这类问题,就有必要撇开它们的具体 含义,而加以概括、抽象得出定积分的概念
类似的例子还可以举出很多(几何、物 理的,在下一章定积分应用中即可见到) 这些问题虽然研究的对象不同,但解决 问题的思路及形式都有共同之处。为了一般 地解决这类问题,就有必要撇开它们的具体 含义,而加以概括、抽象得出定积分的概念

二、定积分的定义 定义设函数f(x)在4,b]上有界,在[4,b]中任意插入 若干个分点=X。<x<X2<.<X1<Xn=b 把区间可4,b]分成1个小区间,各小区间的长度依次为 △x:=;-x-1,(i=1,2,),,在各小区间上任取 一点5:(5:∈△r:),作乘积f(5:)△x,(i=1,2,.) 并作和S=∑f(5)△x;记入=max{△x1,△x2,.,△rn}, i=1 如果不论对,b1怎样的分法,也不论在小区间x:-1,x;上 点5:怎样的取法,只要当入→0时,和S总趋于 确定的极限I,我们称这个极限I为函数f(x)
定义 设函数 f (x)在[a,b]上有界,在[a,b]中任意插入 若干个分点 a x x x x x b = 0 1 2 n−1 n = 把区间[a,b]分成n 个小区间,各小区间的长度依次为 xi = xi − xi−1,(i = 1,2, ),在各小区间上任取 一点 i( i xi),作乘积 i xi f ( ) (i = 1,2, ) 并作和 i i n i S = f x = ( ) 1 ,记 max{ , , , } = x1 x2 xn , 如果不论对[a,b] 怎样的分法,也不论在小区间[ , ] xi−1 xi 上 点 i怎样的取法, 只要当 → 0时, 和S总趋于 确定的极限I ,我们称这个极限I 为函数 f (x) 二、定积分的定义
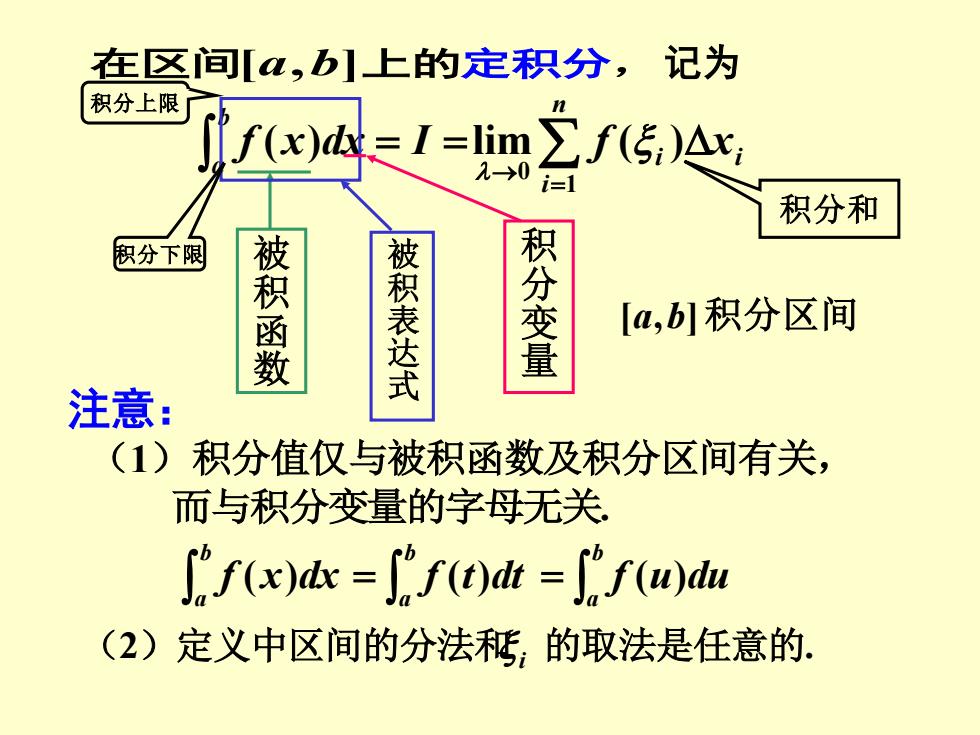
在区间[,b]上的定积分,记为 积分上限 ∫f(x)d∈I=lim∑f(传,)A, →0 i=1 积分和 积分下限 被积函 被积表达式 积分变量 [a,b]积分区间 注意: (1) 积分值仅与被积函数及积分区间有关, 而与积分变量的字母无关 f(x)d=∫f(t)adt=∫f(w)da (2)定义中区间的分法花,的取法是任意的
在区间[a,b]上的定积分, 记为 = = ba f (x)dx I i i ni f x = → lim ( ) 1 0 被积函数 被积表达式 积分变量 积分下限 积分上限 [a,b]积分区间 积分和 注意: (1) 积分值仅与被积函数及积分区间有关, 而与积分变量的字母无关. ba f (x)dx = ba f (t)dt = ba f (u)du (2)定义中区间的分法和 i 的取法是任意的

(3)当函数f(x)在区间[,b1上的定积分存在时 称f(x)在区间a,b上可积 三、存在定理 定理1 当函数f(x)在区间M,b]上连续时, 称f(x)在区间M,b]上可积 定理2 设函数f(x)在区间4,b]上有界, 且只有有限个间断点,则f(x)在 区间M,b]上可积
(3)当函数 f (x)在区间[a,b]上的定积分存在时, 称 f (x)在区间[a,b]上可积. 定理1 当函数 f (x)在区间[a,b]上连续时, 称 f (x)在区间[a,b]上可积. 定理2 设函数 f (x)在区间[a,b]上有界, 且只有有限个间断点,则 f (x)在 区间[a,b]上可积. 三、存在定理