内蒙古科技大学：《材料力学》课程PPT教学课件（机械类）第七章 应力状态分析 强度理论

s7—2 二向应力状态分析——解析法正负号规则：1yx正应力：拉为正；反之为负Txy切应力：使微元顺时针方向转动为正；反之为负。α角：由x轴正向逆时针转到斜截面外法线时为正；反之为负。0XTxyTyx-

11 x y  x  y  yx  xy a 使微元顺时针方向 转动为正；反之为负。 α角：由x 轴正向逆时针转 到斜截面外法线时为正；反 之为负。  y  a a   x y α n t  x yx  x §7—2 二向应力状态分析——解析法

S 7—2 二向应力状态分析——解析法2.正应力极值和方向确定正应力极值 +0,)+=(αx-0,)cos2α -tx, sin 2α-(o,OX22do=-(;-0,)sin2α-2ty cos2αda设α=α。时，上式值为零，即-(αx -,)sin 2αo -2tx cos2αo = 0(ax-a,)sin2 α。+txcos2 α = -2 t= 02即α=α。时，切应力为零

12     (  ) cos 2  sin 2 2 1 ( ) 2 1  x  y  x  y  xy 确定正应力极值         ( x y )sin 2 2 xy cos2 d d     设α＝α0 时，上式值为零，即  ( x  y )sin 20  2 xy cos20  0 2. 正应力极值和方向 sin2α τ cos2α 2τ 0 2 (σ σ ) 2 0 xy 0 α0 x y            即α＝α0 时，切应力为零 §7—2 二向应力状态分析——解析法

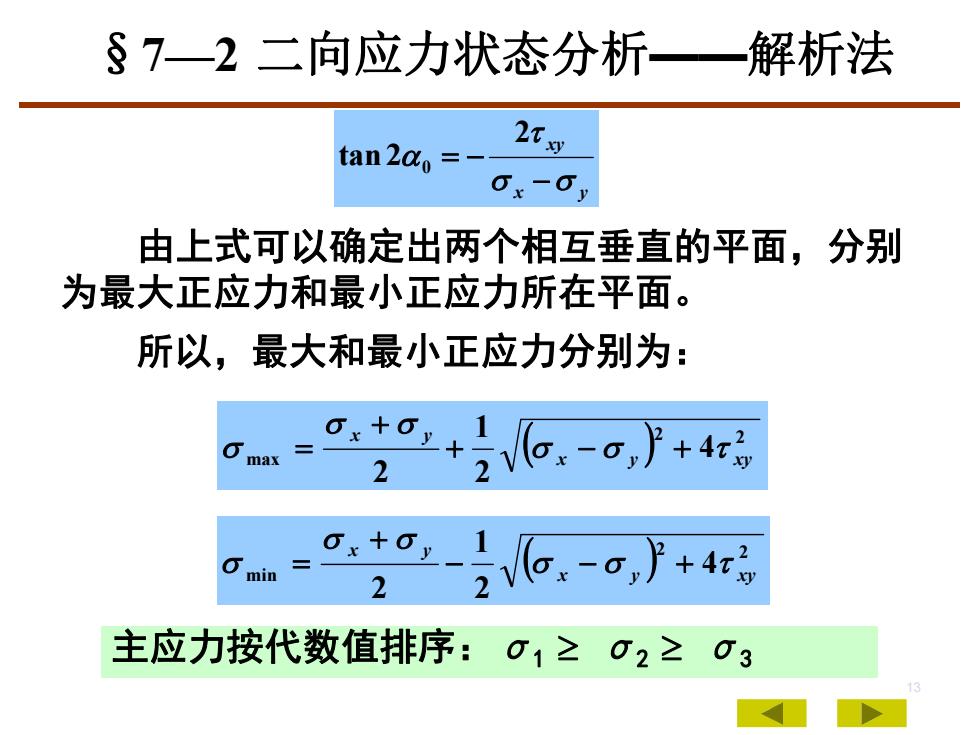
S7—2 二向应力状态分析——解析法2Txytan2α0ax-o,由上式可以确定出两个相互垂直的平面，分别为最大正应力和最小正应力所在平面。所以，最大和最小正应力分别为：ax+oy-0+4tOmax2a+ax-0+4tOmin2主应力按代数值排序：1≥2≥3

13 x y xy        2 tan 2 0 由上式可以确定出两个相互垂直的平面，分别 为最大正应力和最小正应力所在平面。 所以，最大和最小正应力分别为：   2 2 max 4 2 1 2 x y xy x y              2 2 min 4 2 1 2 x y xy x y            主应力按代数值排序：σ1  σ2  σ3 §7—2 二向应力状态分析——解析法

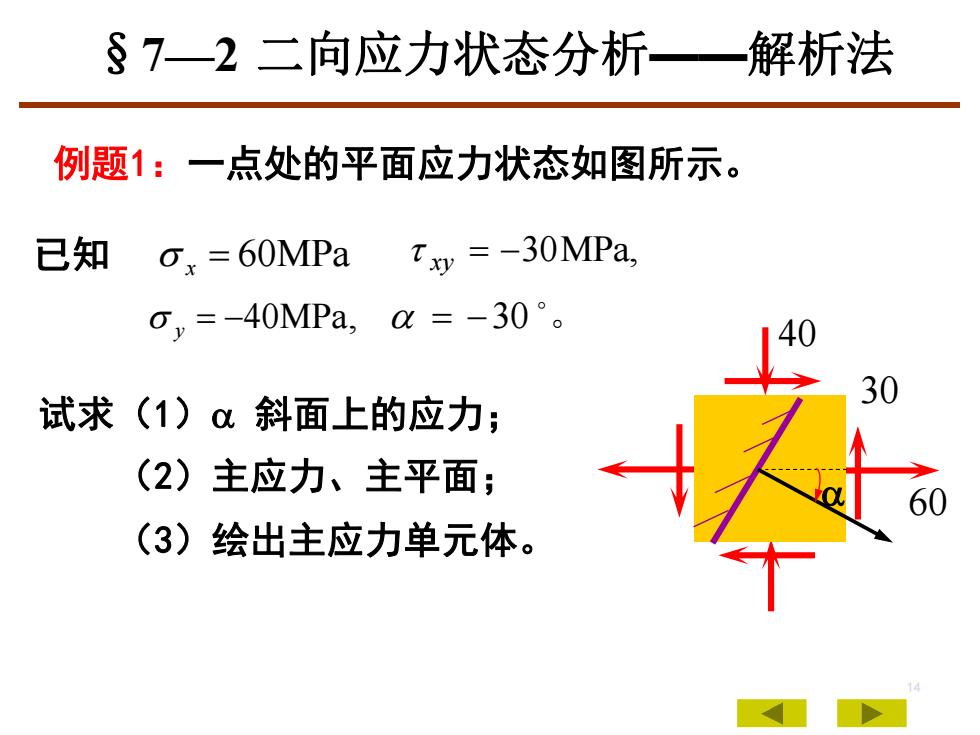
S 7—2 二向应力状态分析——解析法例题1：一点处的平面应力状态如图所示。已知T xy = -30MPa,αx = 60MPa,=-40MPa, α =-30°。4030试求（1）α斜面上的应力；（2）主应力、主平面；60（3）绘出主应力单元体

14 试求（1） 斜面上的应力； （2）主应力、主平面； （3）绘出主应力单元体。 例题1：一点处的平面应力状态如图所示。 40  60 30   30  。  60MPa  x  30MPa, xy   40MPa,  y 已知 §7—2 二向应力状态分析——解析法

S7—2 二向应力状态分析——解析法解：（1）α斜面上的应力Ox+o0x-0cos2α-Tr, sin2αOα22060-4060+40Txycos(-60°)+ 30sin(-60°)22= 9.02MPa?a.Osin 2α + tx, cos2αkd260 + 40sin(-60°)-30 cos(-60°)2= -58.3MPa

15 解：（1） 斜面上的应力          cos2 sin2 2 2 xy x y x y      cos( 60 ) 30sin( 60 ) 2 60 40 2 60 40           9.02MPa        sin 2 cos2 2 xy x y    sin( 60 ) 30cos( 60 ) 2 60 40         58.3MPa  y   x xy  §7—2 二向应力状态分析——解析法