第6章简单的超静定问题S6.1超静定问题及其解法静定结构:仅靠静力平衡方程就可以求出结构的约束反力或内力
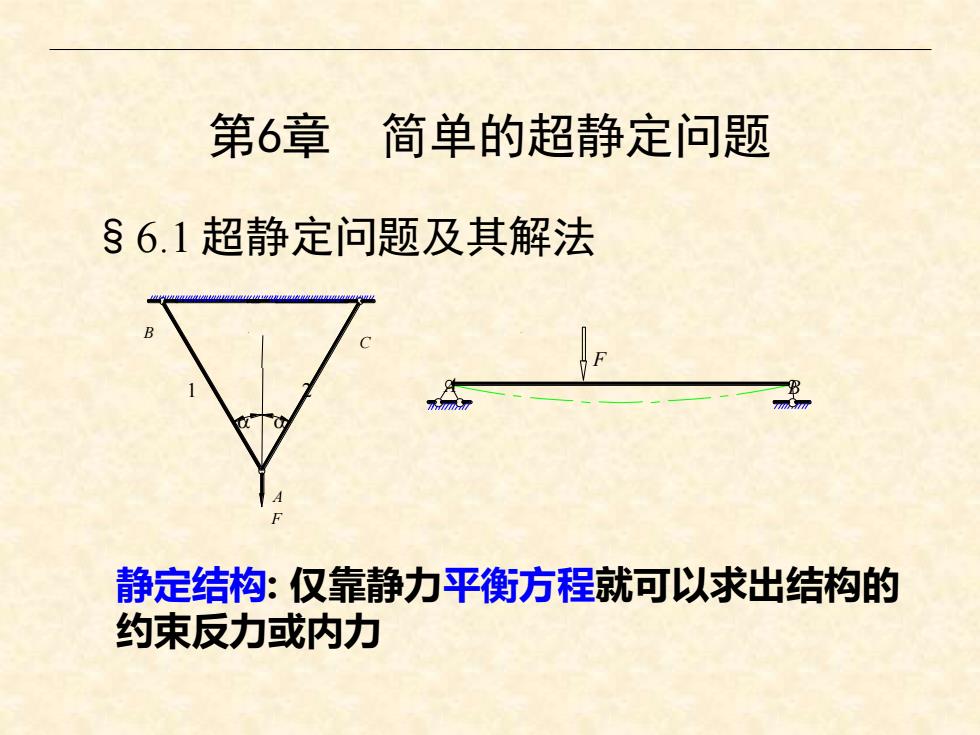
第6章 简单的超静定问题 §6.1 超静定问题及其解法 静定结构: 仅靠静力平衡方程就可以求出结构的 约束反力或内力 F 2 A B A F 1 B a a C
超静定结构(静不定结构):静力学平衡方程不能求解超静定结构的未知力的数目多于独立的平衡方程的数目;两者的差值称为超静定的次数
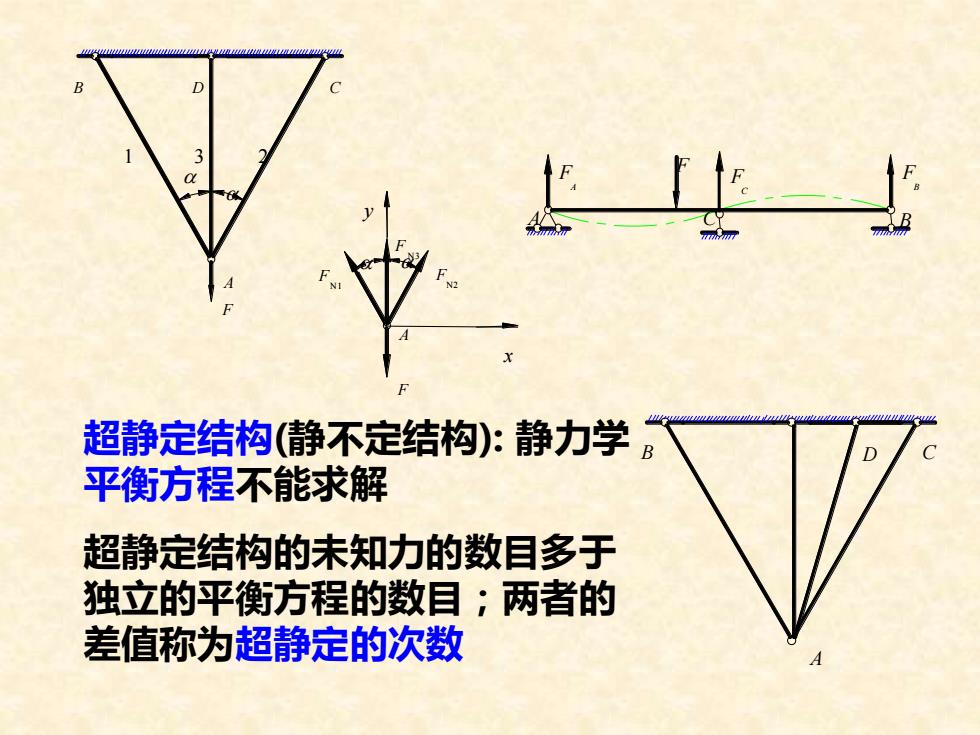
超静定结构(静不定结构): 静力学 平衡方程不能求解 超静定结构的未知力的数目多于 独立的平衡方程的数目;两者的 差值称为超静定的次数 B D C A 1 3 2 F a a F F C F B F A A C B A F a a F F F N2 N3 N1 y x B C A D

习惯上把维持物体平衡并非必需的约束称为多余约束,相应的约束反力称为多余未知力·超静定的次数就等于多余约束或多余未知力的数目。·从提高结构的强度和刚度的角度来说,多余约束往往是必需的,并不是多余的超静定的求解:根据静力学平衡条件确定结构的超静定次数,列出独立的平衡方程;然后根据几何物理关系得出需要的补充方程;则可求解超静定问题
•习惯上把维持物体平衡并非必需的约束称为多余约 束,相应的约束反力称为多余未知力。 • 超静定的次数就等于多余约束或多余未知力的数目。 •从提高结构的强度和刚度的角度来说,多余约束往 往是必需的,并不是多余的 •超静定的求解:根据静力学平衡条件确定结构的超 静定次数,列出独立的平衡方程;然后根据几何、 物理关系得出需要的补充方程;则可求解超静定问 题

补充方程:为求出超静定结构的全部未知力,除了利用平衡方程以外,还必须寻找补充方程,且使补充方程的数自等于多余未知力的数。·根据变形几何相容条件,建立变形几何相容方程结合物理关系(胡克定律),则可得出需要的补充方程。补充方程的获得,体现了超静定问题的求解技巧此处我们将以轴向拉压、扭转、弯曲的超静定问题进行说明
•补充方程:为求出超静定结构的全部未知力,除了 利用平衡方程以外,还必须寻找补充方程,且使补充 方程的数目等于多余未知力的数目。 •根据变形几何相容条件,建立变形几何相容方程, 结合物理关系(胡克定律),则可得出需要的补充方 程。 •补充方程的获得,体现了超静定问题的求解技巧。 此处我们将以轴向拉压、扭转、弯曲的超静定问题进 行说明

S 6.2 拉压超静定问题1拉压超静定问题解法例两端固定的等直杆AB,在C处承受轴向力F如图,杆的拉压刚度为EA,求杆的支反力解:一次超静定问题(1)力:由节点A的平衡条件列出杆轴线方向的平衡方程F+F-F=0
§6.2 拉压超静定问题 1 拉压超静定问题解法 例 两端固定的等直杆 AB,在 C 处承受轴向力F如 图,杆的拉压刚度为 EA,求杆的支反力. 解:一次超静定问题 FA + FB − F = 0 F B A F A B a b l F C (1)力:由节点 A 的平衡条件 列出杆轴线方向的平衡方程