
材料力学第十一章能量法

S11-1 概述1.能量法:利用功和能的概念及能量守恒定律,求解可变形固体的位移、变形和内力等的方法2.能量法的应用范围:(1)线弹性体:非线性弹性体(2)静定问题:超静定问题(3)是有限单元法的重要基础
§11-1 概 述 1.能量法: 利用功和能的概念及能量守恒定律,求解可变形 固体的位移、变形和内力等的方法。 2.能量法的应用范围: (1)线弹性体;非线性弹性体 (2)静定问题;超静定问题 (3)是有限单元法的重要基础

应变能·余能S11-21.应变能(1)线弹性体的各基本变形形式下的应变能表达式(参见上册)FNIV.=W-拉(压)杆2EAT?1圆轴扭转V.=W-2GIp梁弯曲V.=W-JM(a)dx2EI
§11-2 应变能•余能 1.应变能 (1) 线弹性体的各基本变形形式下的应变能表达式 (参见上册) 拉(压)杆 EA F l V W 2 2 = = N 圆轴扭转 G I T l V W p 2 2 = = 梁弯曲 l EI M x x V W 2 ( )d 2 = =
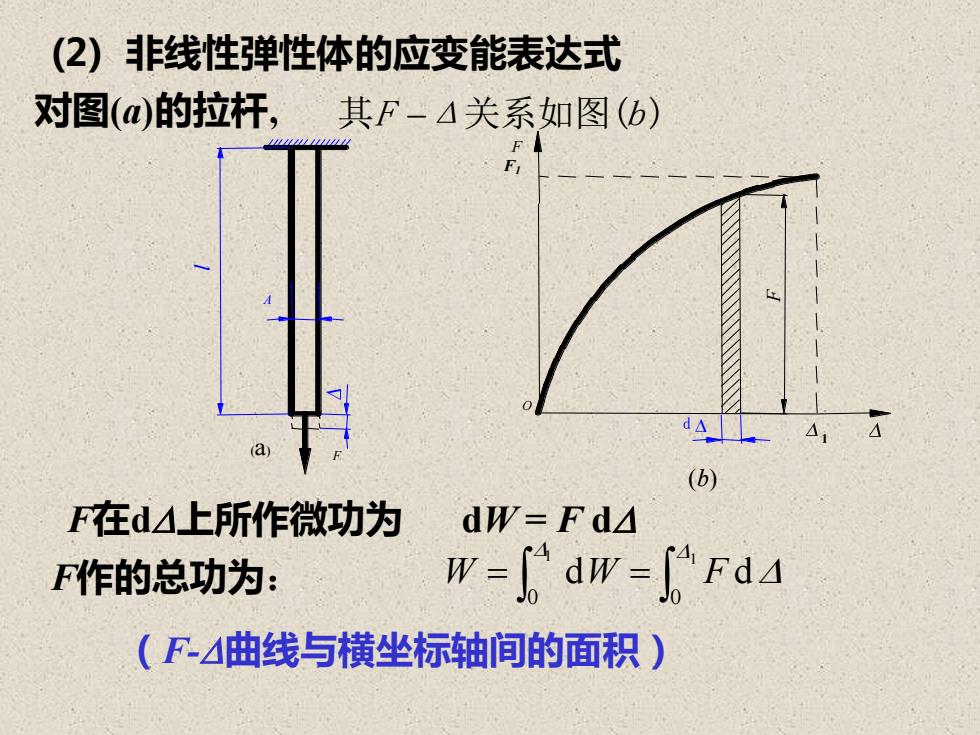
(2)非线性弹性体的应变能表达式对图(αa)的拉杆,其其F-4关系如图(b)FFiA(b)F在d△上所作微功为dW=F daW-dw-FdF作的总功为:(F-△曲线与横坐标轴间的面积)
(2) 非线性弹性体的应变能表达式 对图(a)的拉杆, 其F −Δ关系如图(b) F在d上所作微功为 dW = F d F作的总功为: = = 1 1 0 0 W dW F d (F-曲线与横坐标轴间的面积) A F l (a) F F1 F d O 1 (b)

由能量守恒得应变能:V.=W= ( Fd2(此为由外力功计算应变能的表达式)类似,可得其余变形下的应变能:梁受而弯曲:V.-Fdw梁受M.而弯曲:V-fM.de圆轴受M.而扭转:V-Mdo
由能量守恒得应变能: = = 1 0 d V W F (此为由外力功计算应变能的表达式) 类似,可得其余变形下的应变能: w 梁受F而弯曲: V = 0 F dw e 0 梁受M 而弯曲: V = Me d x 0 圆轴受M 而扭转: V = M x d