内蒙古科技大学：《材料力学》课程PPT教学课件（机械类）第七章 应力状态分析 强度理论

$71应力状态的概念20102TTZLZXZZaJL10单元体上没有切应力的面称为主平面；主平面上的正应力称为主应力，分别用1,02,03表示，并且01≥02≥03该单元体称为主单元体

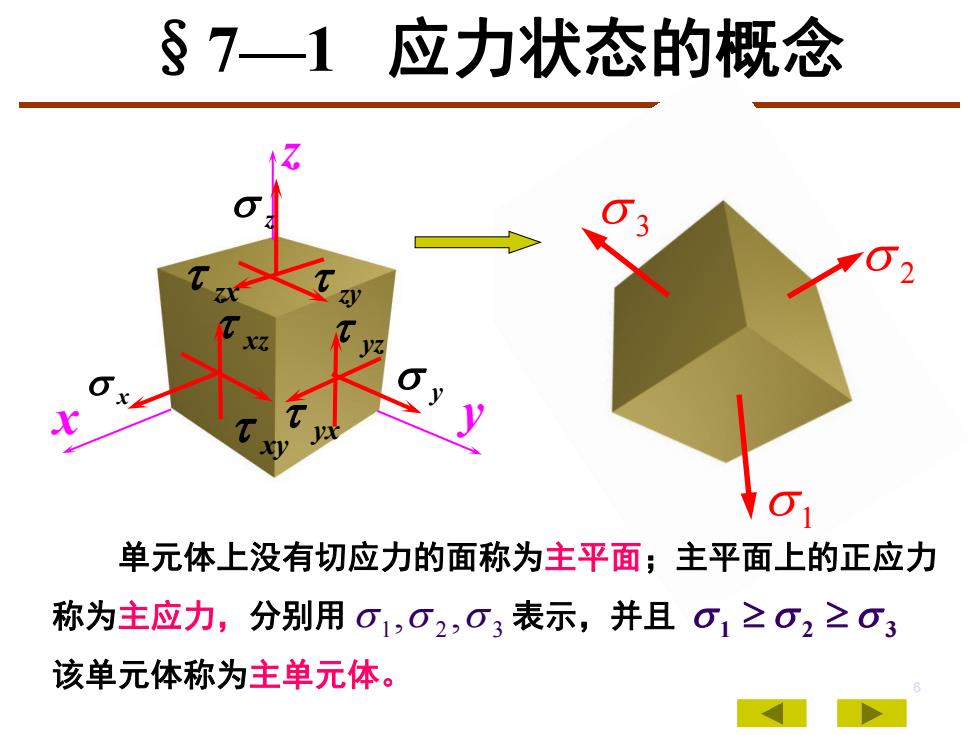
6  1  2  3 x y z  x  y  z  xy  yx  yz  zy  zx  xz 单元体上没有切应力的面称为主平面；主平面上的正应力 称为主应力，分别用 表示，并且 该单元体称为主单元体。 1 2 3  , ,  1   2   3 §7—1 应力状态的概念

s71应力状态的概念空间 (三向)应力状态：三个主应力均不为零平面（二向)应力状态：一个主应力为零单向应力状态：两个主应力为零DO101

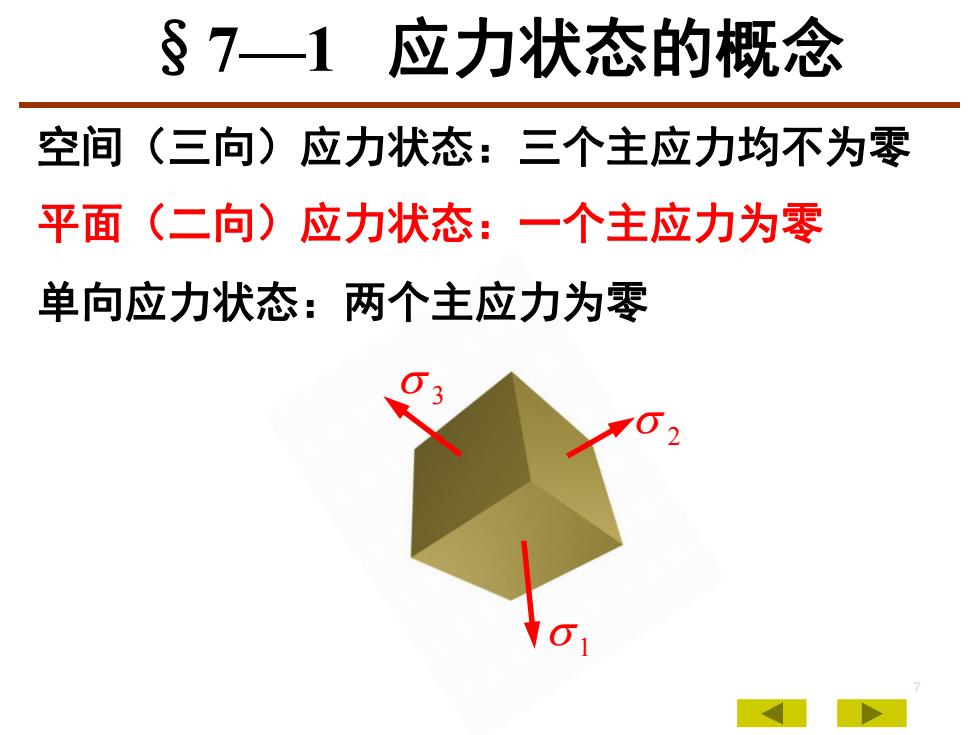
7  1  2  3 空间（三向）应力状态：三个主应力均不为零 平面（二向）应力状态：一个主应力为零 单向应力状态：两个主应力为零 §7—1 应力状态的概念

s 7—2 二向应力状态分析——解析法1.斜截面上的应力nT.q20yx0dTxyTxdAO2Xyxt0yZF,=0F,=0E

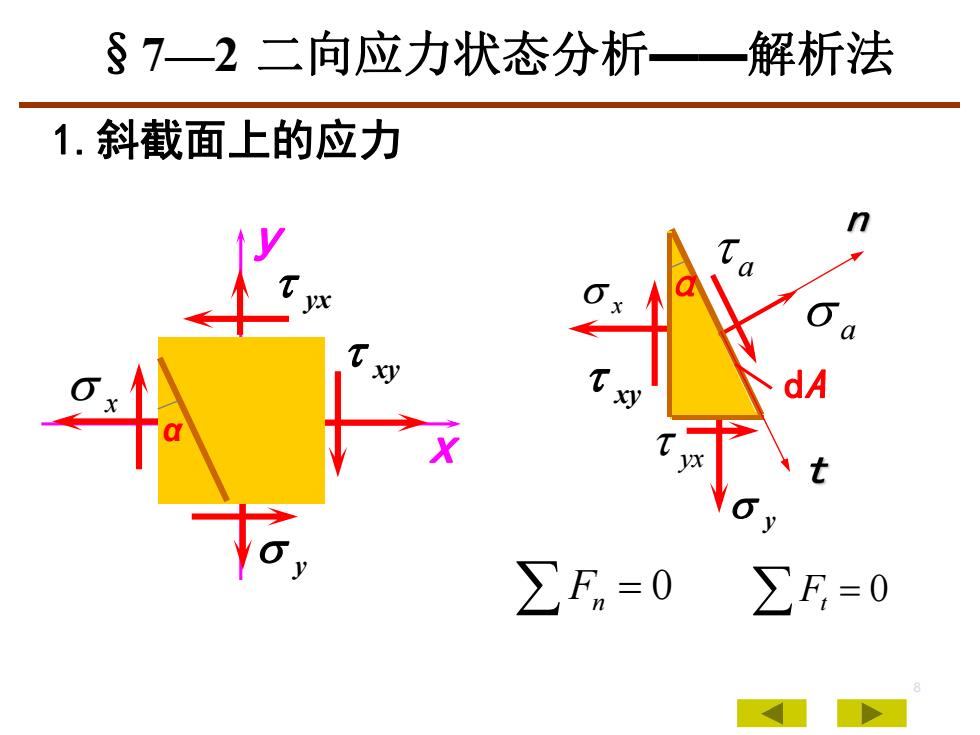
8 x y  x  y  yx  xy α   0 Fn   0 Ft 1.斜截面上的应力  y  a a   xy dA  x α yx  §7—2 二向应力状态分析——解析法

s7—2 二向应力状态分析—一解析法nKo列平衡方程OaX9aZF,=0TxydAT.&dA+tx(dAcosα)sinα-o,(dAcosα)cosα +yxtOT(dAsinα)cosα-,(dAsinα)sinα = 0ZF=0tadA-tx,(dAcosα)cosα-o,(dAcosα)sinα+Tyx(dAsinα)sinα+o,(dAsinα)cosα = 0

9 Fn  0 ( sin ) cos ( sin )sin 0 ( cos )sin ( cos ) cos                    dA dA dA dA dA yx y xy x Ft  0 ( sin )sin ( sin ) cos 0 ( cos ) cos ( cos )sin                    dA dA dA dA dA yx y xy x  y  a a   xy dA  x α yx  §7—2 二向应力状态分析——解析法

s7—2 二向应力状态分析——解析法cos α ==(1+ cos 2α)2利用三角函数公式sin’ α ==(1-cos 2α)22sinα cosα = sin 2α并注意到 x=x,化简得Gα=(0, +0,)+(o,-0,)cos 2α-T y sin 2α=(αx-0,)sin 2α+tx cos2α

10 利用三角函数公式 (1 cos 2 ) 2 1 cos 2    (1 cos 2 ) 2 1 sin 2    2sin cos  sin2 { 并注意到  yx   xy 化简得     (  ) cos 2  sin 2 2 1 ( ) 2 1  x  y  x  y  xy   (  )sin 2  cos 2 2 1  x  y  xy §7—2 二向应力状态分析——解析法