
第五章例:一长直金属槽的长度方向平行于z轴,其横截面如图所示,其侧壁与底面电位均为0,而顶盖电位UaU(x)=U。d(x,b) =U(x). 1.d(x)=0元2.U(x)=U, sin XOC求槽内电位Φ的解。解:由题意,Φ沿z方向是没有变化的,而槽的边界是与直角坐标系的坐标面平行的。1、选直角坐标系:如图所示。13.a2、拉氏方程:(5-2-1 2)COx?Oy112025/6/11电磁场理论
电磁场理论 2025/6/11 第五章 11 例:一长直金属槽的长度方向平行于z轴,其横截面 如图所示,其侧壁与底面电位均为0,而顶盖电位 (x,b) =U(x). 1. 2. ( ) , U0 U x = ( ) sin x, a U x Um = 求槽内电位 的解。 (x) = 0 解:由题意, 沿z方向是没有变化的,而槽的 边界是与直角坐标系的坐标面平行的。 1、选直角坐标系:如图所示。 2、拉氏方程: 0 2 2 2 2 = + x y (5-2-12) 13

第五章3、边界条件:Uw条件边界d(x)=0Φ=0 >x=0,0≤y≤b(5-2-13Φ=0x=a,0≤y≤b(5-2-14)=O>=0,0≤x≤a15.(5-2-15)Φ=U(x) >y=b, 0≤x≤α (5-2-1 6)4、用分离变量法分离出两个常微分方程:d(x, y) = f(x)·g(y)令(5-2-1 7)122025/6/11电磁场理论
电磁场理论 2025/6/11 第五章 12 3、边界条件: 条件 边界 (x) = 0 = 0 x = 0, 0 y b (5-2-13) = 0 x = a, 0 y b (5-2-14) = 0 y = 0, 0 x a (5-2-15) =U(x) y = b, 0 x a (5-2-16) 4、用分离变量法分离出两个常微分方程: 令 (x, y) = f (x) g( y) (5-2-17) 14 15
第五章则(5-2-12)变成两个方程151 d'f2k.(5-2-18)解为三角函数f dx?均为一次线性式。id'gP解为双曲函数(5-2-1 9-k1或实指数函数g dy26k2+k2=0(5-2-2 0)5、求通解:k22<0;k山<0 >0kx=0k=0V92025/6/1113电磁场理论
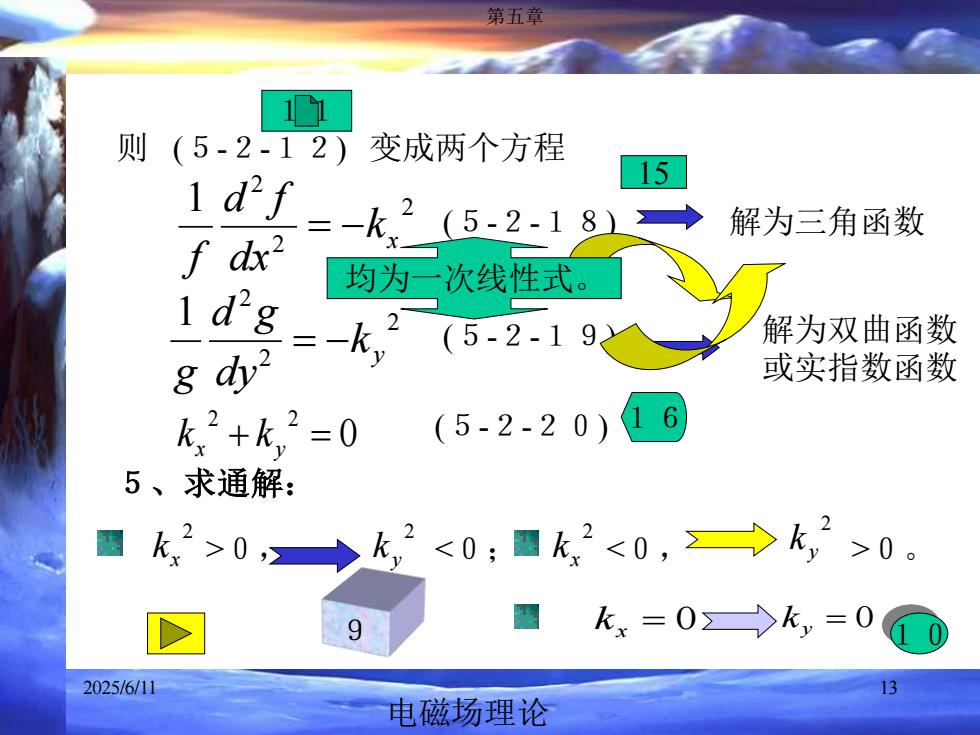
电磁场理论 2025/6/11 第五章 13 则 (5-2-12) 变成两个方程 2 2 2 1 x k dx d f f = − (5-2-18) 2 2 2 1 y k dy d g g = − (5-2-19) 0 2 2 kx + ky = (5-2-20) 11 5、求通解: 2 x k >0, 2 y k <0; 9 解为三角函数 解为双曲函数 或实指数函数 2 x k >0。 2 y k <0, 10 均为一次线性式。 16 kx = 0 ky = 0 15

第五章6、特解:(结合具体边界条件)1)分析:a.由(5-2-13)、(5-2-14),x=0,x=α,Φ=0A(5-2-1 8)的解f(x)只能取三角函数,即通解中的三种情况只有第一种是可以存在的:y=0,Φ=0由(5-2-1 5),b.::(5-2-1 9)的解g(y)只能取双曲函数2) 通解:f(x)= Asin k,x+A cosk,x (5-2-2 1)g(y) = B'sha,y+ B'cha,y(5-2-22142025/6/11电磁场理论
电磁场理论 2025/6/11 第五章 14 6、特解: (结合具体边界条件) 1) 分析: 12 a. 由(5-2-13)、(5-2-14), x = 0,x = a, = 0 (5-2-18)的解 只能取三角函数,即通解中的三种 情况只有第一种是可以存在的. f (x) b. 由(5-2-15), y = 0, = 0 (5-2-19)的解 只能取双曲函数. g( y) 2) 通解: f x A k x A k x x x ( ) sin cos 1 2 = + g y B sha y B cha y 1 y 2 y ( ) = + (5-2-21) (5-2-22)

第五章Ud(x,y) = f(x)·g(y)3)特解:d(x)=0a. f(x)f(x) = A sin k,x + A cosk,x: x=0,Φ=0=f(0)=0=A=0x=a,Φ=0=f(a)=0=Asinka=0;则k.α=nπ(n = 1,2,3......)n元即kx(5-2-23)二(n = 1,2,3......aon元故f(x)=(n = 1,2,3.....)sin(5-2-24xan=11312n元其中 sinx称为方程(5-2-18)满足(5-2-13)an元本征值(5-2-14)k.边界条件的本征函数.q2025/6/1115电磁场理论
电磁场理论 2025/6/11 第五章 15 3) 特解: (x, y) = f (x) g( y) a. f (x) f (x) = A1 sin kx x + A2 cos kx x 0, 0 (0) 0 0; x = = f = A2 = , 0 ( ) 0 sin 0; x = a = f a = A1 kx a = 则 k a n (n 1,2,3 ) x = = 即 故 (n 1,2,3 ) a n kx = = (5-2-23) x (n 1,2,3 ) a n f x A n = n = = ( ) sin 1 (5-2-24) 其中 x a n sin 称为方程 (5-2-18) 满足 (5-2-13) (5-2-14) 边界条件的本征函数. a n kx = 本征值 (x) = 0 13 12