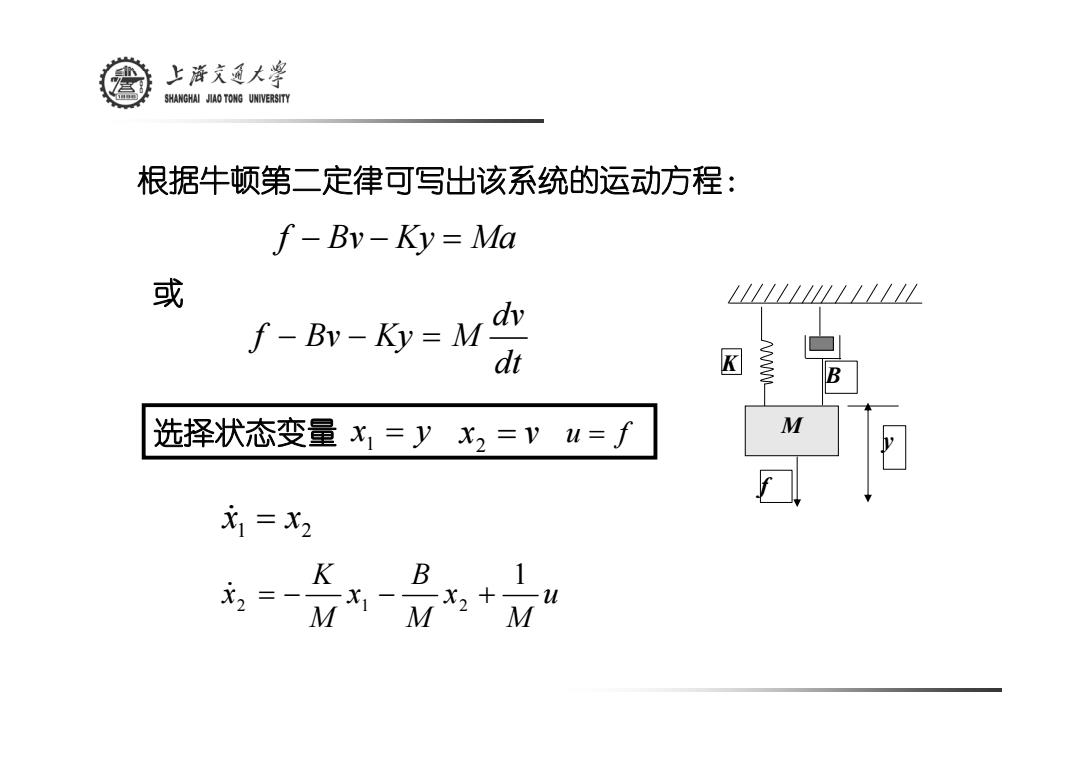
上文大学 SHANGHAI JIAO TONG UNIVERSITY 根据牛顿第二定律可写出该系统的运动方程: f-Bv-Ky=Ma 或 11111L///11 dv f-Bv-Ky=M dt 选择状态变量x1=yx2=yu=∫ M x1=X2 K B 1 2=一 M 2+ M M
x = y 1 x = v 2 u = f 根据牛顿第二定律可写出该系统的运动方程: dt dv f − Bv − Ky = M u M x M B x M K x 1 & 2 = − 1 − 2 + f − Bv − Ky = Ma 或 选择状态变量 1 2 x & = x K M B y f
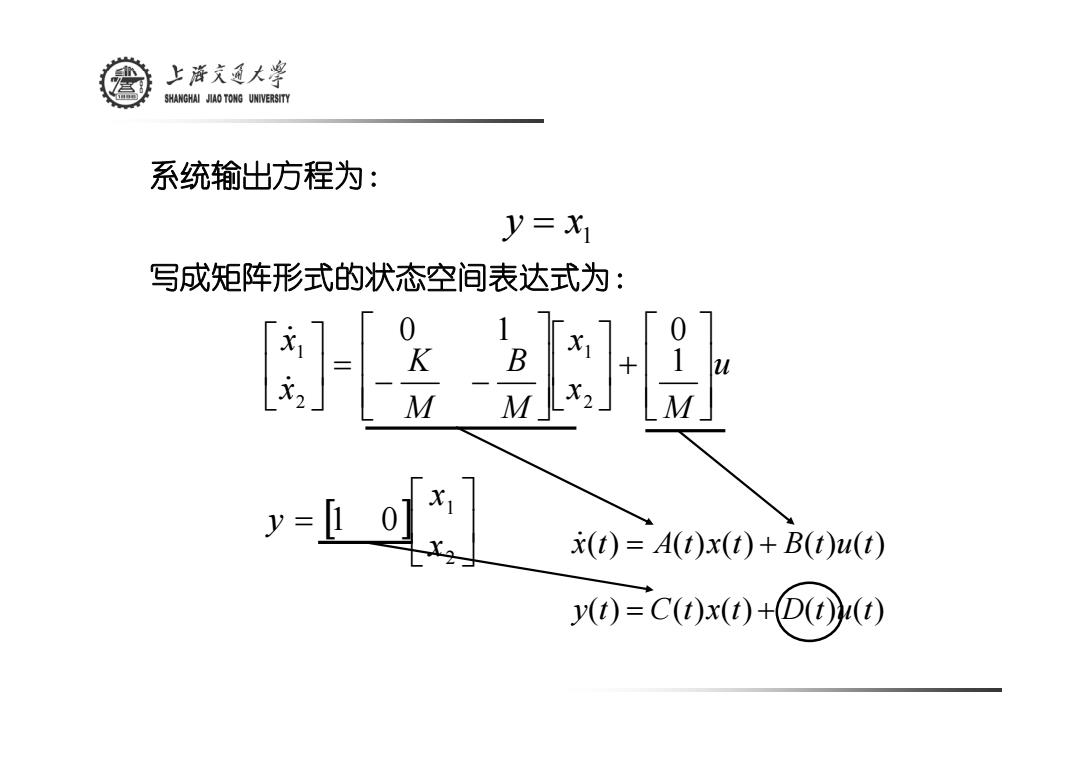
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 系统输出方程为: y=X 写成矩阵形式的状态空间表达式为: (t)=A(t)x(t)+B(t)u(t) ()=C()x()+D(t)
系统输出方程为: 写成矩阵形式的状态空间表达式为: 1 y = x [ ] ⎥⎦⎤ ⎢⎣⎡ = 21 1 0 xx y u M x x M B M K x x ⎥⎥⎦⎤ ⎢⎢⎣⎡ ⎥ +⎦⎤ ⎢⎣⎡⎥⎥⎦⎤ ⎢⎢⎣⎡− − ⎥ = ⎦⎤ ⎢⎣⎡ 1 0 1 0 21 21 && x &() () () () () t At xt Btut = + y() () () () () t Ctxt Dtut = +

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 2.3由传递函数求状态空间模型 经典控制理论:输入、输出变量间的传递函数描述系统 现代控制理论:输入、状态、输出变量间的一阶微分 方程组描述系统 模型计算步骤:需选取合适的状态变量,推导出状态空 间表达式,保持原输入输出关系不变 前提:G(s)可实现的充分必要条件是G(s)正则(分母阶次〉= 分子阶次)
经典控制理论:输入、输出变量间的传递函数描述系统 现代控制理论:输入、状态、输出变量间的一阶微分 方程组描述系统 模型计算步骤:需选取合适的状态变量,推导出状态空 间表达式,保持原输入输出关系不变 前提:G(s)可实现的充分必要条件是G(s)正则(分母阶次>= 分子阶次) 2.3 由传递函数求状态空间模型