
Chapter 6 Control of Stable Plants 4口,+@,4定4=定0C Zhang.W.D..CRC Press.2011 Version 1.0 1/74
Chapter 6 Control of Stable Plants Zhang, W.D., CRC Press, 2011 Version 1.0 1/74

Control of Stable Plants 16.1 The Quasi-Ho Smith Predictor 26.2 The H2 Optimal Controller and the Smith Predictor 36.3 Equivalents of the Optimal Controller 46.4 The PID Controller and High-Order Controllers 56.5 Choice of Weighting Functions 66.6 Simplified Tuning for Quantitative Robustness 4口,+@,4定4定90C Zhang.W.D..CRC Press.2011 Version 1.0 2/74
Control of Stable Plants 1 6.1 The Quasi-H∞ Smith Predictor 2 6.2 The H2 Optimal Controller and the Smith Predictor 3 6.3 Equivalents of the Optimal Controller 4 6.4 The PID Controller and High-Order Controllers 5 6.5 Choice of Weighting Functions 6 6.6 Simplified Tuning for Quantitative Robustness Zhang, W.D., CRC Press, 2011 Version 1.0 2/74

Section 6.1 The Quasi-Ho Smith Predictor 6.1 The Quasi-Ho Smith Predictor Chapter 4 and Chapter 5:The controller is analytically designed by minimizing the weighted sensitivity function This section:The controller is analytically designed by specifying the desired closed-loop response Actually,a simplified version of this method was already used in Sections 5.5 and 5.6 Consider the diagram of the Smith predictor in Figure,where G(s) is the plant,G(s)is its model,and Go(s)is the delay-free part of G(s).If the closed-loop transfer function T(s)is known,the controller of the Smith predictor is T(s) R(s)= G(s)-T(s)Go(s) 4口,+@,4定4=定0C Zhang.W.D..CRC Press.2011 Version 1.0 3/74
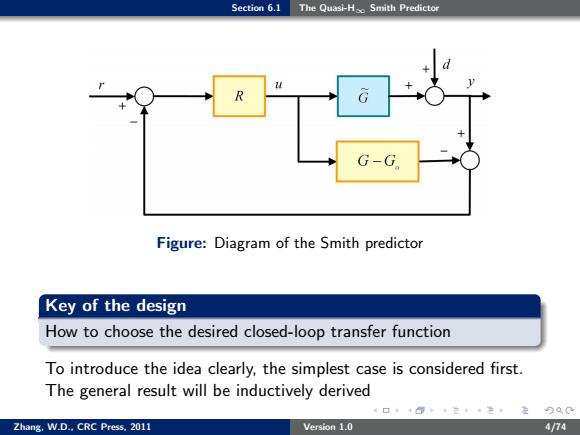
Section 6.1 The Quasi-H∞ Smith Predictor 6.1 The Quasi-H∞ Smith Predictor Chapter 4 and Chapter 5: The controller is analytically designed by minimizing the weighted sensitivity function This section: The controller is analytically designed by specifying the desired closed-loop response Actually, a simplified version of this method was already used in Sections 5.5 and 5.6 Consider the diagram of the Smith predictor in Figure, where G˜ (s) is the plant, G(s) is its model, and Go(s) is the delay-free part of G(s). If the closed-loop transfer function T(s) is known, the controller of the Smith predictor is R(s) = T(s) G(s) − T(s)Go(s) Zhang, W.D., CRC Press, 2011 Version 1.0 3/74

Section 6.1 The Quasi-Ho Smith Predictor 6.1 The Quasi-Ho Smith Predictor Chapter 4 and Chapter 5:The controller is analytically designed by minimizing the weighted sensitivity function This section:The controller is analytically designed by specifying the desired closed-loop response Actually,a simplified version of this method was already used in Sections 5.5 and 5.6 Consider the diagram of the Smith predictor in Figure,where G(s) is the plant,G(s)is its model,and Go(s)is the delay-free part of G(s).If the closed-loop transfer function T(s)is known,the controller of the Smith predictor is T(s) R(6)=G(3)-T(s)G.(5) 4口,+@,4定4=定0C Zhang.W.D..CRC Press.2011 Version 1.0 3/74
Section 6.1 The Quasi-H∞ Smith Predictor 6.1 The Quasi-H∞ Smith Predictor Chapter 4 and Chapter 5: The controller is analytically designed by minimizing the weighted sensitivity function This section: The controller is analytically designed by specifying the desired closed-loop response Actually, a simplified version of this method was already used in Sections 5.5 and 5.6 Consider the diagram of the Smith predictor in Figure, where G˜ (s) is the plant, G(s) is its model, and Go(s) is the delay-free part of G(s). If the closed-loop transfer function T(s) is known, the controller of the Smith predictor is R(s) = T(s) G(s) − T(s)Go(s) Zhang, W.D., CRC Press, 2011 Version 1.0 3/74
Section 6.1 The Quasi-Ho Smith Predictor R G G-G Figure:Diagram of the Smith predictor Key of the design How to choose the desired closed-loop transfer function To introduce the idea clearly,the simplest case is considered first. The general result will be inductively derived 定00 Zhang.W.D..CRC Press.2011 Version 1.0 4/74
Section 6.1 The Quasi-H∞ Smith Predictor Figure: Diagram of the Smith predictor Key of the design How to choose the desired closed-loop transfer function To introduce the idea clearly, the simplest case is considered first. The general result will be inductively derived Zhang, W.D., CRC Press, 2011 Version 1.0 4/74