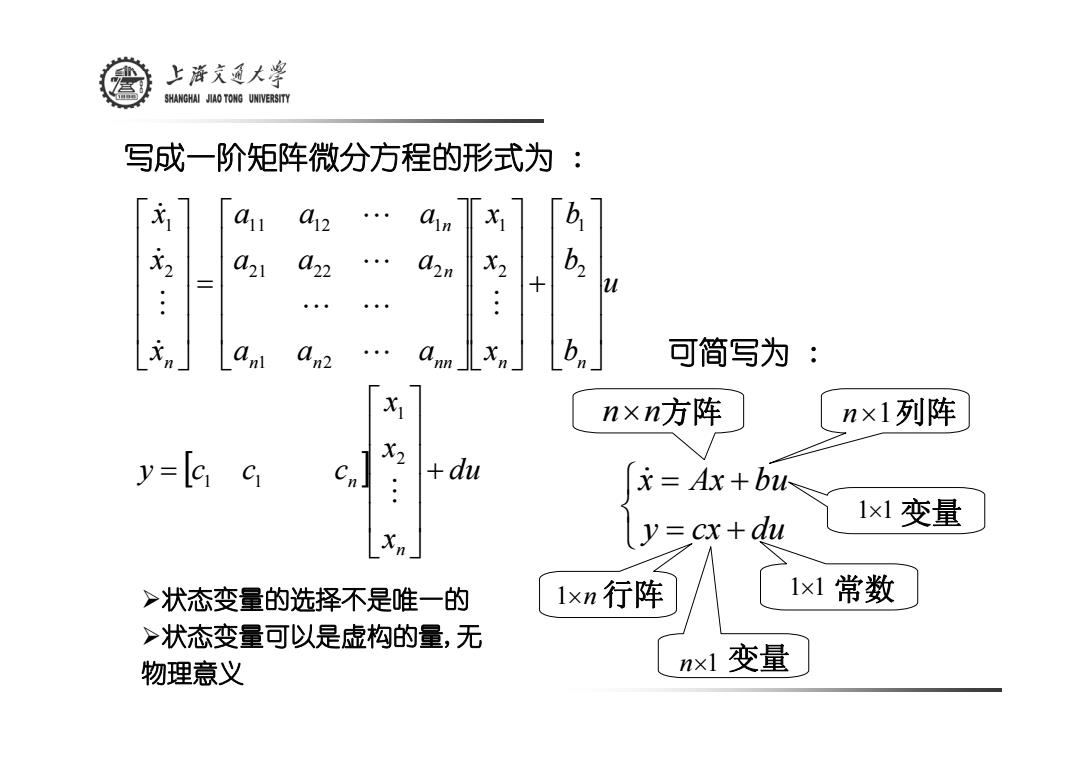
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 写成一阶矩阵微分方程的形式为 元1 a12 b 元2 021 022 02n X2 b2 三 An2 xn」 可简写为: n×n方阵 n×1列阵 y=c a X2 Cn .: du =Ax+bu y=cx+du 1x1变量 >状态变量的选择不是唯一的 1xn行阵 1x1常数 >状态变量可以是虚构的量,无 物理意义 nx1变量
写成一阶矩阵微分方程的形式为 : [ ] du x x x y c c c u b b b x x x a a a a a a a a a x x x n n n n nn n n n n n + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ M M L L L L L & M & & 2 1 1 1 2 1 2 1 1 2 21 22 2 11 12 1 2 1 变量 n × n方阵 1 × n 行阵 n × 1列阵 1 × 1 常数 ⎩ ⎨ ⎧ = + = + y cx du x& Ax bu 1 × 1 变量 n × 1 可简写为 : ¾状态变量的选择不是唯一的 ¾状态变量可以是虚构的量,无 物理意义

上商文通大¥ SHANGHAI JIAO TONG UNIVERSITY 具有个输入和个输出的系统的状态方程一般形式为: x1=a11+a2x2+…+anxn+b24+b242+…+b,4, x2=a21x1+a22X2+…+a2nmXn+b2141+b2242+…+b2,u 元n=anX1+an2x2+…+AmXn+bni24+bn242+…+bnm4, 输出方程的一般形式为: y=Cx+C12x2+…+Cmxn+d1h1+d12W2+…+d,u, y2=C211+C22X2+…+C2mXn+d2i41+d2u2+…+d2,, ym Cm+Cm2X2++Cmnx +dmu +dm2u2++dmur
具有r个输入和m个输出的系统的状态方程一般形式为: n n n nn n n n nr r n n r r n n r r x a x a x a x b u b u b u x a x a x a x b u b u b u x a x a x a x b u b u b u = + + + + + + + = + + + + + + + = + + + + + + + & L L LL & L L & L L 1 1 2 2 1 1 2 2 2 21 1 22 2 2 21 1 22 2 2 1 11 1 12 2 1 11 1 12 2 1 m m m mn n m m mr r n n r r n n r r y c x c x c x d u d u d u y c x c x c x d u d u d u y c x c x c x d u d u d u = + + + + + + + = + + + + + + + = + + + + + + + L L LL L L L L 1 1 2 2 1 1 2 2 2 21 1 22 2 2 21 1 22 2 2 1 11 1 12 2 1 11 1 12 2 1 输出方程的一般形式为:
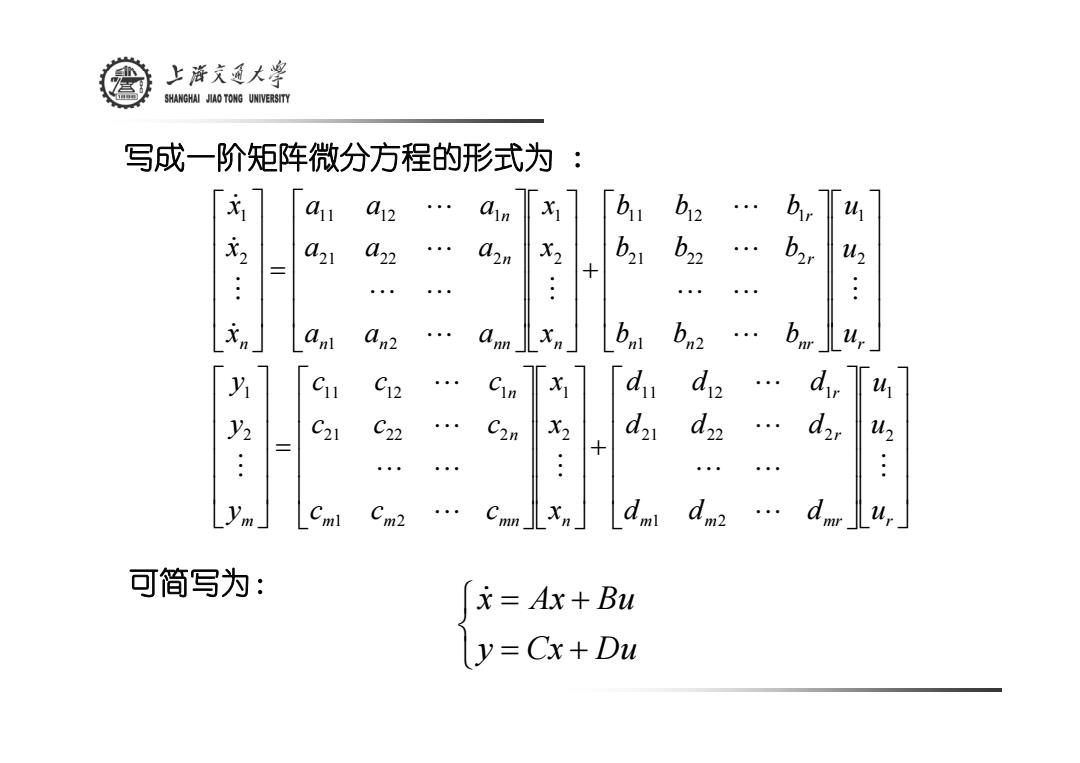
上文大学 SHANGHAI JIAO TONG UNIVERSITY 写成一阶矩阵微分方程的形式为 无 a12 n 元2 01 02 02n X2 b21 b22 bzr Uz . .: an an2 bn 为 C11 C12 X d u 2 C21 C22 C2n x2 d2 d uz 三 . + .: ym Cml Cm2 Cmn dm … u, 可简写为: =Ax+Bu y=Cx+Du
⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ m m mr r r r m m mn n n n m n n nr r r r n n nn n n n n u u u d d d d d d d d d x x x c c c c c c c c c y y y u u u b b b b b b b b b x x x a a a a a a a a a x x x M L L L L L M L L L L L M M L L L L L M L L L L L & M & & 2 1 1 2 21 22 2 11 12 1 2 1 1 2 21 22 2 11 12 1 2 1 2 1 1 2 21 22 2 11 12 1 2 1 1 2 21 22 2 11 12 1 2 1 可简写为: 写成一阶矩阵微分方程的形式为 : ⎩ ⎨ ⎧ = + = + y Cx Du x& Ax Bu

上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 口建立状态空间模型的步骤: 1)选择合适的状态变量 2)根据系统物理机理或其他方面的机理列写微分方程, 化成一阶微分方程组 3)写成矩阵形式,得到状态空间模型 ▣建立状态空间模型的常用方法: 1)采用机理分析法建模 2)根据系统传递函数建模
建立状态空间模型的步骤: 1) 选择合适的状态变量 2) 根据系统物理机理或其他方面的机理列写微分方程, 化成一阶微分方程组 3) 写成矩阵形式, 得到状态空间模型 建立状态空间模型的常用方法: 1) 采用机理分析法建模 2) 根据系统传递函数建模
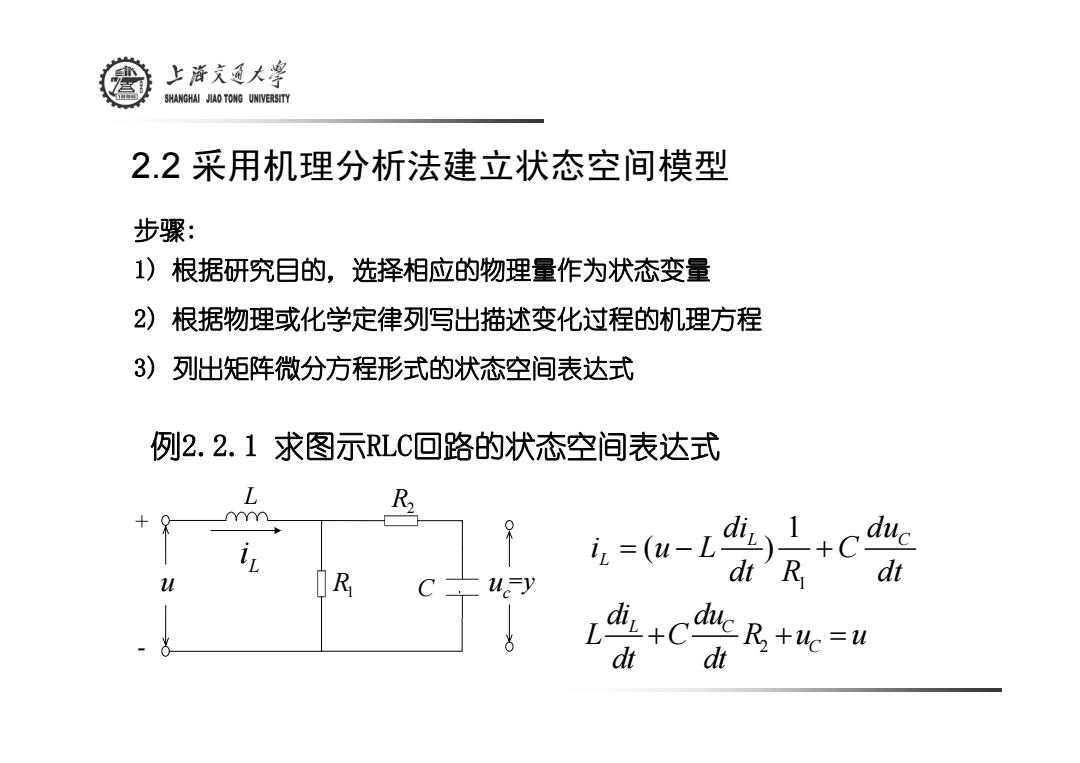
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 2.2采用机理分析法建立状态空间模型 步骤: 1)根据研究目的,选择相应的物理量作为状态变量 2)根据物理或化学定律列写出描述变化过程的机理方程 3)列出矩阵微分方程形式的状态空间表达式 例2.2.1求图示RLC回路的状态空间表达式 L R i.=(u- d)1+ duc dt u R uy R diL+C dt duc R+uc=u dt
2.2 采用机理分析法建立状态空间模型 步骤: 1) 根据研究目的,选择相应的物理量作为状态变量 2) 根据物理或化学定律列写出描述变化过程的机理方程 3) 列出矩阵微分方程形式的状态空间表达式 1 1 ( ) L C L di du i uL C dt R dt =− + 2 L C C di du L C Ru u dt dt + + = 例2.2.1 求图示RLC回路的状态空间表达式 u L c u R2 R1 Li + - C =y