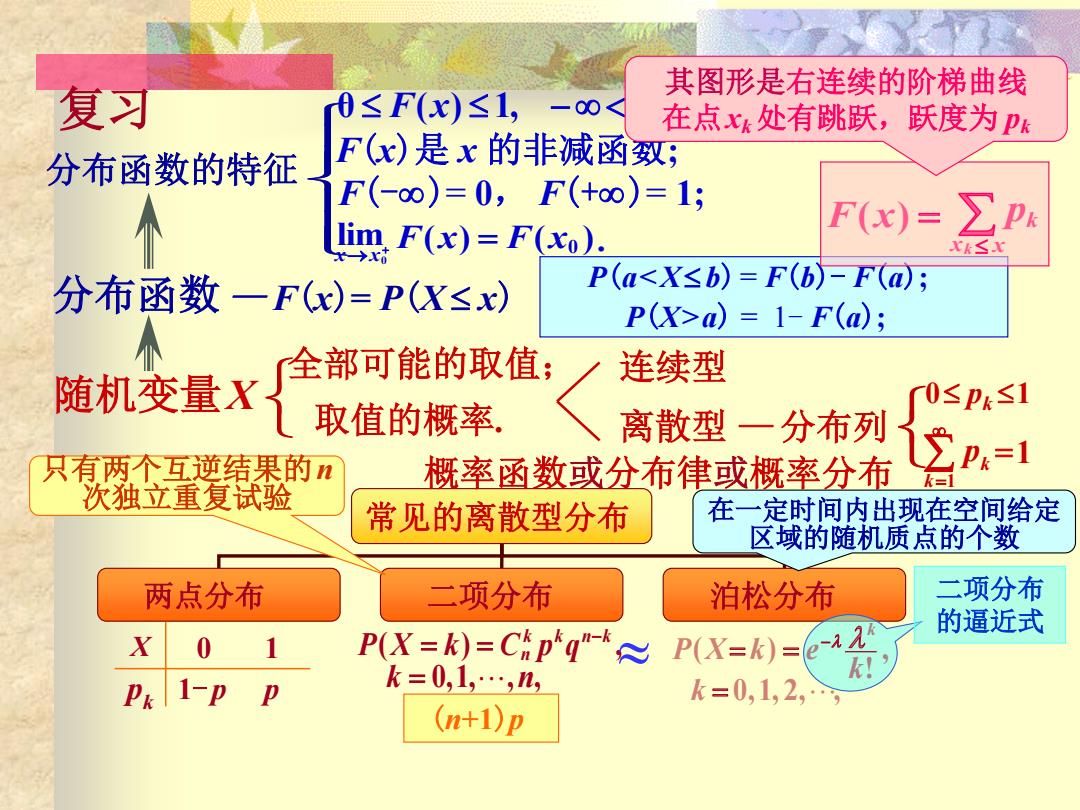
其图形是右连续的阶梯曲线 复习 0≤F(x)≤1, 一0< 在点x处有跳跃,跃度为Pk 分布函数的特征 F(x)是x的非减函致 F(-o0)=0,F(+o∞)=1; lim,F(x)=F(xo) F(x)= ∑Pk Xk≤X 分布函数一F(x)=P(X≤x) P(a<X≤b)=F(b)-F(d; P(X>a)=1-F(a); 全部可能的取值; 连续型 随机变量X 取值的概率. 0≤Pk≤1 离散型一分布列 只有两个互逆结果的n 概率函数或分布律或概率分布 P=1 k= 次独立重复试验 常见的离散型分布 在一定时间内出现在空间给定 区域的随机质点的个数 两点分布 二项分布 泊松分布 二项分布 的逼近式 X 0 P(X=k)=Cpq"-≈ P(X=k)=-a2 Pk 1-P p k=0,1,…,n, k=0,1,2, (n+1)p
常见的离散型分布 两点分布 二项分布 泊松分布 0,1, 2, , , ! ( ) k k P X k e k 全部可能的取值; 取值的概率. 随机变量X —分布列 分布函数 概率分布与分布函数的关系? 复习 连续型 离散型 分布函数的特征 概率函数或分布律或概率分布 — F(x)= P(X x) 0 pk 1 0 F(x) 1, x ; F(-)= 0, F(+)= 1; F(x)是 x 的非减函数; P(a<X b) = F(b)- F(a); P(X>a) = 1- F(a); 1 1 k k p ( ) ( ). lim 0 0 F x F x x x 0,1, , , ( ) , k n P X k C p q k k n k n X 0 1 pk 1- p p 只有两个互逆结果的n 次独立重复试验 (n+1)p 二项分布 的逼近式 x x k k F(x) p 其图形是右连续的阶梯曲线 在点xk 处有跳跃,跃度为 pk 在一定时间内出现在空间给定 区域的随机质点的个数

我们介绍了离散型随机变量及其概率分布 只要知道了随机变量的分布函数,就可以计算与 该随机变量有关的事件的概率. 对于离散型随机变量,如果知道了它的分布列, 也就知道了该随机变量取值的概率规律.在这个意义 上,我们说离散型随机变量由它的分布列唯一确定. 下面,我们将向大家介绍另一种类型的随机变量 连续型随机变量的描述方法
在这个意义 上,我们说 对于离散型随机变量,如果知道了它的分布列, 也就知道了该随机变量取值的概率规律. 离散型随机变量由它的分布列唯一确定. 下面,我们将向大家介绍另一种类型的随机变量 我们介绍了离散型随机变量及其概率分布. 只要知道了随机变量的分布函数,就可以计算与 该随机变量有关的事件的概率. —— 连续型随机变量的描述方法

§2.3连续型随机变量 不能象离散型那样,以指定它取每个 值的概率的方式去给出其概率分布 全部可能取值有无穷多,而且充满一个(或若干)区间而不能 一列举 类似于前面对离散型随机变量的讨论,对于连续型随机变 量我们首先关心的是:如何描述它取值的概率规律 分布函数?其取值的概率规律 例1:设有一质点等可能地落入区间[0,2]内, 令X为落 入后这个质点到原点O的距离,求X的分布函数. 解显然X为随机变量,且可能取值充满了区间[0,2], 当x<0时,F(x)=PX≤x)=P(D)=0; 当0≤x<2时,F(x)=P(X≤x)=x/2; 当x≥2时,F(x)=P(X≤)=1. 0, x<0; 故X的分布函数为F(x)={x/2,0≤x<2; 连续函数 F'w)=f)=V2, 0≤x<2; 1,x≥2. 0, 其他. 非负函数可积 =F(x)-F(-o)=∫nft)dt
: 令X为落 入后这个质点到原点 O 的距离, F(x) 解 显然 X 为随机变量, §2.3 连续型随机变量 全部可能取值有无穷多,而且充满一个(或若干)区间而不能一一列举 类似于前面对离散型随机变量的讨论,对于连续型随机变 量我们首先关心的是: 分布函数 其取值的概率规律 例 1 如何描述它取值的概率规律. ? 设有一质点等可能地落入区间[0, 2]内, 求 X 的分布函数. 且可能取值充满了区间[0, 2], 当 x<0 时,F(x)= P(X x) 故 X 的分布函数为 = P( )= 0; 当 0 x<2 时, F(x)= P(X x) = x /2; 当 x2 时,F(x)= P(X x)= P(X<0)+P(0X2)+P(2<Xx) = 0 + 2/2 + 0 = 1. 1, 2. /2, 0 2; 0, 0; ( ) x x x x F x 0, . 1/ 2, 0 2; ( ) 其他 x f x x f (t)dt 非负函数 不能象离散型那样, 以指定它取每个 值的概率的方式去给出其概率分布 1 . . 0 1 2 x F . F(x) F() 可积 连续函数
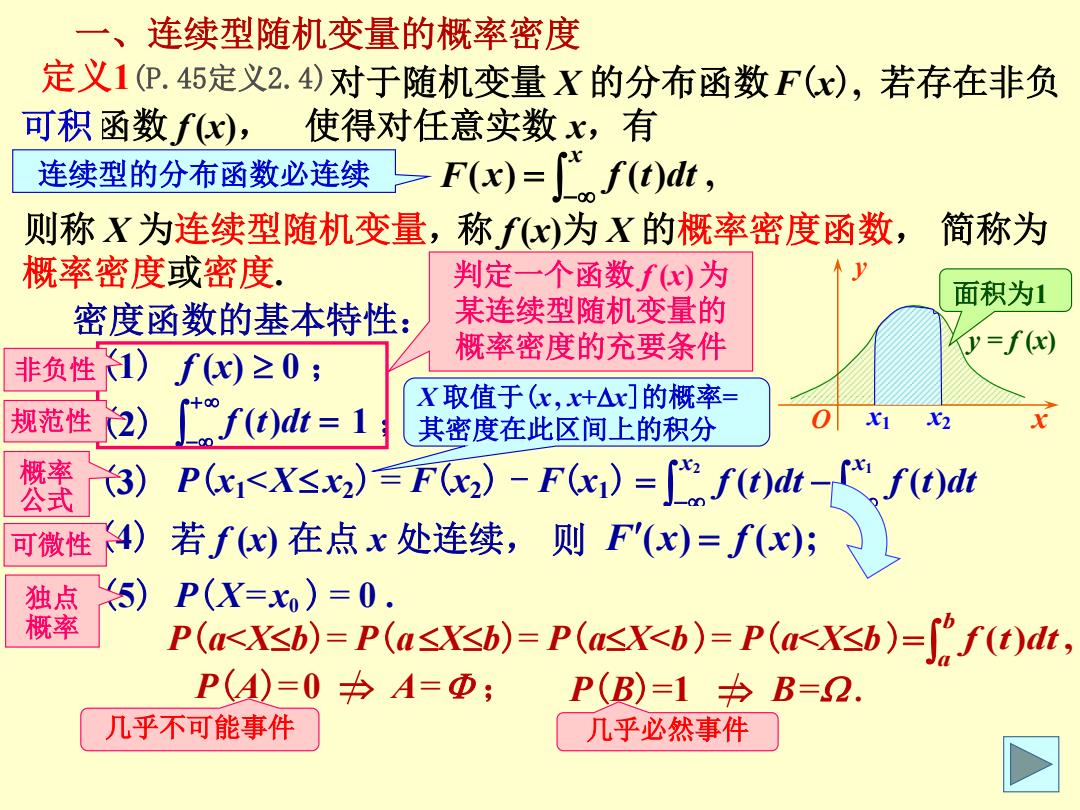
一、连续型随机变量的概率密度 定义1(P.45定义2.4)对于随机变量X的分布函数F(x),若存在非负 可积函数fx),使得对任意实数x,有 连续型的分布函数必连续 -F(x)=f(t)dt, 则称X为连续型随机变量,称f)为X的概率密度函数,简称为 概率密度或密度. 判定一个函数fx)为 面积为1 密度函数的基本特性: 某连续型随机变量的 概率密度的充要条件 =f) 非负性1) fx)≥0; X取值于(x,+△x]的概率= 规范性 2) [f(t)dt=1 其密度在此区间上的积分 率 公式 3) P(c1<X≤x )F)-Fx)=f(di-f(t)d 可微性 4) 若fx)在点x处连续,则F'(x)=f(x); 独 5) P(X=x)=0. 率 P(aKXb)=P(a≤Xb)=P(a≤XKb)=P(aKX≤b)=∫f(t)dt P(A)=0A=Φ; P(B)=1≠B=2. 几乎不可能事件 几乎必然事件
2 1 ( ) ( ) x x f t dt f t dt 简称为 概率密度或密度. 对于随机变量 X 的分布函数F(x), 若存在非负 可积函数 f (x), ( ) ( ) , x F x f t dt 使得对任意实数 x,有 则称 X 为连续型随机变量, 由定义 一、连续型随机变量的概率密度 称 f (x)为 X 的概率密度函数, 定义1(P.45定义2.4) 密度函数的基本特性: (1) f (x) 0 ; ( ) ( ) ( ) (2) f t dt F 1 ; F = 1 - 0 (3) P(x1<X x2) = F(x2) - F(x1) (4) (5) = 0 判定一个函数 f (x)为 某连续型随机变量的 概率密度的充要条件 独点 概率 非负性 规范性 可微性 概率 公式 y O x y = f (x) 面积为1 x1 x2 ( ) ; 2 1 x x f t dt 2 1 1 1 ( ) ( ) ( ) x x x x 若 f (x) 在点 x 处连续, f t dt 则 Ff(xt)dt f (x)f; t dt lim ( 0 0 ) 0 P x X x x x x x x x f x dx 0 0 lim ( ) 0 P(X=x0 ) = 0 . P(a<Xb)= P(aXb)= P(aX<b )= P(a<Xb ) ( ) , b a f t dt 几乎不可能事件 几乎必然事件 P(A)=0 A= ; P(B)=1 B= . X 取值于(x , x+x]的概率= 其密度在此区间上的积分 可积 连续型的分布函数必连续

对fx)的进一步理解: 若x是f(x)的连续点,则 质 lim P(x<X≤x+)= lim f)d lim f(x+4x)=f(x) 4c→0 △x r→0 ∠K r→0 这表明X的密度fx)在x这一点的值,恰好是X落在区间 (x,x+△x]上的概率与区间长度△x之比的极限.如果我们把概率 理解为质量,则f)相当于线密度. 由极限概念知P(x<X≤x+x)≈f(x),它表明随机变量X 取值于区间(x,x+△]的概率近似等于fx)△x;这表明fx)△x在连 续型随机变量理论中所起的作用与P{X=xx}=Pk在离散型随机变 量理论中所起的作用相类似. 注意,密度函数fc)在某点处的值,并不等于X取值的概 率.但这个值越大,则X取a附近的值的概率就越大. 即在某点 密度曲线的高度反映了概率集中在该点附近的程度. 连续型随机变量由它的密度函数所唯一确定.所以,若已知密 度函数,该连续型随机变量的概率规律就得到了全面描述
所以,若已知密 度函数,该连续型随机变量的概率规律就得到了全面描述. 即在某点 密度曲线的高度反映了概率集中在该点附近的程度. 注意,密度函数 f (x) 在某点 a 处的值,并不等于 X 取值的概 率. 这表明 f (x)x 在连 续型随机变量理论中所起的作用与 P{ X= xk}= pk 在离散型随机变 量理论中所起的作用相类似. 它表明随机变量 X 取值于区间(x, x+x]的概率近似等于 f (x)x; 但这个值越大,则 X 取 a 附近的值的概率就越大. 如果我们把概率 理解为质量, 恰好是 X 落在区间 ( x , x+x]上的概率与区间长度 x 之比的极限. 这表明 X 的密度 f (x) 在 x 这一点的值, 若 x 是 f (x) 的连续点,则 x P x X x x x ( ) lim 0 x f t dt x x x x ( ) lim 0 = f (x) 对 f (x) 的进一步理解: lim ( ) 0 f x x x 则 f (x) 相当于线密度. 由极限概念知 P( x X xx) f (x)x , 质量 连续型随机变量由它的密度函数所唯一确定