
例2(P.47例2)设随机变量X的概率密度为 A(4x-2x2),0<x<2; ={ (1)确定常数A; 0, 其它, (2)求X的分布函数F(x); (3)求P(0≤X<1),PX1) 解()1=gfdi=0dc+44x-2x2+店0dk=3A,A=g ②))由(①知f=是r-2,0<2: 由概率密度定义知 0. 其它, F()=f()t, 当x<0时,F(x)=0dt=0; 0 x≤0; 当un-产2 当x≥2时,F()=0dt+6(: 1 X≥2. (3) 用分布函数求 用概率密度求 P(0≤X<1)=F(1)-F(O)=7, P0≤X<)=2x-x2)=2 P(X1)=1-F(1)=2: P1)=(x-x2)dx=2
例2(P.47 例2) 设随机变量 X 的概率密度为 0, , (4 2 ), 0 2; ( ) 2 其它 A x x x f x (1) 确定常数A; (2) 求X 的分布函数F(x); 解(1) 1 f (t)dt 2 2 0 2 0 0dx A(4x 2x )dx 0dx , 3 8 A (3) 求 P(0X<1), P(X>1). . 8 3 A 由概率密度定义知 ( ) ( ) , x F x f t dt 当 x<0 时, 当 0<x<2 时, 当 x2 时, x F x dt t t dt 0 2 0 ) 4 3 2 3 ( ) 0 ( (2) 由(1)知 0, , , 0 2; 4 3 2 3 ( ) 2 其它 x x x f x 2 4 3 ; 1 4 3 x x x F x dt t t dt dt 2 2 0 2 0 ) 0 4 3 2 3 ( ) 0 ( = 1, 1, 2 . , 0 2 4 1 4 3 0, 0; ( ) 2 3 x x x x x F x ; (3) 由密度函数的概率公式知 用分布函数求 ( ) 0 0; x F x dt 0 2 1 , P(X>1)=1-PF((1) X1) 2 1 1. 2 1 P(0X<1)= F(1)-F(0) , 2 1 1 P(X 1) f (x)dx . 2 1 2 1 2 ) 4 3 2 3 ( x x dx 1 0 P(0 X 1) f (xx)dx x )dx 4 3 2 3 ( 2 用概率密度求
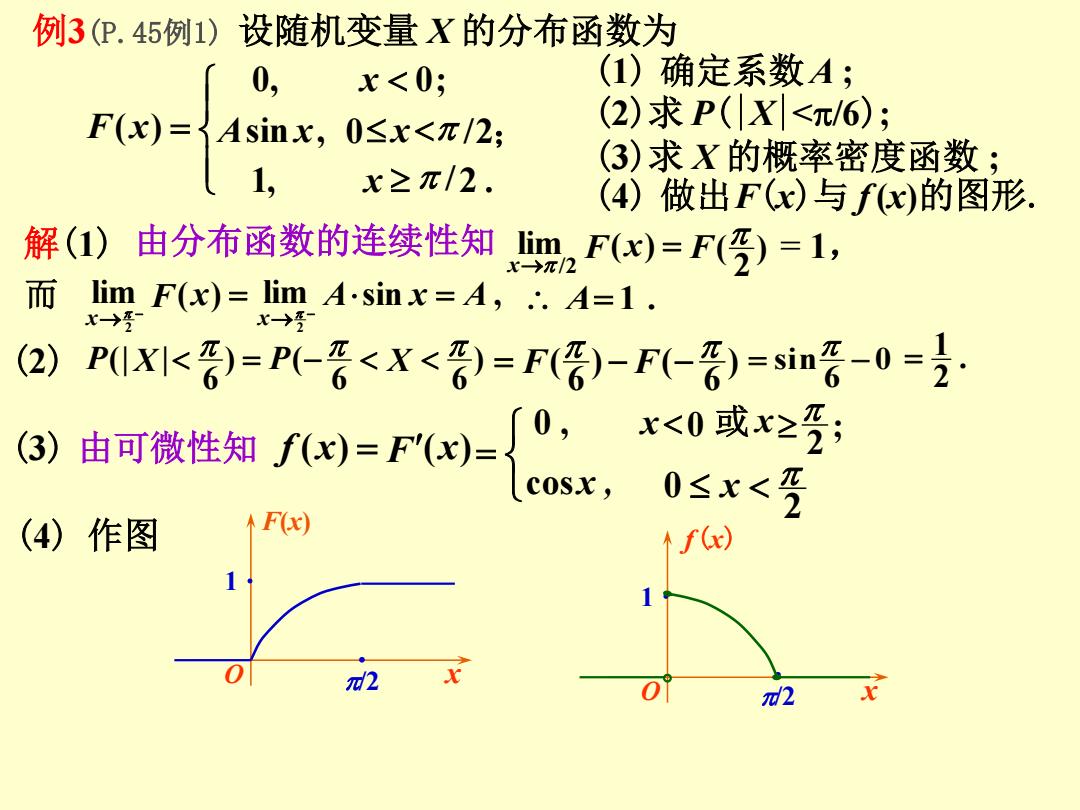
例3(P.45例1)设随机变量X的分布函数为 0, x<0; (1)确定系数A; F(x)=Asinx, 0≤x<π/2; (2)求P(X|<π/6); 1, (3)求X的概率密度函数; x≥π/2. (4)做出F(x)与fx)的图形 解(1)由分布函数的连续性知 Iim2F(x)=F()=1, x-→π/2 lim F(x)=lim A.sinx=A,.A=1. X→ X→ (2) P(XI<)=P(-若<X<)=F()-F(-)=sing-0=克: (3) 由可微性知f)=F(x)=厂0, x<0或x≥; cosx, 0≤x< (4)作图 F(x) f(r) n2 x2
例3(P.45例1) 设随机变量 X 的分布函数为 (1) 确定系数 A ; (2)求 P(|X|</6); 解(1) ) 2 lim ( ) ( /2 F x F x 0 6 sin (3)求 X 的概率密度函数 ; A 1 . 由分布函数的连续性知 ) 6 6 ) ( 6 (| | (2) P X P X ; 2 0 x 或 x ) 6 ) ( 6 ( F F = 1, 1, / 2 . sin , 0 /2 0, 0; ( ) x A x x x F x ; (3) 由可微性知 (4) 作图 . 2 1 0 , cosx , (4) 做出F(x)与 f (x)的图形. lim ( ) lim sin , 2 2 F x A x A x x 而 f (x) F(x) 2 0 x f(x) O x F(x) O x . /2 1 . /2 1

二、几个常见的连续型随机变量 1.均匀分布 假设连续型随机变量X在区间[4,b]上取值,且取值在[a,b]中 任意子区间内的概率仅与这个子区间的长度成正比,而与子区间的 位置无关,即X的取值在[α,b]上具有均等性. 定义1(P.49)若连续型随机变量X的概率密度为 可描述在某区间 上具有等可能 a≤r≤b; 结果的随机试验 0. 其它, f(x) 则称X在[4,b]上服从均匀分布,记作X~U[,b]. 均匀分布的分布函数: 0, x<a; F(d X-0 b-a a≤x<b; 1, x≥b, 典型应用:数值计算中由于小数点后某位小数四舍五入所引起的误差; 两辆公共汽车前后通过某停车站的时间(乘客候车时间)等
= 1 b a dt 而与子区间的 位置无关, f(x) a O b x [ ] 1. 均匀分布 则称 X在[a,b]上服从均匀分布, 0, , , ; 1 ( ) 其它 a x b b a f x 二、 几个常见的连续型随机变量 定义1(P.49) 若连续型随机变量 X 的概率密度为 且取值在[a ,b]中 任意子区间内的概率仅与这个子区间的长度成正比, 即 X 的取值在[a , b]上具有均等性. 假设连续型随机变量 X 在区间[a, b]上取值, 记作 X ~ U[a, b]. 均匀分布的分布函数: x F(x) f (t)dt x a ; a x b ; x a b a dt xb , , b a x a 0, 1 , x b b a dt b a dt 0 F(x) a O b x 1 ba 1 典型应用:数值计算中由于小数点后某位小数四舍五 入所引起的误差; 两辆公共汽车前后通过某停车站的时间(乘客候车时间)等. 可描述在某区间 上具有等可能 结果的随机试验

例4(P.50例5)设某公共汽车站每10分钟有一班车通过,则在任 一时刻到站乘客的候车时间X(单位:分钟)在区间[0,10]上服从均匀 分布,试求乘客候车时间超过6分钟的概率. 解:X~U[a,f时=品, 0≤x≤10; 0, 其它, 所求概率为P{X>6}=”fx)=公k=号. 例5(P.59Ex11)设随机变量X~U[2,5],现对X进行三次独立观测, 求至少有两次观测值大于3的概率. 解XU[2,5,f=得2≤x≤5 则P{X>3}=∫310d=号 0, 其它, 设Y表示对X的观测值大于3的次数,Y=0,1,2,3,则Y~B(3,23), 所求概率为P(P>2)=店P=)=含C2/31V3=费
则在任 一时刻到站乘客的候车时间 X(单位: 分钟)在区间[0, 10]上服从均匀 分布, 解 ∵ X ~U[a, b], 所求概率为 0, 其它, , 0 10; 10 1 ( ) x f x 例4(P.50 例5) 设某公共汽车站每 10 分钟有一班车通过, 试求乘客候车时间超过 6 分钟的概率. P{X 6} f x dx 6 ( ) dx 10 6 10 1 . 5 2 例5(P.59EX11) 设随机变量X~U[2, 5],现对X进行三次独立观测, 求至少有两次观测值大于 3 的概率. 解 ∵ X~U[2, 5], 0, 其它, , 2 5; 3 1 ( ) x f x 则 P{X3} dx 5 3 10 1 . 3 2 设Y表示对X的观测值大于3的次数,Y=0,1, 2, 3,则 Y~B(3, 2/3), 所求概率为 P(Y 2) 3 2 ( ) k P Y k k k k k C 3 3 2 3 (2 / 3) (1/ 3) . 27 20

2.指数分布 定义2若连续型随机变量X的概率密度为 f(x)= [e-, x>0; f(r) 0, x≤0, 其中兄>0为常数,则称X服从参数为入的指数分布, 记为X~E(2). F(x) 指数分布的分布函数: F) x≤0; 0 X 指数分布在可靠性理论中描绘设备工作的可靠时间.有些系统的寿命分布也 可用指数分布来近似,如电子产品或动物寿命的分布,当产品的失效是偶然失效 时其寿命服从指数分布.在排队论中它被广泛地用于描绘等待时间,如电话通 话时间、各种随机服务系统的服务时间、等待时间等.在更新和维修问题中描 绘设备的寿命和维修时间.指数分布是伽玛分布和威布尔分布的特殊情况. 一般地,当随机质点流中在长的时间内出现的质点数服从参数为t的泊松 分布时,其相继出现两个质点的事件间就服从参数为入的指数分布
在更新和维修问题中描 绘设备的寿命和维修时间. 如电话通 话时间、各种随机服务系统的服务时间、等待时间等. 当产品的失效是偶然失效 时其寿命服从指数分布. 在排队论中它被广泛地用于描绘等待时间, 指数分布是伽玛分布和威布尔分布的特殊情况. 有些系统的寿命分布也 可用指数分布来近似, 则称X服从参数为 的指数分布, 指数分布在可靠性理论中描绘设备工作的可靠时间. 其中>0为常数, 记为 X~E(). 2. 指数分布 指数分布的分布函数: F(x) x 0; 0, x 0; 0 , 0 0 x x dx e dx 1 , 0; e x x F(x) O x 1 如电子产品或动物寿命的分布, 一般地, 当随机质点流中在长t 的时间内出现的质点数服从参数为t 的泊松 分布时, 其相继出现两个质点的事件间就服从参数为的指数分布. 0 x e 0 dx = 1 0 x e 定义2 若连续型随机变量 X 的概率密度为 0, 0, 0 ( ) x e x f x x , ; f(x) O x