上海交通大学：《概率论与数理统计》课程教学资源（课件讲稿）08、多维随机变量及分布 §3.3 二维随机变量的条件分布 §3.4 随机变量的独立性

复习X与Y的联合分布F(x,y)=P{X≤x,Y≤y} P{1<X≤x2,y1<Y≤y2}=F(2,y2)-F(x2,JM1)+F(,1)-F(1,y2) 离散型一 联合分布列P{X=x,Y=yj=Pi,j=1,2,… 联 F(x,y)=P{X≤x,Y≤y}=∑P 分布 xi≤x,yi≤y 函数 连续型 联合概率密度 02F(x,y)=f(x,y) Oxoy F(x,y)=∫」f(u,v)dudw P((x,y)EG=(,y)dd X,)关于X和Y的边缘分布Fx(x)=F(x,o),F(y)=F(+o,y) 离散型一边缘分布列 关于x的PP=PX=iFx()P 边缘 分布 关于Y的p=PH=P{Y=y,F(x)=P ≤y 函数 关于X的fx(x)=f(x,y) 连续型 边缘概率密度 Fx(x)=∫f(u,y)y]u 关于y的f(y)=fx,y)k Fy(y)=f(x,v)dxldv

复习 联合 分布 函数    离散型 连续型 { , } ( , ) ( , ) ( , ) ( , ) P x1  X  x2 y1 Y  y2  F x2 y2 F x2 y1  F x1 y1 F x1 y2 —— 联合分布列 —— 联合概率密度 i j pij P{Xx , Y y } i, j 1,2,         x x y y ij i j F x y P X x Y y p , ( , ) { , }    y x F(x, y) f (u,v)dudv P x y G f x y dxdy f x y x y F x y G        {( , ) } ( , ) ( , ) ( , ) 2 边缘 分布 函数    离散型 连续型 —— 边缘分布列 —— 边缘概率密度    f x  f x y dy X ( ) ( , )    f y  f x y dx Y ( ) ( , ) X 与Y 的联合分布 F(x, y)  P{X x, Y  y} (X,Y)关于X 和Y 的边缘分布 F (x)  F(x,), X F ( y) F( , y) Y   关于X 的 关于Y 的 关于X 的 关于Y 的 { }, 1 i j i ij p   p  P X  x    { }, 1 i i j ij p   p  P Yy        y y Y j j F ( x) p     x x X i i F ( x) p       y Y F ( y) [ f (x,v)dx]dv       x FX (x) [ f (u, y)dy]du

复习 两个常见的二维分布 1.均匀分布 后，x时=G; G是平面上的有界区域 0, 其它， S为其面积. 2.正态分布 (X,)~N(41,,2,o,p). )=2πGg2,1-2e2Fp阿ay2p)a2H(1 -0<X<十+0，-0<y<+0 二维均匀分布的两个边缘密度未必是均匀分布 二维正态分布的两个边缘密度仍是正态分布

复习 两个常见的二维分布 1. 均匀分布       0 , , ; , ( , ) 1 ( , ) 其它 x y G f x y S G是平面上的有界区域 S为其面积. 2. 正态分布 (X,Y)～N(  ,  , , ,  ). 2 2 2 2 1 1 二维均匀分布的两个边缘密度未必是均匀分布 二维正态分布的两个边缘密度仍是正态分布 x,  y [( ) 2 ( )( ) ( ) ] 2 (1 ) 1 2 2 2 2 2 1 1 2 1 1 2                   x x y y e2 2 2 1 1 ( , )      1 f x y

我们与一维情形相对照，采用类比和转化的手段 介绍了二维随机变量的联合分布、边缘分布. 联合分布和边缘分布的关系： 由联合分布可以确定边缘分布； 但由边缘分布一般不能确定联合分布. 二维随机变量的两个随机变量之间的关系？ 条件概率 独立性

联合分布和边缘分布的关系: 我们与一维情形相对照，采用类比和转化的手段, 介绍了二维随机变量的联合分布、边缘分布. 由联合分布可以确定边缘分布; 但由边缘分布一般不能确定联合分布. 二维随机变量的两个随机变量之间的关系？ 条件概率 独立性

§3.3二维随机变量的条件分布 在第一章中，我们介绍了条件概率的概念 在事件B发生的条件下事件A发生的条件概率 P(AB 推广到 P(A B) P(B 随机变量 设有两个随机变量X,Y,在给定Y取某个 或某些值的条件下，求X的概率分布. 这个分布就 身高Y 例如，考虑某大学的全体学生， 是条件分布 从其中随机抽取一个学生，分别以X和Y表示其 体重和身高.则X和Y都是随机变量，它们都有一 定的概率分布. 体重X

在事件B 发生的条件下事件A 发生的条件概率 设有两个随机变量X, Y ， 这个分布就 是条件分布 随机变量 推广到 ( ) ( ) ( | ) P B P AB P A B  例如,考虑某大学的全体学生, 则X 和Y 都是随机变量,它们都有一 定的概率分布. 在第一章中，我们介绍了条件概率的概念 体重X 身高Y 从其中随机抽取一个学生，分别以X 和Y 表示其 体重和身高. 在给定 Y 取某个 或某些值的条件下,求 X 的概率分布. §3.3 二维随机变量的条件分布

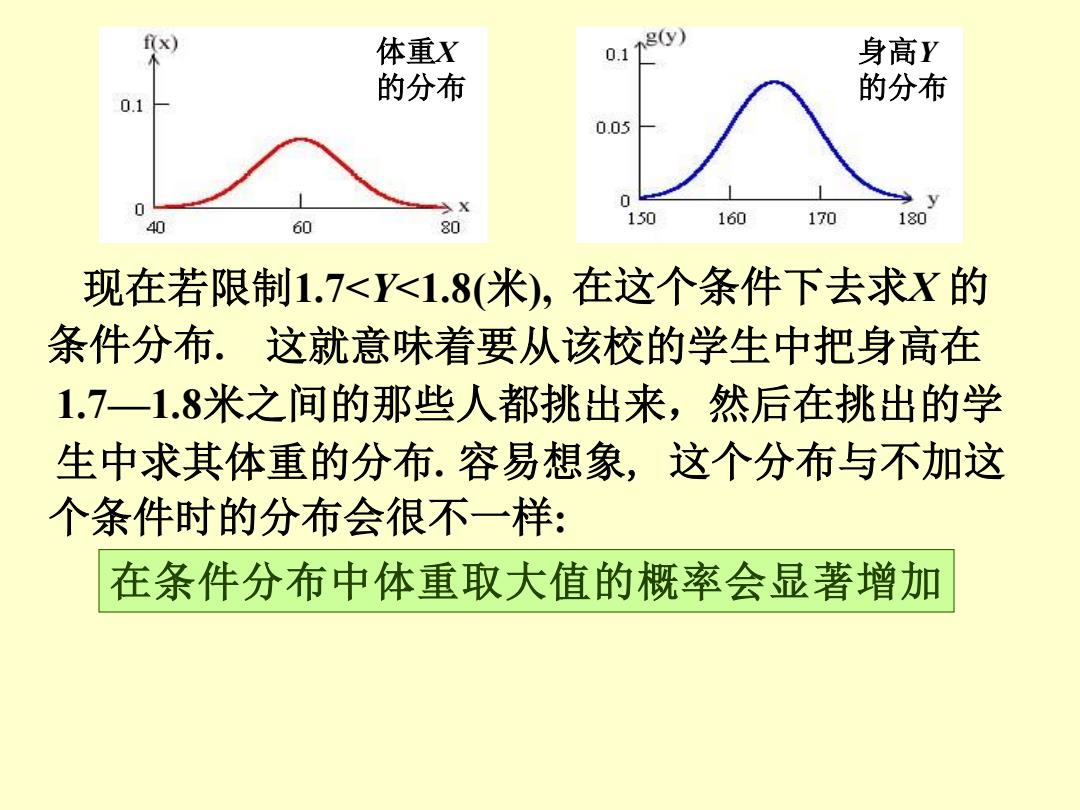
f(x) 体重X g(y) 0.1 身高Y 的分布 的分布 0.1 0.05 0 40 60 80 150 160 170 180 现在若限制1.7<Y<1.8(米)，在这个条件下去求X的 条件分布.这就意味着要从该校的学生中把身高在 1.7一1.8米之间的那些人都挑出来，然后在挑出的学 生中求其体重的分布.容易想象，这个分布与不加这 个条件时的分布会很不一样： 在条件分布中体重取大值的概率会显著增加

在这个条件下去求X 的 条件分布. 容易想象, 这个分布与不加这 个条件时的分布会很不一样: 在条件分布中体重取大值的概率会显著增加 现在若限制1.7<Y<1.8(米), 这就意味着要从该校的学生中把身高在 1.7—1.8米之间的那些人都挑出来，然后在挑出的学 生中求其体重的分布. 体重X 的分布 身高Y 的分布