第四章随机变量的数字特征 在前面的课程中,我们讨论了随机变量及其分布,如果知道了 随机变量X的概率分布, P(x) f(x) 那么X的全部概率特征 也就知道了
如果知道了 随机变量X 的概率分布, 那么X 的全部概率特征 也就知道了. x p(x) o f (x) o x 第四章 随机变量的数字特征 在前面的课程中,我们讨论了随机变量及其分布

但在实际问题中,概率分布一般是较难确定的.而且在一些实 际应用中,人们并不需要知道随机变量的一切概率性质,只要知道 它的某些数字特征就够了. 评定一批灯泡的质量,主要应看这批灯泡的平均寿命和灯 泡寿命相对于平均寿命的偏差,平均寿命越长,灯泡的质量 就越好,灯泡寿命相对于平均寿命的偏差越小,灯泡的质量就越稳定 因此,在对随机变量的研究中,确定某些数字特征是重要的. 在这些数字特征中,最常用的是抽象自平均值的期望和抽象自与平 均值的偏差程度的方差. 我们先介绍随机变量的数学期望
而且在一些实 际应用中,人们并不需要知道随机变量的一切概率性质,只要知道 它的某些数字特征就够了. 和抽象自与平 均值的偏差程度的方差. 平均寿命越长,灯泡的质量 就越好, 主要应看这批灯泡的平均寿命和灯 泡寿命相对于平均寿命的偏差, 但在实际问题中,概率分布一般是较难确定的. 因此,在对随机变量的研究中,确定某些数字特征是重要的 . 在这些数字特征中,最常用的是抽象自平均值的期望 我们先介绍随机变量的数学期望. 评定一批灯泡的质量, 灯泡寿命相对于平均寿命的偏差越小,灯泡的质量就越稳定
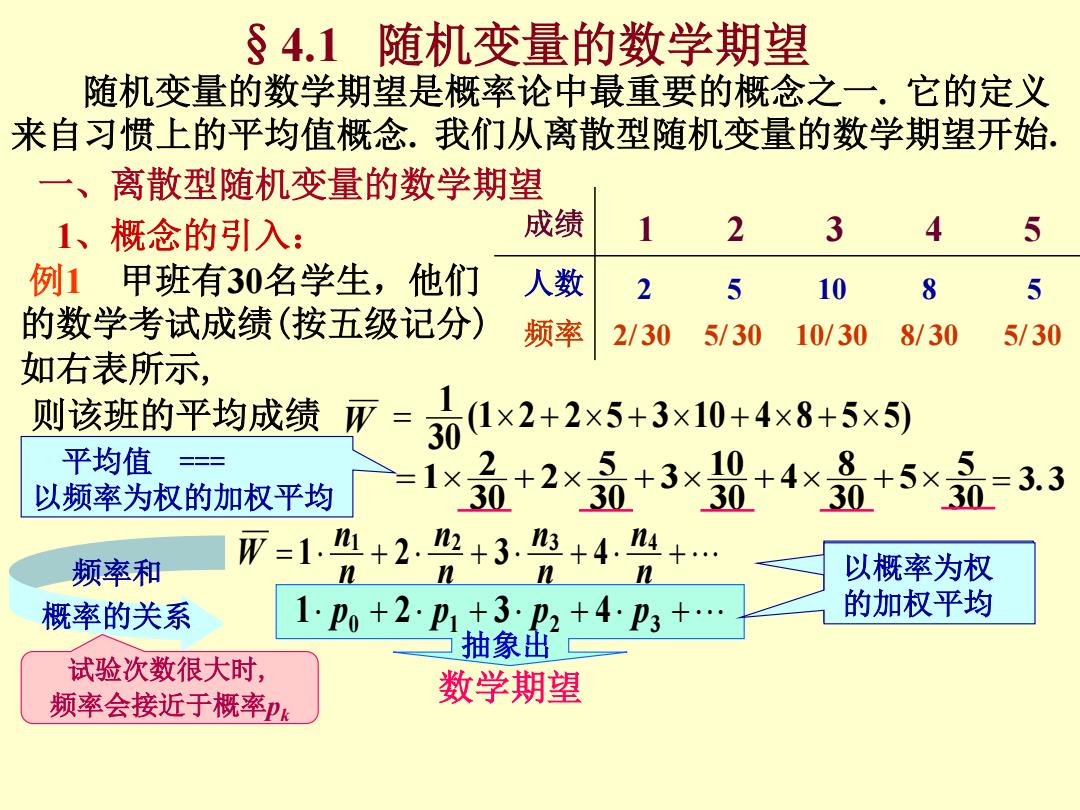
§4.1随机变量的数学期望 随机变量的数学期望是概率论中最重要的概念之一.它的定义 来自习惯上的平均值概念.我们从离散型随机变量的数学期望开始. 一、离散型随机变量的数学期望 1、概念的引入: 成绩 2 3 4 5 例1甲班有30名学生,他们 人数 2 5 10 8 5 的数学考试成绩(按五级记分) 频率 2/30 5/30 10/30 8/30 5/30 如右表所示, 则该班的平均成绩 币 301x2+2x5+3x10+4×8+5×5 平均值 二二二 以频率为权的加权平均 i品+2×+3×+4×最+5 30 =3.3 币=1.+2.2+3.+4.4+… 频率和 以概率为权 概率的关系 1p+2p1+32+4p3+… 的加权平均 抽象出 试验次数很大时, 频率会接近于概率pk 数学期望
抽象出 随机变量的数学期望是概率论中最重要的概念之一. 它的定义 来自习惯上的平均值概念. 我们从离散型随机变量的数学期望开始. §4.1 随机变量的数学期望 一、离散型随机变量的数学期望 1、概念的引入: 例1 甲班有30名学生,他们 的数学考试成绩(按五级记分) 如右表所示, 则该班的平均成绩 (1 2 2 5 3 10 4 8 5 5) 30 1 W 成绩 1 2 3 4 5 人数 频率 2 5 10 8 5 2/ 30 5/ 30 10/ 30 8/ 30 5/ 30 30 5 5 30 8 4 30 10 3 30 5 2 30 2 1 3.3 平均值 === 以频率为权的加权平均 改以频率为权 的加权平均 n n n n n n n n W 1 2 3 4 1 2 3 4 频率和 概率的关系 1 p0 2 p1 3 p2 4 p3 以概率为权 数学期望 试验次数很大时, 频率会接近于概率pk

定义1(P.98定义4,1)设离散型随机变量X的分布列是P(X=x)=,1,2,… 如果∑|x;P:收敛,则称∑xkPk为X的数学期望(期望)或均值, 1 k=1 记为EX.即EX=之xkPk. E(X,Y)=>xiyPi. k=1 =1 离散型随机变量的数学期望是一个绝对收敛级数的和 它是随机变量所有取值的以概率为权的加权平均 例2从学校乘汽车到火车站的途中有3个交通岗, 设在各交通岗遇到红灯的事件是相互独立的,其概率为2/5, 试求途中遇到红灯次数的数学期望. 解设X为遇到的红灯数,则X的分布列为 P(X=k)=C(2)()3(k=01,2,3, X 0 1 3 Pk 7/125 54/12536/125 8/125 Ex=0×s+I×话+2× +3 8-= 12 6-5
离散型随机变量的数学期望是一个绝对收敛级数的和 1 | | i 如果 x i pi 收敛, 定义1(P.98 定义4.1)设离散型随机变量X的分布列是P(X=xi)=pi , i=1,2,„ k1 则称 xk pk 为X 的数学期望(期望) 记为 EX . 125 8 3 125 36 2 125 54 1 125 7 EX 0 设在各交通岗遇到红灯的事件是相互独立的, 或均值, 例2 从学校乘汽车到火车站的途中有3个交通岗, 试求途中遇到红灯次数的数学期望. 解 设X为遇到的红灯数, 则X 的分布列为 ) ( 0,1,2,3), 5 3 ) ( 5 2 ( ) ( 3 3 P X k C k k k k X 0 1 2 3 pk 7/125 54/125 36/125 8/125 . ( , ) 1 1 i j j ij . E X Y xi y p 1 k 即 EX xk pk 其概率为2/5, 5 . 6 它是随机变量所有取值的以概率为权的加权平均

二、连续型随机变量的数学期望 设X是连续型随机变量,其密度为f(x),在数轴上任取很密的分 点x<x,<3<…,则X落在小区间[xk,X+△x)内的概率是 fx)fxAx: f(x) 小面积近似为 由于xk与x+△x很接近,所以区间 f(Xk)△xk [xk,x+△xk)中的值可以用x来近似代替 因此X≈取值xk概率为f(ck)△xk的离散型随机变量, X XI X2 Xk Pkf(c)△x fc2)△x2 f(Kk)△xk xf(x)dx 的积分和式 它的数学期望是im∑xkf(xk)△rk=xf() 20k 这启发我们引进如下连续型随机变量的数学期望定义: 定义2(P.100定义4,2)设X是连续型随机变量,其密度函数为f(x), 若Ixf(x)k收敛,则称EX=xf(x)为X的数学期望, 简称期望或均值 E(X,Y)=xyf(x,y)dxdy 连续型随机变量的数学期望是一个绝对收敛的积分
lim xf (x)dx 0 在数轴上任取很密的分 点 x1<x2<x3< „, 则X 落在小区间[xk , xk+xk)内的概率是 设X 是连续型随机变量,其密度为 f (x), k k k x x x f x dx ( ) ( ) . xk xk f 由于 xk 与 xk+xk 很接近, 所以区间 [xk , xk+xk )中的值可以用 xk 来近似代替. 因此 X ≈ 取值 xk、概率为 f (xk )xk 的离散型随机变量, 它的数学期望是 k k xk xk x f ( ) 的积分和式 x f (x)dx 这启发我们引进如下连续型随机变量的数学期望定义: 定义2(P.100 定义4.2) 设 X是连续型随机变量, 其密度函数为 f (x), 若 收敛, | x | f (x)dx 则称 为X 的数学期望, EX x f (x)dx 连续型随机变量的数学期望是一个绝对收敛的积分 小面积近似为 xk xk f ( ) 简称期望或均值. E(X,Y) xy f (x, y)dxdy X x1 x2 „ xk „ pk f (x1)x1 f (x2)x2 „ f (xk)xk „ f ( x) x 二、连续型随机变量的数学期望