《概率论与数理统计》课程教学资源（PPT课件）第6章 样本及抽样分布 第二次 抽样分布

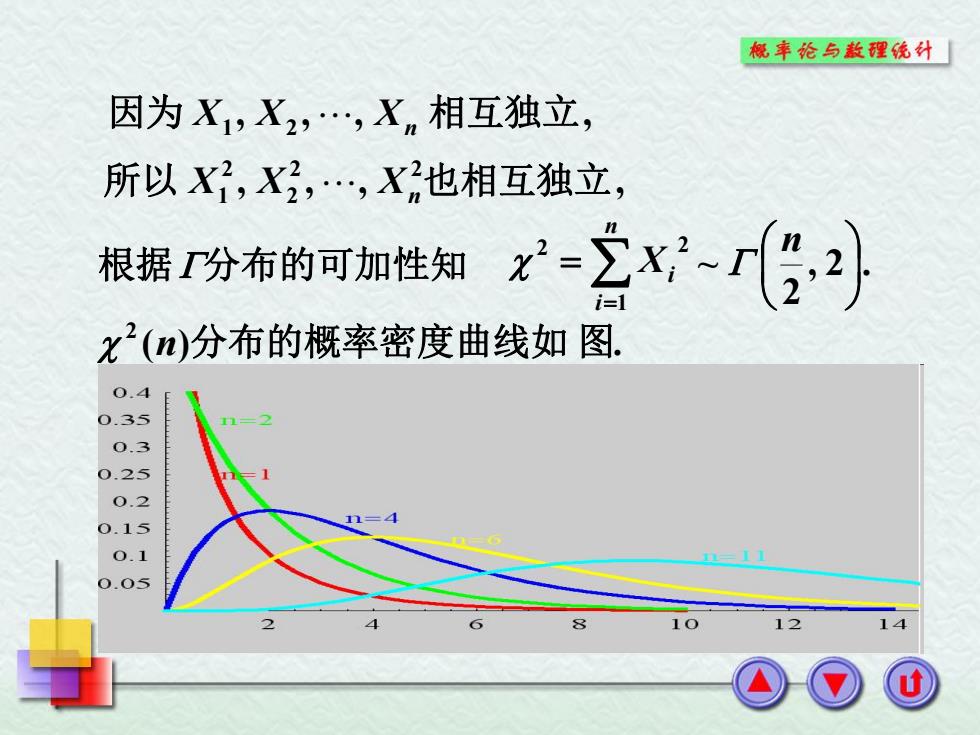
概奉论与散理统计 因为X1,X2,.,Xn相互独立， 所以X,X,X也相互独立， 根据r分布的可加性知x-立x”r经2习 x2(n)分布的概率密度曲线如图. 0.4 0.35 0.3 0.25 0.2 0.15 0.1 0.05 12

( ) .  2 n 分布的概率密度曲线如 图 , , , , 因为 X1 X2  Xn 相互独立 , , , , 2 2 2 2 所以 X1 X  Xn也相互独立 根据分布的可加性知   n i Xi 1 2 2  , 2 . 2 ~       n 

概率论与款理统外 x2分布的性质 性质1(x2分布的可加性) 设~x2(n),x2~x2(n2),并且1，x2独 立，则x+泾~x2(n1+n2): (此性质可以推广到多个随机变量的情形.) 设x~x2(n),并且x(i=1,2,.,m)相互 独立，则∑x~X(+++nm上

 2 分布的性质 性质1 , ~ ( ). ~ ( ), ~ ( ), , 1 2 2 2 2 2 1 2 2 2 2 1 2 2 1 2 2 2 1 n n n n            立 则 设 并且 独 ( )  2 分布的可加性 ( 此性质可以推广到多个随机变量的情形. ) , ~ ( ). ~ ( ), ( 1, 2, , ) 1 2 2 1 2 2 2 2 m m i i i i i n n n n i m             独立 则 设 并且 相互

概奉论与散理统计「 性质2(x分布的数学期望和方差) 若x2~x2(n,则E(x2)=n,D(x2)=2n. 证明因为X,~N(0,1),所以E(X2)=D(X)=1, D(X2)=E(X;)-[E(X2)=3-1=2=1,2,n. 故Ex)=2x2E(x)=nm 0x)=o2x}-2ox9=2m

性质2 ~ ( ), ( ) , ( ) 2 . 2 2 2 2 若   n 则 E   n D   n 证明 X ~ N(0, 1), 因为 i ( ) ( ) 1, 2 所以 E Xi  D Xi  2 4 2 2 ( ) ( ) [ ( )] D Xi  E Xi  E Xi  31  2i,  1, 2,, n.        n i E E Xi 1 2 2 故 ( )   n i E Xi 1 2 ( )  n,        n i D D Xi 1 2 2 ( )   n i D Xi 1 2 ( )  2n. ( )  2分布的数学期望和方差