
模拟滤波器原型的设计 为了检验此滤波器在2,和2s处的幅特性,可以用 连续系统频率特性计算函数freqs,它是freqz函 数在连续域的对等物。典型调用格式为: H=freqs(b,a,w) 用归一化参数时:H=freqs(b0,a0,w/OmegaC) 其中w为要取的频率向量,不允许取标量,故至 少要同时算两个频点。 若对频率范围不清楚,可以用另一种调用格式: [H,w]=freqs(b,a) 系统会自动选200个适当的频点进行计算。 21
21 模拟滤波器原型的设计 为了检验此滤波器在Ωp和Ωs处的幅特性,可以用 连续系统频率特性计算函数freqs,它是freqz函 数在连续域的对等物。典型调用格式为: H =freqs(b,a,w) 用归一化参数时:H =freqs(b0,a0,w/OmegaC) 其中w为要取的频率向量,不允许取标量,故至 少要同时算两个频点。 若对频率范围不清楚,可以用另一种调用格式: [H,w] =freqs(b,a) 系统会自动选200个适当的频点进行计算

模拟滤波器原型的设计 用以下语句可以检验设计结果: wx0=[5000,12000]*2*pi/37792;%两个频点 Hx=freqs(b0,a0,wx0)%计算该频率上的幅特性 dbHx=-20*logl0(abs(Hx)/max(abs(H))%分贝 运行程序得到dbHx=1.000032.1555 可见滤波器在OmegaP处的Rp=l分贝,在OmegaS 处的As=32分贝,满足了设计要求。 键入无左端变量的语句freqs(b,a),MATLAB会自 动给出系统的波德图。 22
22 模拟滤波器原型的设计 用以下语句可以检验设计结果: wx0=[5000, 12000]*2*pi/37792; % 两个频点 Hx=freqs(b0,a0,wx0) % 计算该频率上的幅特性 dbHx=-20*log10(abs(Hx)/max(abs(H))) % 分贝 运行程序得到 dbHx = 1.0000 32.1555 可见滤波器在OmegaP处的Rp=1分贝,在OmegaS 处的As=32分贝,满足了设计要求。 键入无左端变量的语句freqs(b,a),MATLAB会自 动给出系统的波德图
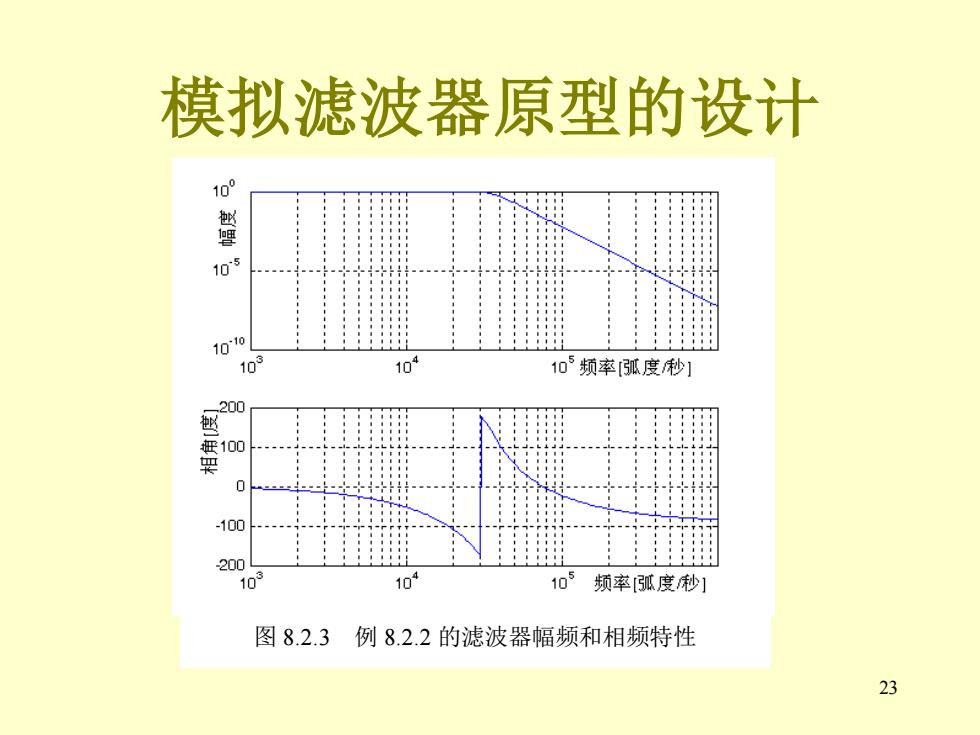
模拟滤波器原型的设计 10° 。 警 1010 103 104 105频率弧度秒] .200 100 -100 200 10 105 频率弧度秒] 图8.2.3 例8.2.2的滤波器幅频和相频特性 23
23 模拟滤波器原型的设计 图 8.2.3 例 8.2.2 的滤波器幅频和相频特性

切比雪夫I模拟原型的设计 切比雪夫滤波器具有波动性。它有两种类型:切 比雪夫I型在通带中具有等波动响应,而切比 雪夫Ⅱ型在阻带中具有等波动响应。切比雪夫 I型滤波器的平方幅度响应为: J2)=|Ha(U22 1+e2T(2/2c) 其中N为滤波器的阶数,ε为通带波动系数,它 与R,有关,TN(X)是N阶切比雪夫多项式 cos(N cos(x)) 0≤x≤1 TN(x)= cosh(cosh(x)). 1<x<0 24
24 切比雪夫I模拟原型的设计 切比雪夫滤波器具有波动性。它有两种类型:切 比雪夫Ⅰ型在通带中具有等波动响应,而切比 雪夫Ⅱ型在阻带中具有等波动响应。切比雪夫 Ⅰ型滤波器的平方幅度响应为: 其中N为滤波器的阶数,ε为通带波动系数,它 与Rp有关,TN (x)是N阶切比雪夫多项式 。 ( ) N c a T J H j + = = 2 2 2 1 1 ( ) ( ) = − − x x N x x T N x cosh(cosh ( )), 1 cos( cos ( )), 0 1 ( ) 1 1

切比雪夫I模拟原型的设计 切比雪夫滤波器的等波动响应是由多项式T(X)造 成的。它的主要性质是: (a)0<x<1时,Tx(x)在-1至1之间振荡: (b)0<x<∞时,Tx(X)单调增至∞。 为了确定一个因果的和稳定的系统,必须找出 J(2)的极点,它们应该是 1+827 的根。然后把左半平面的极点分配给Ha(s)。 25
25 切比雪夫I模拟原型的设计 切比雪夫滤波器的等波动响应是由多项式TN (x)造 成的。它的主要性质是: (a)0<x<1时,TN (x) 在 -1至1之间振荡; (b)0<x<∞时,TN (x)单调增至∞。 为了确定一个因果的和稳定的系统,必须找出 J(Ω2)的极点,它们应该是 的根。然后把左半平面的极点分配给Ha(s)。 1 0 2 2 = + c N j s T