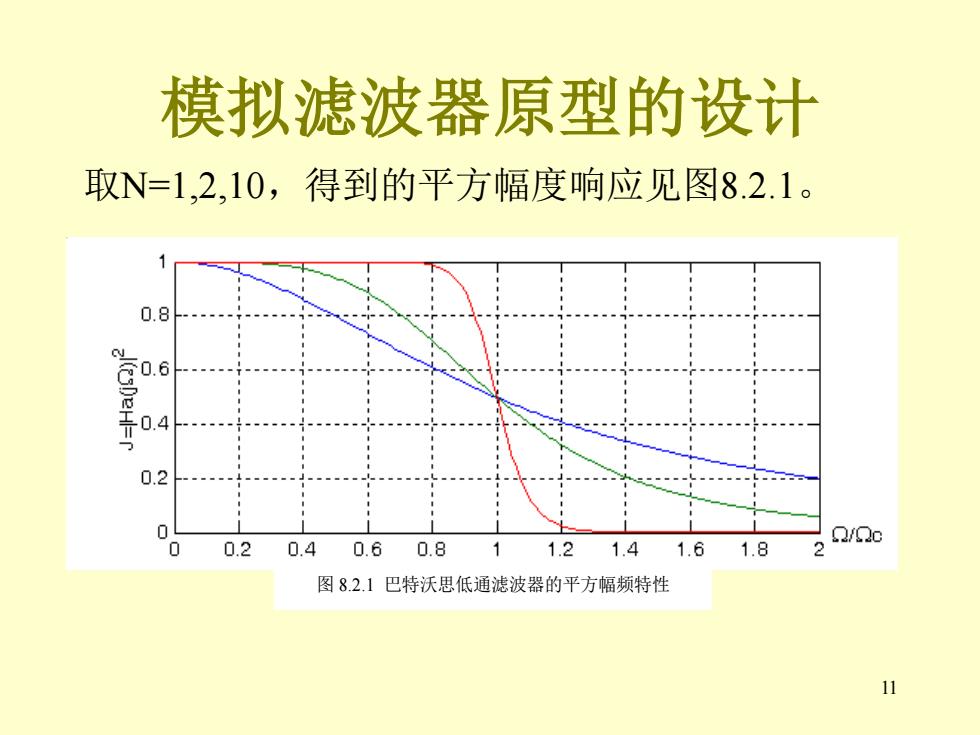
模拟滤波器原型的设计 取N=1,2,10,得到的平方幅度响应见图8.2.1。 0.8 S06 工 0.4 0.2 /e 0 0.2 0.40.6 0.8 1.2 1.41.61.8 2 图8.2.1巴特沃思低通滤波器的平方幅频特性 11
11 模拟滤波器原型的设计 取N=1,2,10,得到的平方幅度响应见图8.2.1。 图 8.2.1 巴特沃思低通滤波器的平方幅频特性

模拟滤波器原型的设计 为确定系统函数H(S),对J(2)进行零极点分解, H,A←s)=U22 s2+(02.) 特征方程 s2"+(2)2=0的根就是系统的极点, 且此滤波器没有零点。这2N个极点为 pk=(j2c)(-1)V2v=2.em(2k+W+I/2N k=0,1,…,2N-1 它们关于2对称,并绝不会落在虚轴上。 12
12 模拟滤波器原型的设计 为确定系统函数Ha (s),对J(Ω)进行零极点分解, 特征方程 的根就是系统的极点, 且此滤波器没有零点。 这2N个极点为 它们关于jΩ对称,并绝不会落在虚轴上。 ( ) ( ) 2 2 2 ( ) ( ) N c a a N N c j H s H s s j − = + ( ) 2 2 0 N N c s j + = 1/ 2 (2 1)/ 2 ( ) ( 1) , 0,1, ,2 1 N j k N N k c c p j e k N + + = − = = −
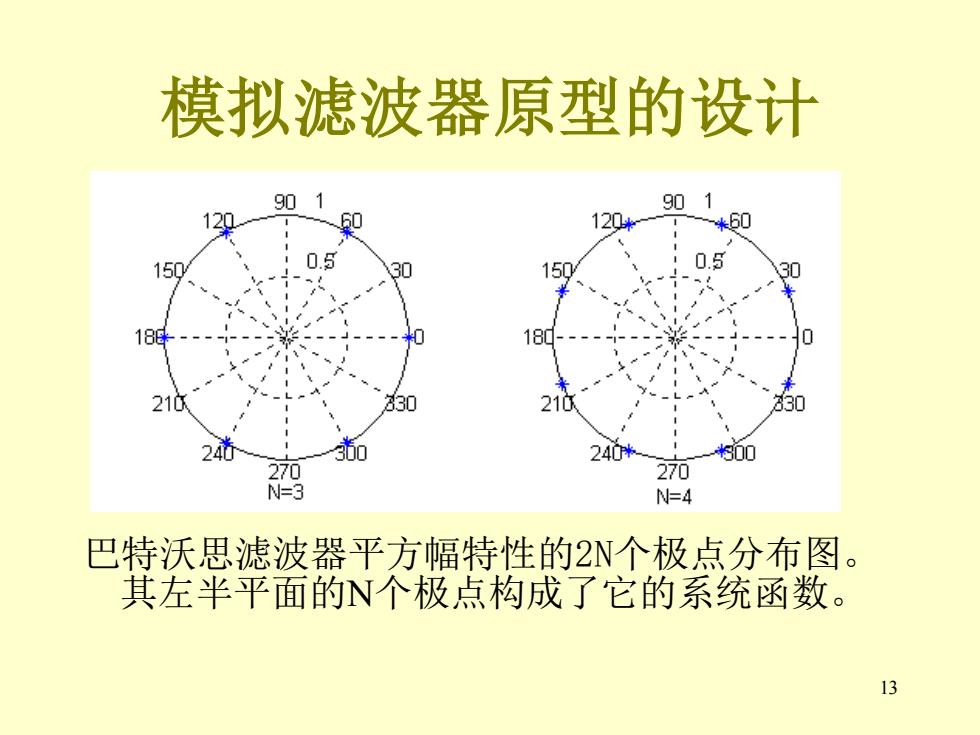
模拟滤波器原型的设计 90 90 129 120* 米60 150 05 0. 15 18沿 180---- 210 210 30 24 30 240* 00 270 270 N=3 N=4 巴特沃思滤波器平方幅特性的2N个极点分布图。 其左半平面的N个极点构成了它的系统函数。 13
13 模拟滤波器原型的设计 巴特沃思滤波器平方幅特性的2N个极点分布图。 其左半平面的N个极点构成了它的系统函数。 图 8.2.2 巴特沃思低通滤波器平方幅特性的极点分布

模拟滤波器原型的设计 例8.2.1给定Ha(22= 1+64Q8试确定模拟 滤波器的系统函数。 解:根据给定的条件:N=3,2。=0.5。 Ha(S)Ha(-S)的极点如上图左所示。取出左半平 面的三个极点,可写出系统函数 0.53 H(s)= (s+0.25-j0.433)(s+0.5)(s+0.25+j0.433) 0.125 (s+0.5)(s2+0.5s+0.25) 14
14 模拟滤波器原型的设计 例 8.2.1 给定 试确定模拟 滤波器的系统函数。 解:根据给定的条件:N=3,Ω c =0.5。 Ha(s)Ha(-s)的极点如上图左所示。取出左半平 面的三个极点,可写出系统函数 , 1 64 1 ( ) 6 2 + Ha j = 3 2 0.5 ( ) ( 0.25 0.433)( 0.5)( 0.25 0.433) 0.125 ( 0.5)( 0.5 0.25) H s a s j s s j s s s = + − + + + = + + +

模拟滤波器原型的设计 MATLAB提供了一个叫做outtap的函数,来设 计N阶归一化(即2=1)巴特沃思模拟原型滤 波器,其调用格式为 [z0,p0,ko]=buttap(N) 去归一化的零极点及增益为z=z02。、p-p0Qc及 k=k02N。 要求出系统函数分子分母的系数b和a,可用 b=poly(z);p=poly(p) 这使得高阶巴特沃斯滤波器的设计计算非常方便, 不必用查表的老办法。 15
15 模拟滤波器原型的设计 MATLAB提供了一个叫做buttap的函数,来设 计N阶归一化(即Ωc=1)巴特沃思模拟原型滤 波器,其调用格式为 [z0,p0,k0]=buttap(N)。 去归一化的零极点及增益为z=z0Ωc、p=p0Ωc 及 k=k0Ωc N 。 要求出系统函数分子分母的系数b和a,可用 b=poly(z); p=poly(p) 这使得高阶巴特沃斯滤波器的设计计算非常方便, 不必用查表的老办法