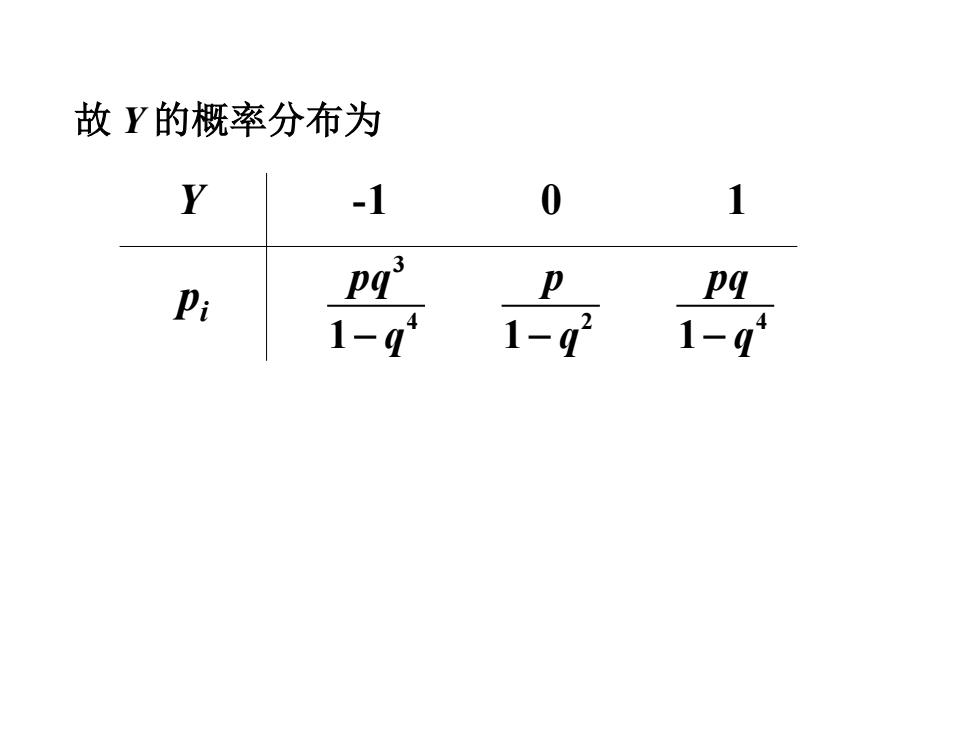
故Y的概率分布为 -1 0 Pi pqi 1-q
故 Y 的概率分布为 Y pi -1 0 1 3 424 111 pq p pq −−− qqq

二、连续型随机变量函数的分布 已知随机变量X的密度函数fx)(或分布函数) 求Y=(X)的密度函数或分布函数 方法: (1) 从分布函数出发,求出的分布函数 (2) 通过求导得密度函数 (1) 先求Y=g(X)的分布函数 F(y)=P{Y≤y以=P{g(X)≤y=∫fx(x) g(x)≤y (2)利用Y=g(X)的分布函数与密度函数之间的 关系求Y=g(X)的密度函数f(y)=FY(y): 10
已知随机变量 X 的密度函数 f (x) (或分布函数) 求 Y = g( X ) 的密度函数或分布函数 方法: (1) 从分布函数出发,求出Y的分布函数 (2) 通过求导得密度函数 二、连续型随机变量函数的分布 ⑴ 先求Y gX = ( )的分布函数 ( ) ( ) Y gX Y gX = = ⑵ 利用 的分布函数与密度函数之间的 关系求 的密度函数 F y PY y Y ( ) = ≤ { }= ≤ PgX y { ( ) } ( ) ( ) X gx y f x dx ≤ = ∫ ( ) ( ). Y Y f y Fy = ′ 10

例 设随机变量X具有概率密度: f=0, 2x,0<x<1, 其它 试求=X-4的概率密度. 解:先求Y=X-4的分布函数Fy): E,(y)=P{Y≤y} =P{X-4≤y}=P{X≤y+4} 11
2 , 0 1, ( ) 0, . X x x f x < < = 其它 设随机变量 X 具有概率密度: 试求 Y=X-4 的概率密度. 解: 先求 Y =X-4 的分布函数 FY(y): () { } F y PY y Y = ≤ 例 = −≤ = ≤+ PX y PX y { 4 } { 4} 11