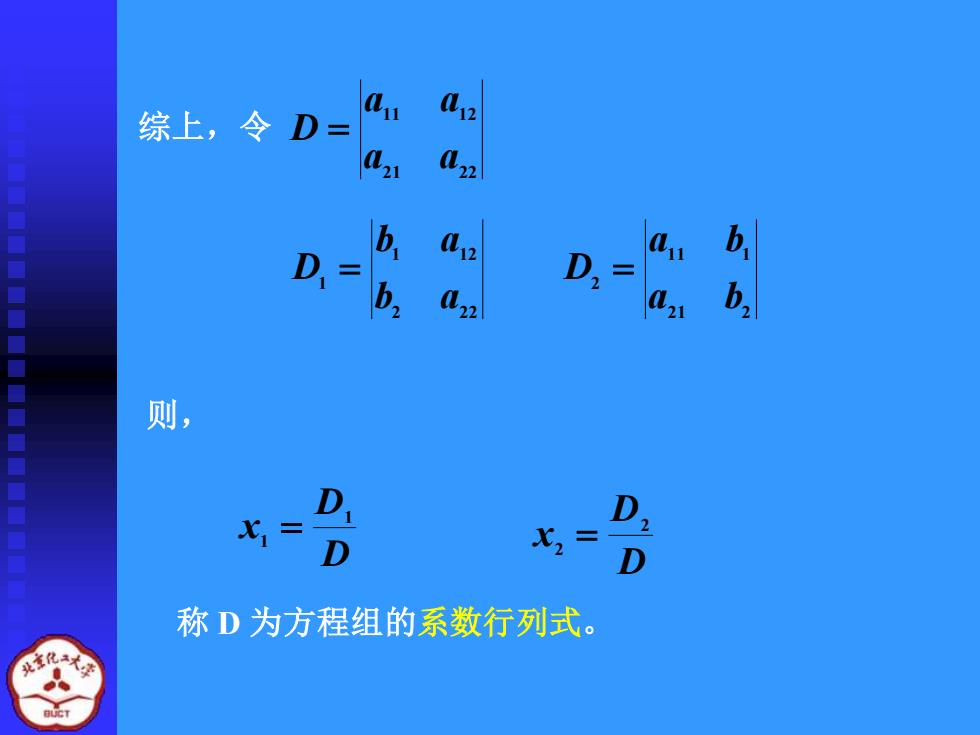
综上,令D 02 02 022 b D 么 D b 则, D D D 称D为方程组的系数行列式
综上,令 21 22 11 12 a a a a D = 2 22 1 12 1 b a b a D = 21 2 11 1 2 a b a b D = 则, D D x 1 1 = D D x 2 2 = 称 D 为方程组的系数行列式

例1: 解方程组 3x1-2x=12 2x+x2=1 3-2 解: 因为 D= 2 =3-(-4)=7≠0 12 -2 D、 =12-(-2)=14 D2= =3-24=-21 所以飞 D =2, -21 =-3
例1: 解方程组 + = − = 2 1 3 2 12 1 2 1 2 x x x x 解: 因为 2 1 3 − 2 D = = 3 − (−4) = 7 0 12 ( 2) 14 1 1 12 2 1 = − − = − D = 3 24 21 2 1 3 12 D2 = = − = − 所以 2 , 7 1 14 1 = = = D D x 3 7 2 21 2 = − − = = D D x

2,三阶行列式 类似地,为讨论三元线性方程组 01'1+42X2+013火3=b L21+022X2+L23X3=b 01X1+032X2+033少3=b, 记 0 m 03 D 0 022 03 01022L33+012L23031+L1302L32 031 032 U38 -L1302z031-1221L33-010230z 称为三阶行列式 其中,数0(i=1,2,3j=1,2,3)称为元素 i为行标,j为列标
2. 三阶行列式 类似地,为讨论三元线性方程组 + + = + + = + + = 31 1 32 2 33 3 3 21 1 22 2 23 3 2 11 1 12 2 13 3 1 a x a x a x b a x a x a x b a x a x a x b 记 31 32 33 21 22 23 11 12 13 a a a a a a a a a D = = 13 22 31 12 21 33 11 23 32 11 22 33 12 23 31 13 21 32 a a a a a a a a a a a a a a a a a a − − − + + 称为三阶行列式 其中 ,数 a (i = 1,2,3; j = 1,2,3) ij 称为元素 i 为行标, j 为列标

注: (1)三阶行列式算出来也是一个数。 (2)运算方法:对角线法则 例: 4 8 3 =2×(-4)×3+0×(-1)×(-1)+1×1×8 -1×(-4)×(仁-1)-0×1×3-2×(-1)×8 =-24+8-4+16=-4
注: (1) 三阶行列式算出来也是一个数。 (2) 运算方法:对角线法则 例: 1 8 3 1 4 1 2 0 1 − − − 24 8 4 16 4 1 ( 4) ( 1) 0 1 3 2 ( 1) 8 2 ( 4) 3 0 ( 1) ( 1) 1 1 8 = − + − + = − − − − − − − = − + − − +