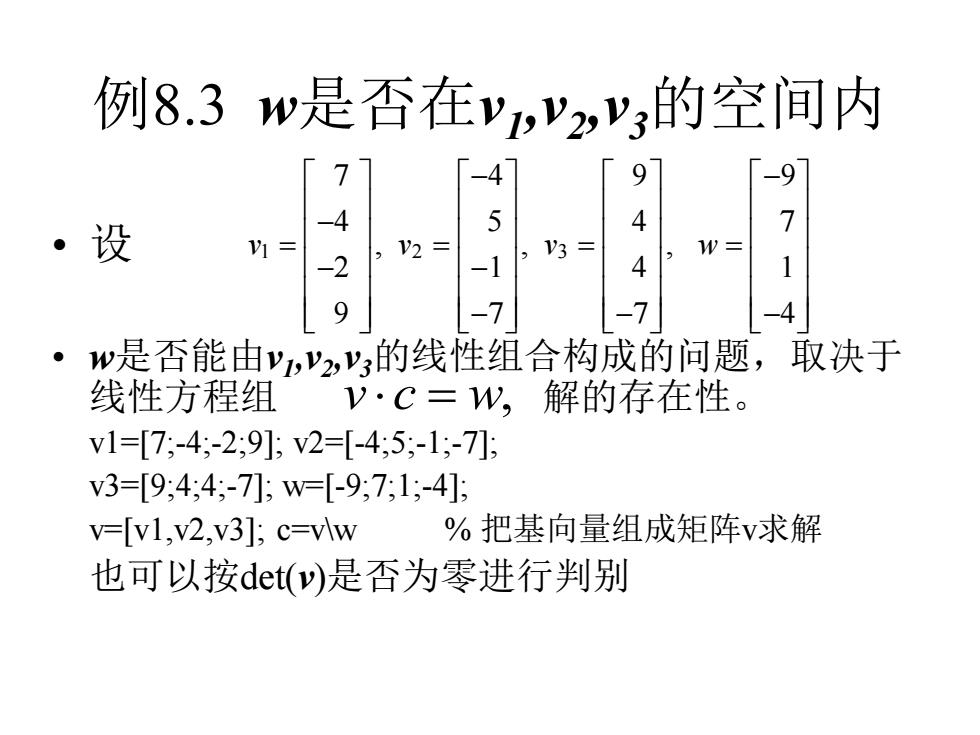
例8.3w是否在ypy2,y3的空间内 4 -9 7 ·设 1= 2 W= -4 w是否能由yy2,y3的线性组合构成的问题,取决于 线性方程组 V·C=W,解的存在性。 v1=[7;-4;-2;9];2=[-45;-1,-7]; 3=[9;4;4;-7];w=[-9,7;1;-4] v=[v1,2,v3];c=Vw %把基向量组成矩阵v求解 也可以按det()是否为零进行判别
例8.3 w是否在v1 ,v2 ,v3的空间内 • 设 • w是否能由v1 ,v2 ,v3的线性组合构成的问题,取决于 线性方程组 解的存在性。 v1=[7;-4;-2;9]; v2=[-4;5;-1;-7]; v3=[9;4;4;-7]; w=[-9;7;1;-4]; v=[v1,v2,v3]; c=v\w % 把基向量组成矩阵v求解 也可以按det(v)是否为零进行判别 1 2 3 7 4 9 9 4 5 4 7 , , , 2 1 4 1 9 7 7 4 v v v w − − − = = = = − − − − − v c w =

8.3向量的内积和正交性 ·在三维空间中,x和y两个向量的内积定义 为x,y]=xy,y23。m维情况可以写成 [k月=)=n+%++x-2xy i=1 ·这是一个标量。向量x与自己求内积: m xx=x+x2x2+…+Xmxm=∑x 2 i=l 0 得到的是其各分量的平方和,其平方根就 等于向量的长度(或模、或范数norm)
8.3 向量的内积和正交性 • 在三维空间中,x和y两个向量的内积定义 为[x,y]=x1 y1+x2 y2+x3 y3。m维情况可以写成 • 这是一个标量。向量x与自己求内积: • 得到的是其各分量的平方和,其平方根就 等于向量的长度(或模、或范数norm)。 1 1 2 2 1 m T m m i i i x y x y x y x y x y = x, y = = + + + = 2 1 1 2 2 1 m m m i i x x x x x x x = = + + + = T x x
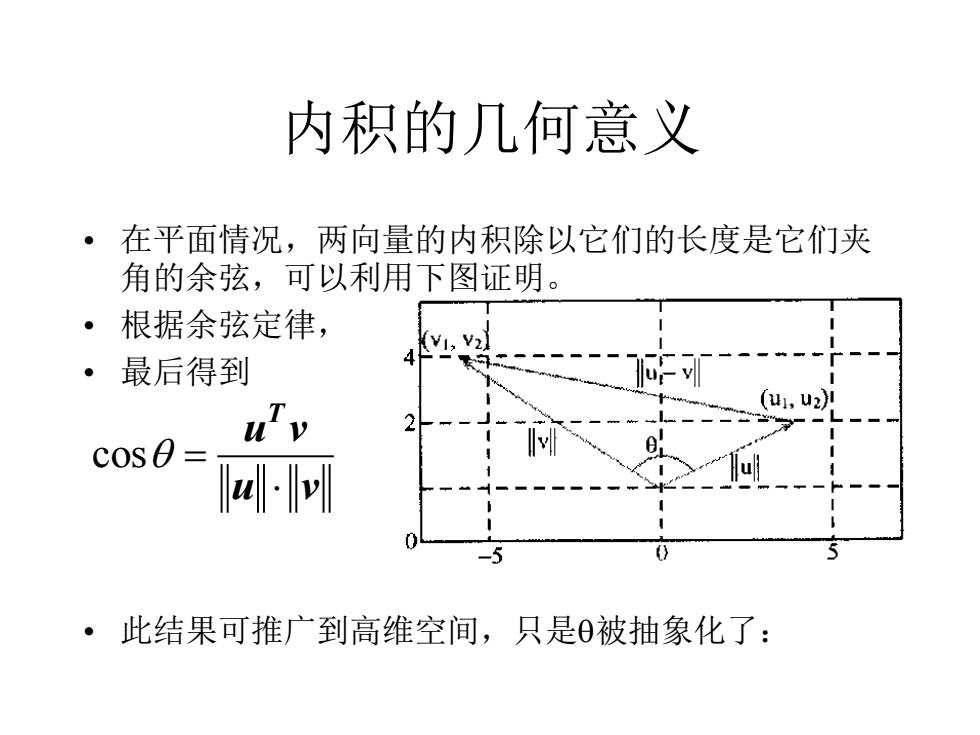
内积的几何意义 ·在平面情况,两向量的内积除以它们的长度是它们夹 角的余弦,可以利用下图证明。 。 根据余弦定律, 4,2 ·最后得到 1,u2 u"v 2 c0S0= l4- ·此结果可推广到高维空间,只是0被抽象化了:
内积的几何意义 • 在平面情况,两向量的内积除以它们的长度是它们夹 角的余弦,可以利用下图证明。 • 根据余弦定律, • 最后得到 • 此结果可推广到高维空间,只是被抽象化了: cos = T u v u v

例8.4基向量长度规一化和夹 角 。个 例8.4求例8.3中的单位基向量v10,v20,v30,并 分别求它们之间的夹角。 ·解:解题的程序为ag822: v10=v1/norm(v1), v20=v2/norm(v2), v30=v3/norm(v1), thetal2=acos((v1'*v2)/(norm(v1)*norm(v2))) thetal3=acos((v1'*v3)/(norm(v1)*norm(v3))) theta23=acos((v3'*v2)/(norm(v3)*norm(v2)))
例8.4 基向量长度规一化和夹 角 • 例8.4 求例8.3中的单位基向量v10,v20,v30,并 分别求它们之间的夹角。 • 解:解题的程序为ag822: v10=v1/norm(v1), v20=v2/norm(v2), v30=v3/norm(v1), theta12=acos((v1'*v2)/(norm(v1)*norm(v2))) theta13=acos((v1'*v3)/(norm(v1)*norm(v3))) theta23=acos((v3'*v2)/(norm(v3)*norm(v2)) )