
n维向量的相关性 。 在进入三维以上的空间时,已经没有可 与面积、体积直接相当的概念可用了, 所以采用了秩的概念。如果A的行列式为 零,也就是它的秩r小于n时,说明这n个 向量是线性相关的。 秩的概念也概括了面积存在(=2)和体 积存在(=3)的意义,因此,它是更高 度的抽象
n维向量的相关性 • 在进入三维以上的空间时,已经没有可 与面积、体积直接相当的概念可用了, 所以采用了秩的概念。如果A的行列式为 零,也就是它的秩r小于n时,说明这n个 向量是线性相关的。 • 秩的概念也概括了面积存在(r=2)和体 积存在(r=3)的意义,因此,它是更高 度的抽象

8.2向量空间和基向量 ·若个向量是线性无关的,则它们的线性组合的 全体V就构成了r维空间Rr。如果它不是空集, 则V称为向量空间。生成V的r个线性无关的向 量v称为基向量或基(Basis)。 。} 当r=n时,给定的n个向量就是一组基。如果r<n, 那就要在n个向量中选出r个线性无关的向量 。 用秩的概念还无法判定哪些向量是线性无关的, 这时又要藉助于把矩阵简化为阶梯形式的方法
8.2 向量空间和基向量 • 若r个向量是线性无关的,则它们的线性组合的 全体V就构成了r维空间Rr 。如果它不是空集, 则V称为向量空间。生成V的r个线性无关的向 量v称为基向量或基(Basis)。 • 当r=n时,给定的n个向量就是一组基。如果rn, 那就要在n个向量中选出r个线性无关的向量。 用秩的概念还无法判定哪些向量是线性无关的, 这时又要藉助于把矩阵简化为阶梯形式的方法

例8.2求四个五维向量的子空间 4 -5 -4 ·这四个向量组成的矩 0 -3 0 阵如右,对它进行行 A= -2 1 0 -5 3 阶梯简化。程序为: -1 -1 A=[4,-5,-4,-1,0,-3,0,1;-2,1,2,0;-5,4,5,3;-1,4,1,-1] [UO,ip]=rref(A) 1 0 得到ip=1,2,4 0 0 其三个枢轴列对应的就是 U0= 0 0 三个线性无关的列向量。 0 0 0 0 0 0
例8.2 求四个五维向量的子空间 • 这四个向量组成的矩 阵如右,对它进行行 阶梯简化。程序为: A=[4,−5,−4,−1;0,−3,0,1;−2,1,2,0;−5,4,5,3;−1,4,1,−1] [U0,ip]=rref(A) 得到 ip=1,2,4 其三个枢轴列对应的就是 三个线性无关的列向量。 4 5 4 1 0 3 0 1 2 1 2 0 5 4 5 3 1 4 1 1 − − − − = − − − − A 1 0 1 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 − = U0

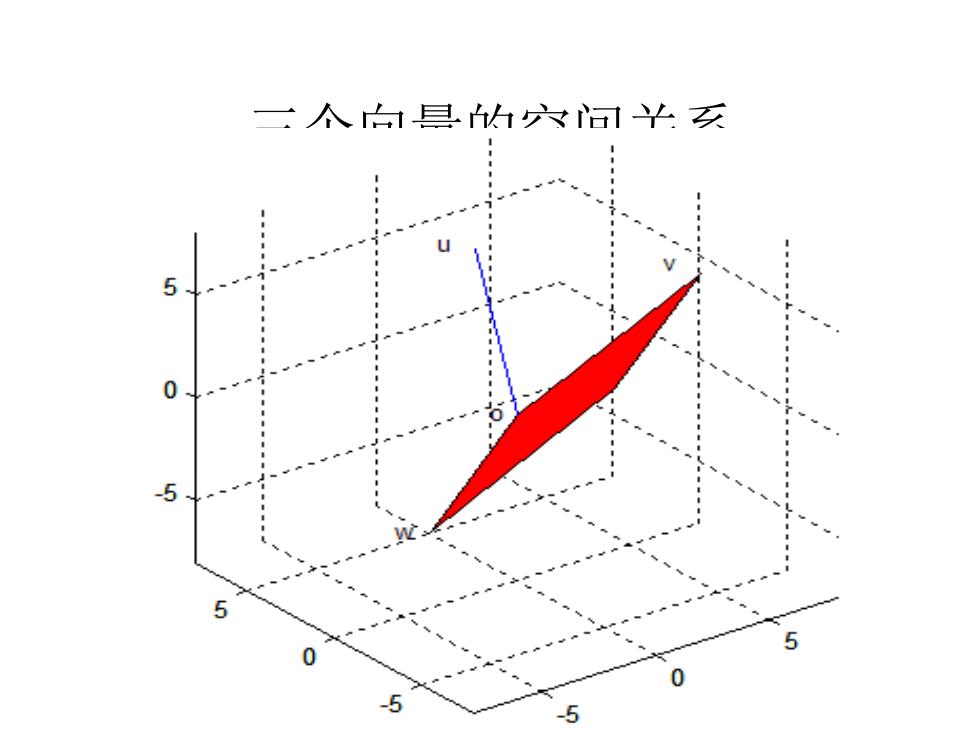
三个向量空间位置演示程序 三维空间中,为了观察三个向量的空间关系, ATLAST:手册还提供了一个演示程序 viewsubspaces(u,y,w),它用蓝色直线显示向量u, 同时用红色显示v和w所组张成的平行四边形平 面,画在同一张立体图上。例如: u=[-1;1;8]v=[5;-4,7],w=[-3,1;-5]; viewsubspaces(u,v,w),grid on 三个向量的起点都是x=y=z=0的原点。要看清其 几何意义,还是需要一定的空间想象力
三个向量空间位置演示程序 • 三维空间中,为了观察三个向量的空间关系, ATLAST手册还提供了一个演示程序 viewsubspaces(u,v,w),它用蓝色直线显示向量u, 同时用红色显示v和w所组张成的平行四边形平 面,画在同一张立体图上。例如: u=[-1;1;8];v=[5;-4;7];w=[-3;1;-5]; viewsubspaces(u,v,w),grid on 三个向量的起点都是x=y=z=0的原点。要看清其 几何意义,还是需要一定的空间想象力
二人县h六女.亥 5
三个向量的空间关系