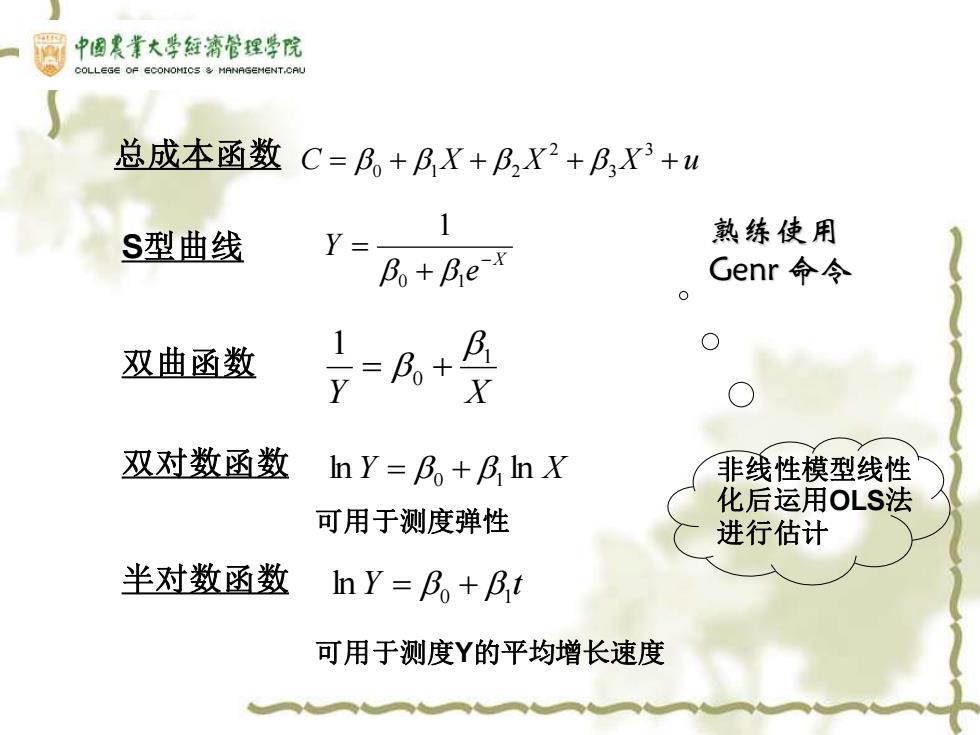
中国農常大学每濟管猩学院 COLLEGE OF ECONOMICS MANASEMENT.CAU 总成本函数C=B。+BX+B,X2+B,X3+u 1 S型曲线 Y= 熟练使用 Bo+Be-x Genr命令 双曲函数 =+是 X 双对数函数 hY=B。+B,hX 非线性模型线性 化后运用OLS法 可用于测度弹性 进行估计 半对数函数 hY=F。+Bt 可用于测度Y的平均增长速度
X e Y − + = 0 1 1 C = + X + X + X + u 3 3 2 0 1 2 Y X 1 0 1 = + 总成本函数 熟练使用 Genr 命令 S型曲线 非线性模型线性 化后运用OLS法 进行估计 双曲函数 双对数函数 ln Y = 0 + 1 ln X Y t 0 1 半对数函数 ln = + 可用于测度弹性 可用于测度Y的平均增长速度

中固发章大学每奢管理学院 COLLEGE OF ECONOMICS乡NT,CA 希克斯中性技术进步的C-D生产函数:技术进步前后,劳动的产出弹 性与资本的产出弹性同步增长,KL不随时间变化) Y=A(1)K(L (t) =(Ae")K(t)L(1) m表示技术进步率 取对数得: In Y=In 4+aIn K(t)+BIn L(t)+mt d(In Y)1 dy 1 dK 1 dl 微分得: X +B +m dt y dt K dt L dt a、B为资 产出增 资本增 劳动增 本弹性和劳 长率,记 长率,记 长率,记 动弹性 为y 为K 为L
希克斯中性技术进步的C-D生产函数:技术进步前后,劳动的产出弹 性与资本的产出弹性同步增长,K/L不随时间变化) ( ) ( ) ( ) ( ) ( ) ( ) 0 A e K t L t Y A t K t L t mt = = m 表示技术进步率 取对数得: ln Y = ln A + ln K(t) + ln L(t) + mt 0 微分得: m dt dL dt L dK dt K dY dt Y d Y = = + + (ln ) 1 1 1 产出增 长率,记 为y 资本增 长率,记 为K 劳动增 长率,记 为L α、β为资 本弹性和劳 动弹性

中国農業大学每奢管理学院 COLLEGE OF ECONOMICS MANASEMENT.CAL 技术进步率为: 1Y-a: 1 dk-B. 1 dl m= y dt K dt I dt 即: m=y-C·k-B·1←一索洛增长速度方程 技术进步贡献率: E1="mx100% 资本贡献率: ·k B=a ×100% E4+E,+Ex=1 y 劳动贡献率: E,=B-1×100%
技术进步率为: dt dL dt L dK dt K dY Y m 1 1 1 = − − 即: m = y − k − l 索洛增长速度方程 技术进步贡献率: = 100% y m EA 资本贡献率: 劳动贡献率: 100% = y k Ek 100% = y l El + + =1 EA EL EK

中国爱青大学每奢管理学院 COLLEGE OF ECONOMICS MANASEMENT.CAL 2、不可变换为线性的模型的估计,例: CES (Constant Elasticity of Substitution) 生产函数 Q=A(61KP+6,LP)Pe“ A:为规模参数(效率参数),反映技术发达程度; :分布参数,反映劳动密集程度。6,+δ,=1 p:替代参数 m:规模报酬参数
2、不可变换为线性的模型的估计,例: ◆ CES(Constant Elasticity of Substitution) 生产函数 u m Q A K L e − − − = ( + ) 1 2 A :为规模参数(效率参数), 反映技术发达程度; δ:分布参数, 反映劳动密集程度。δ1+δ2=1 ρ:替代参数. m: 规模报酬参数

中国農常大学每濟管猩学院 COLLEGE OF ECONOMICS MANASEMENT.CAL ◆泰勒级数展开法 (1) 非线性模型Y=f(X1,X2,XkB1,B2,Bp)+u (2)给定一组参数的初始值bo,b20,b0,将上式展开 r=x名.n+空器6-刻) 60b6,-bK6,-b+.+ i1 (3)取上式的前两项,得原函数近似线性表达式,用OLS 法进行估计,得出新的一组参数估计值b1,b21,b1,重复以上 过程,直到: (4) bt- b <6时,迭代结束
Y f X X X u = ( 1 , 2 ,., k; 1 , 2 ,., p ) + ◆泰勒级数展开法 b b b b u b b f b b b f Y f X X X b b b b b i i j j i j p j p i i p i b i i k p i j i − − ++ + − = + = = = ( ) ( )( ) 2 1 ( , , , ; , ,., ) ( ) ( ) 0 0 2 1 1 0 1 1 2 1 0 2 0 0 0 0 0 (3)取上式的前两项,得原函数近似线性表达式,用OLS 法进行估计,得出新的一组参数估计值 b11,b21,.,bp1 ,重复以上 过程,直到: (1)非线性模型 (2)给定一组参数的初始值 ,将上式展开 (4) ij ij ij b b +1 − b <δ 时,迭代结束。 10 20 0 , ,., b b bp