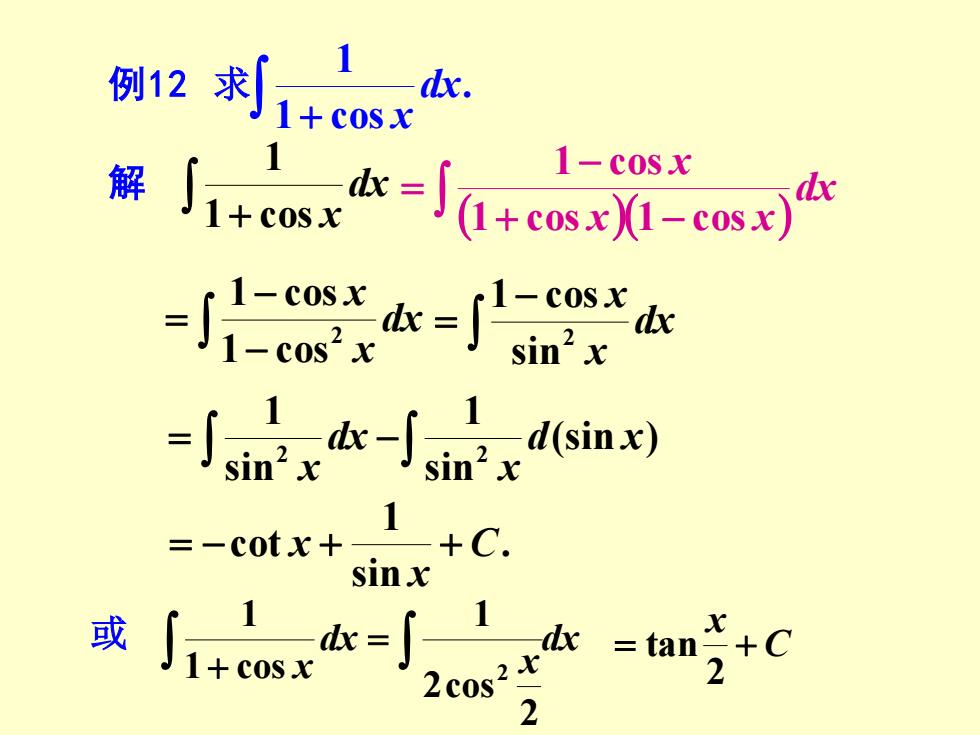
解∫1+cse=a+eseX-es可 1-cosx -=小 -ir-小sin') =-cotx+ -+C. sinx 2
例12 求 解 . 1 cos 1 + dx x + dx 1 cos x 1 ( )( ) + − − = dx x x x 1 cos 1 cos 1 cos − − = dx x x 2 1 cos 1 cos − = dx x x 2 sin 1 cos = − (sin ) sin 1 sin 1 2 2 d x x dx x . sin 1 cot C x = − x + + 或 dx x dx x = + 2 2cos 1 1 cos 1 2 C x = + 2 tan

例13求∫sin2 c.cos5xdx. 解「sin2xcos5xdk=∫sin2 .cosxd(sinx) sin2x.(1-sin2x)2d(sinx) (sin2x-2sin'x+sin x)d(sinx) 1 2 1 gsin'x-gsimn'sin'x+C. 3 说明当被积函数是三角函数相乘时,拆开奇 次项去凑微分
例13 求 解 sin cos . 2 5 x xdx x xdx 2 5 sin cos = sin cos (sin ) 2 4 x xd x = sin (1− sin ) (sin ) 2 2 2 x x d x = (sin − 2sin + sin ) (sin ) 2 4 6 x x x d x sin . 7 1 sin 5 2 sin 3 1 3 5 7 = x − x + x + C 说明 当被积函数是三角函数相乘时,拆开奇 次项去凑微分