
③凑微分法就在凑微分上,其基本思想就是对被积 表达式进行变形,主要考虑如何变化f(x)水 凑微分法的基本思路: 与基本积分公式相比较,将不同的部分 中间变量和积分变量— 变成相同 步骤:凑微分;换元求出积分;回代原变量 例1求sin2xdk. 解(一)jsin2x=sin2xd(2x) cos2.x+C;
③凑微分法就在凑微分上,其基本思想就是对被积 表达式进行变形,主要考虑如何变化 f (x)dx 凑微分法的基本思路: 与基本积分公式相比较,将不同的部分—— 中间变量和积分变量——变成相同 步骤:凑微分;换元求出积分;回代原变量 例1 求 sin2 . xdx 解(一) sin2xdx = sin2 (2 ) 2 1 xd x cos 2 ; 2 1 = − x + C
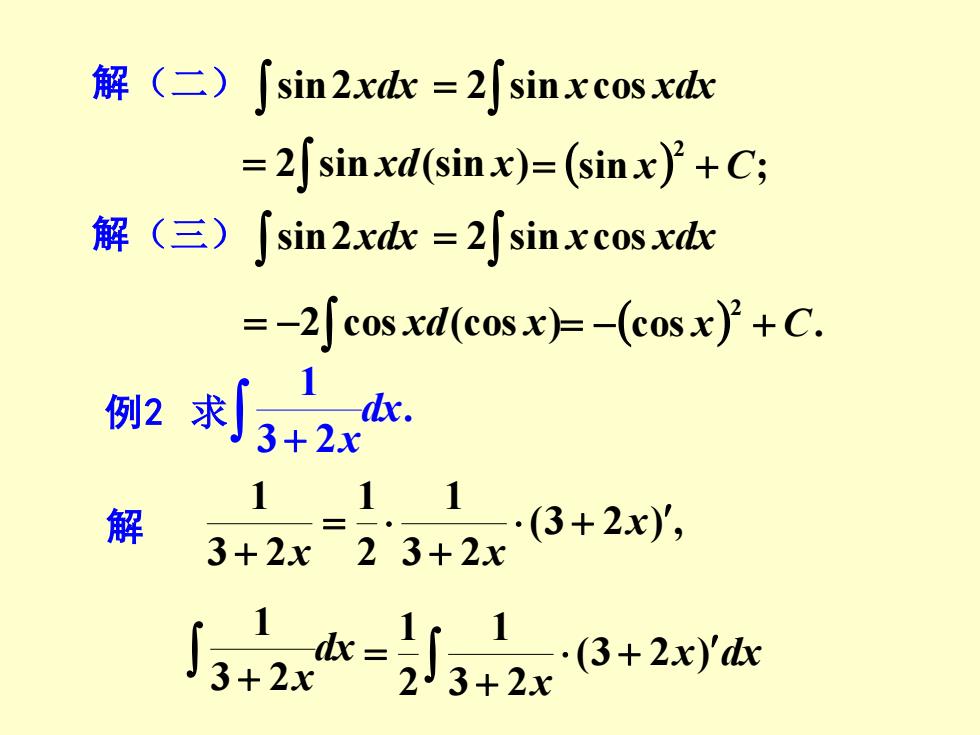
解(二)∫sin2xdk=2∫sinxcosxd =2Jsinxd(sinx)=(sinx)+C; 解(三)∫sin2xdk=2 sin xcosxo =-2fcosxd(cosx)=-(cosx)+C. 232盒 解 1=1.1-(3+2xy, 3+2x23+2x 3+2=32x0+2xy
解(二) sin2xdx = 2 sin xcos xdx = 2 sin xd(sin x) (sin ) ; 2 = x + C 解(三) sin2xdx = 2 sin xcos xdx = − 2 cos xd(cos x) (cos ) . 2 = − x + C 例2 求 . 3 2 1 dx x + 解 (3 2 ) , 3 2 1 2 1 3 2 1 + + = + x x x dx x 3 + 2 1 x dx x (3 2 ) 3 2 1 2 1 + + =
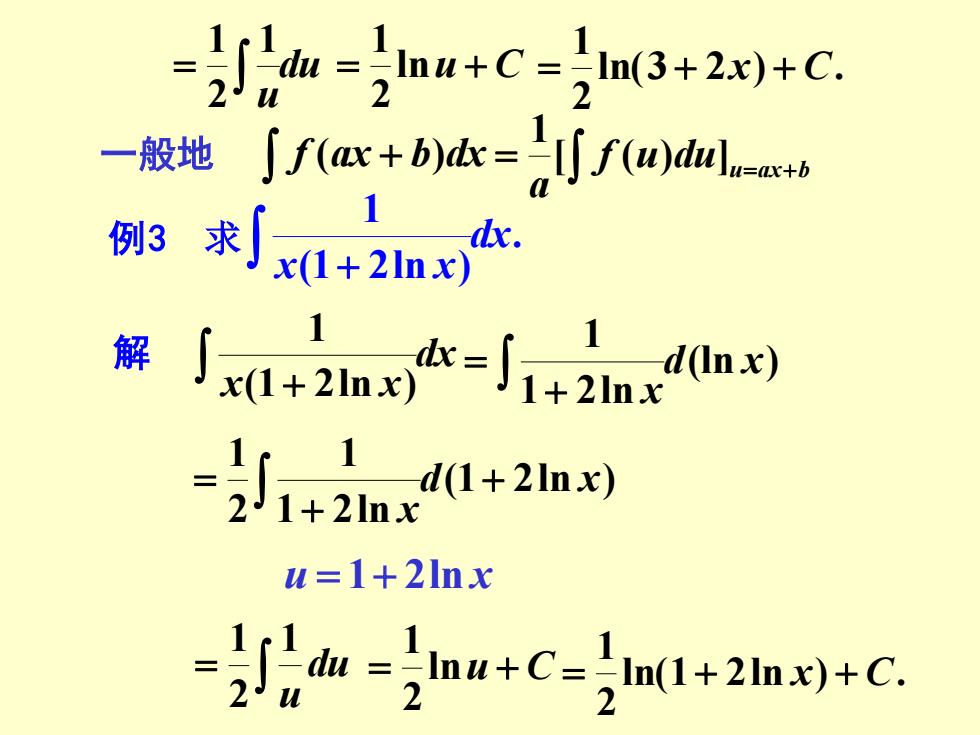
-打-ua+C=(3+2+C 一般地 ∫f(ax+b)c=f(w)du-+b 附求灯ka+2nc 解ju+2nr-j1+2nd0a 1+2n1+2n0 u=1+2Inx =打a=nu+c-n1+2na)+c
du u = 1 2 1 = lnu + C 2 1 ln(3 2 ) . 2 1 = + x + C f (ax + b)dx = u du u=ax+b f a [ ( ) ] 1 一般地 例3 求 . (1 2ln ) 1 dx x x + 解 dx x x (1+ 2ln ) 1 (ln ) 1 2ln 1 d x x + = (1 2ln ) 1 2ln 1 2 1 d x x + + = u = 1+ 2ln x = du u 1 2 1 = lnu + C 2 1 ln(1 2ln ) . 2 1 = + x + C

解 n4= d a+对a++刘 1 1 + +G+21++C 4*++
例4 求 . (1 ) 3 dx x x + 解 dx x x + 3 (1 ) dx x x + + − = 3 (1 ) 1 1 ] (1 ) (1 ) 1 (1 ) 1 [ 2 3 d x x x + + − + = 1 2 2 2(1 ) 1 1 1 C x C x + + + + + = − . 2(1 ) 1 1 1 2 C x x + + + + = −
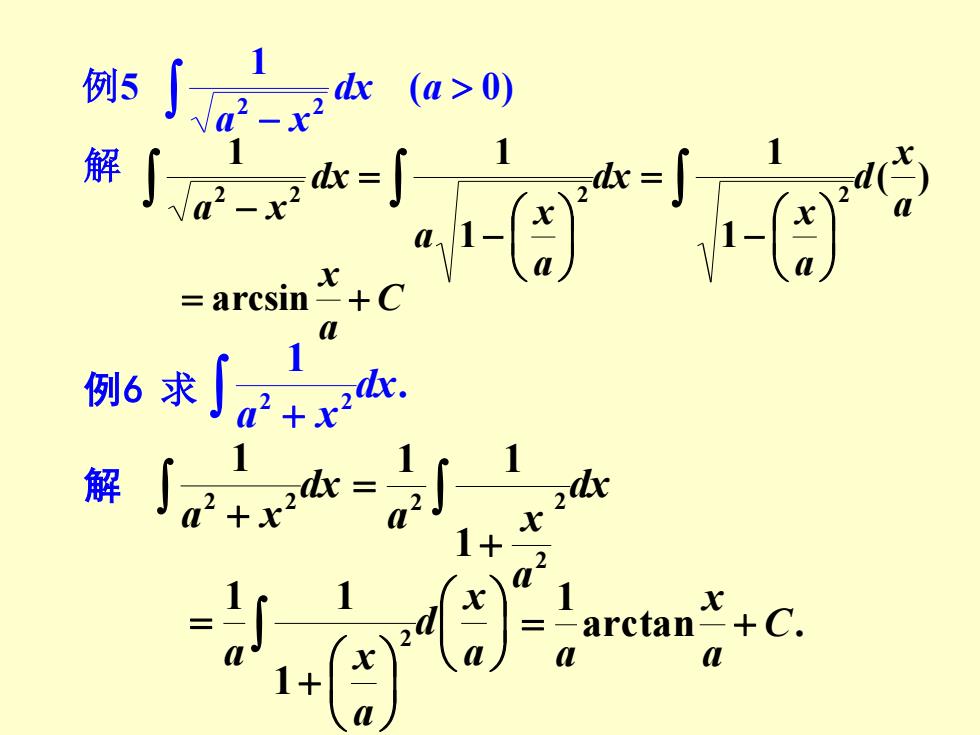
例5 ∫-xa>0 eo 解 arcsin 6求∫十、 dx =arctan+C. L
例5 − ( 0) 1 2 2 dx a a x 解 − = − dx a x a dx a x 2 2 2 1 1 1 ( ) 1 1 2 a x d a x − = C a x = arcsin + 例6 求 . 1 2 2 dx a x + 解 dx a x + 2 2 1 dx a a x + = 2 2 2 1 1 1 + = a x d a a x 2 1 1 1 arctan . 1 C a x a = +