
自动控制原理 三种响应之间的关系 输入 输出 60 折 T Vt) 1-e t-T0-e为 结论:对于线性定常系统,在零初始条件下,若输入 信号间呈导数或积分的关系,则其对应输出之间也呈 导数或积分的关系。积分时,积分时间常数由c(0)=0 确定。对应课本P87页表3-2旁边
自动控制原理 三种响应之间的关系 结论:对于线性定常系统,在零初始条件下,若输入 信号间呈导数或积分的关系,则其对应输出之间也呈 导数或积分的关系。积分时,积分时间常数由c(0)=0 确定。对应课本P87页表3-2旁边
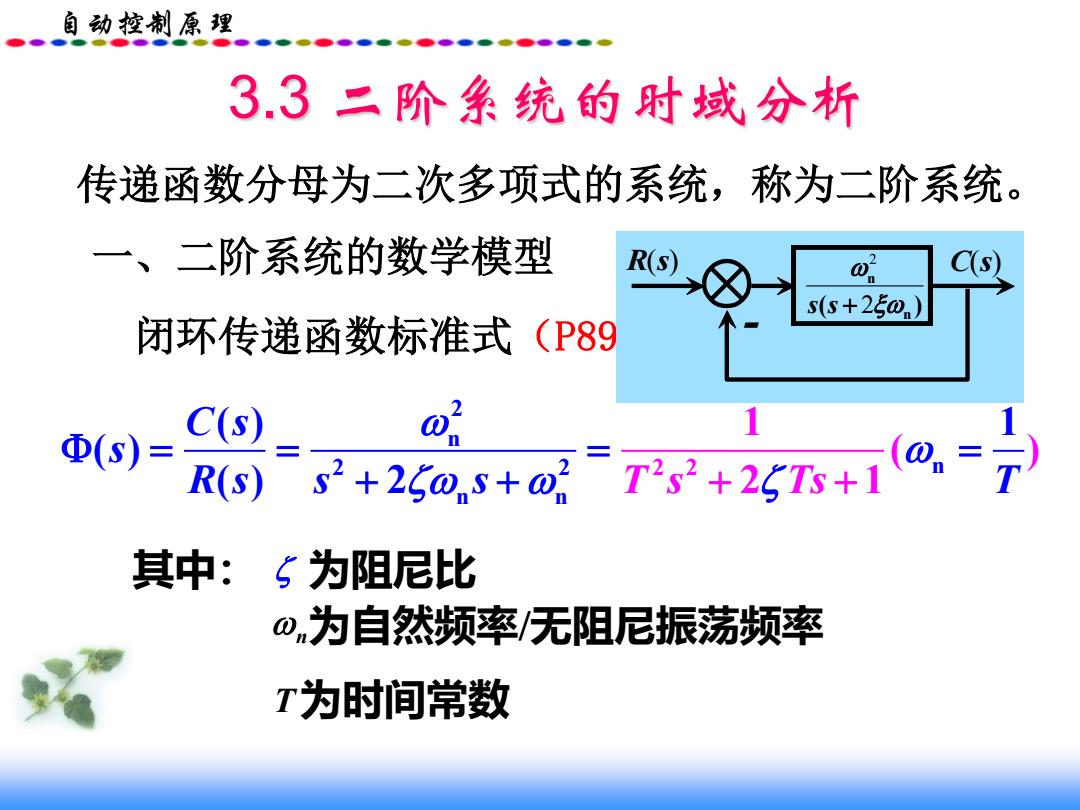
自动控制原理 3.3二阶系统的时域分析 传递函数分母为二次多项式的系统,称为二阶系统。 一、二阶系统的数学模型 R(s) s(+25w 闭环传递函数标准式(P89 Φ(S)= C(s) 2 R(s) s2+250s+02 T+255+@=7 其中:5为阻尼比 ωn为自然频率/无阻尼振荡频率 T为时间常数
自动控制原理 3.3 二阶系统的时域分析 传递函数分母为二次多项式的系统,称为二阶系统。 一、二阶系统的数学模型 闭环传递函数标准式(P89 式(3-11)) 2 n 2 2 n n n 2 2 ( ) 1 1 ( ) ( ) ( ) 2 2 1 C s s R s s s T s Ts T + = + + + = = = 2 2 n n s s( ) + R(s) C(s) - 其中: 为阻尼比 n 为自然频率/无阻尼振荡频率 T 为时间常数

自动控制原理 特征方程: S2+250nS+0n2=0 特征根: 32=-50n±0nV52-1 2、二阶系统单位阶跃响应 0,2 1 C(S)=(sRs)=g2+260.5+0,8 (2+250ns+on2)-s(s+250n)1 s2+250nS+0n2 S 1 5+250m ss2+260nS+①n1 1 一十 C2 S S-S1 S-S2 c(t)=1+ce"+ce
自动控制原理 2 2 2 0 n n 特征方程: s s + + = 特征根: 2 1 2 1 . n n s = − − 2、二阶系统单位阶跃响应 2 2 2 2 2 2 2 2 2 1 2 1 2 1 ( ) ( ) ( ) . 2 ( 2 ) ( 2 ) 1 . 2 1 2 2 1 n n n n n n n n n n n C s s R s s s s s s s s s s s s s s s c c s s s s s = = + + + + − + = + + + = − + + = + + − − 1 2 1 2 ( ) 1 s t s t c t c e c e = + +