例2:m-k振动系统,输入外打(0),输出()() 求其动力学方程。 y10 y2(0 m2 2 m2 ky m戊+y+k2(y-2)=f(I) m m2j2=k2(y-2)(2) k(4-)
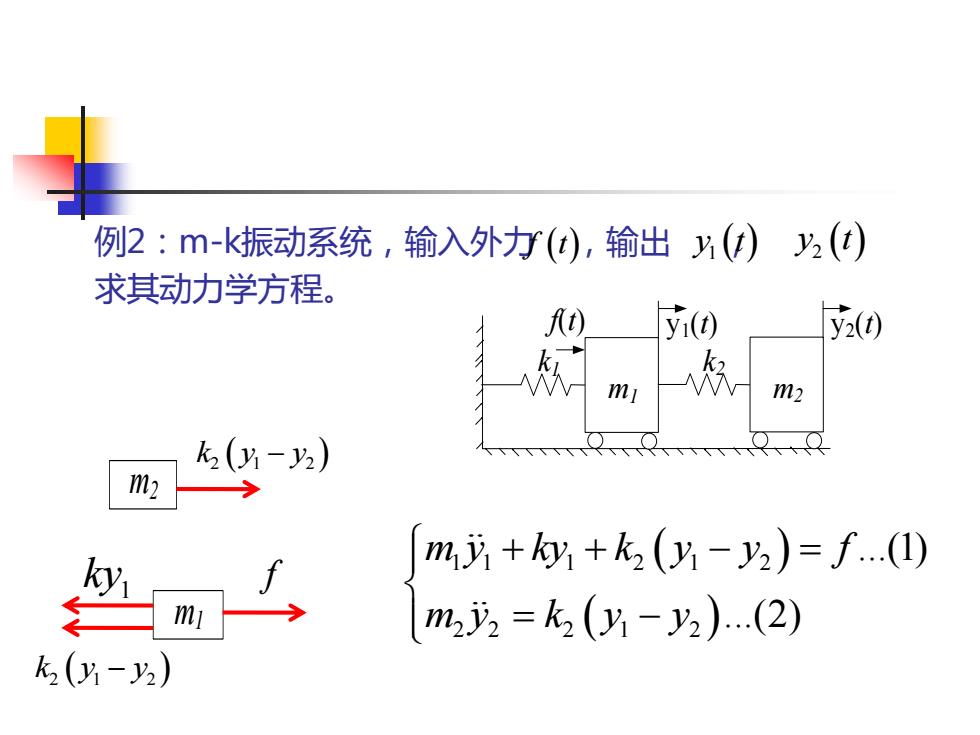
例2:m-k振动系统,输入外力 ,输出 , 求其动力学方程。 f t( ) y t 1 ( ) y t 2 ( ) ( ) ( ) 1 1 1 2 1 2 2 2 2 1 2 .(1) .(2) m y ky k y y f m y k y y + + − = = − k1 m1 k2 m2 f(t) y1(t) y2(t) m2 k y y 2 1 2 ( − ) m1 f 1 ky k y y 2 1 2 ( − )

三系统非线性微分方程的线性化(略)P31页 四列写系统微分方程的一般步骤: 1.分析系统工作原理和系统中各变量间的关系,确定系统的 输入量和输出量。 2从系统的输入端开始,依物理定律,依次列写系统各元件 的动力力学方程,其中要考虑相邻元件间的负载效应。 3.将各方程式中的中间变量消去,求出输入量一输出量间的 微分方程 4.在列写微分方程时,对非线性项进行线性化处理
三.系统非线性微分方程的线性化(略)P31页 四.列写系统微分方程的一般步骤: 1.分析系统工作原理和系统中各变量间的关系,确定系统的 输入量和输出量。 2.从系统的输入端开始,依物理定律,依次列写系统各元件 的动力力学方程,其中要考虑相邻元件间的负载效应。 3.将各方程式中的中间变量消去,求出输入量—输出量间的 微分方程 4.在列写微分方程时,对非线性项进行线性化处理

§2.2拉普拉斯(Laplace)变换 1.熟悉L变换的定义 2.典型函数的拉氏变换 要求{ 3.拉氏变换的基本原理 4.部分分式展开式及待定系数法 5.查L表 1.方便求解,以时间表示的微分方程变为以S表示的代数方程 2.对零初始条件下,引入传递函数和传递矩阵的概念,直接 在复(频)域中研究系统的动态特性,以及对系统进行综合、 校正,具实际意义
§2.2 拉普拉斯(Laplace)变换 1.熟悉L变换的定义 2.典型函数的拉氏变换 3.拉氏变换的基本原理 4.部分分式展开式及待定系数法 5.查L表 1.方便求解,以时间表示的微分方程变为以S表示的代数方程 2.对零初始条件下,引入传递函数和传递矩阵的概念,直接 在复(频)域中研究系统的动态特性,以及对系统进行综合、 校正,具实际意义。 要求

一拉氏变换的定义 若孔)为的函数,且t<0时,)=0,则)的拉氏变换 定义为: F(S)=L[f()]=0f(e"t 象函数 原函数
若f(t)为t的函数,且t<0时, f(t) =0,则f(t)的拉氏变换 定义为: ( ) ( ) ( ) 0 st F S L f t f t e dt − = = 象函数 一 .拉氏变换的定义 原函数

二.一些常用函数的拉氏变换 0 ) 1.单位阶跃函数 t<0 t≥0 →t F(S)=L[u()]=u(te "d=e"di
1.单位阶跃函数 ( ) ( ) ( ) 0 0 st st F S L u t u t e dt e dt − − = = = ( ) 0 0 1 0 t u t t = 二.一些常用函数的拉氏变换 u(t) t a 0 1 1 st e S S − = − =