《高等数学》课程教学资源（讲稿，上册）第6章第5讲（二阶微分方程求解）

0O00一、二阶常系数齐次线性微分方程r2+pr+q=0.(3)当△=p2-4q<0时，特征方程有一对共轭复根，特征值为rz=α±βi这时微分方程y"+py'+qy=0有两个复数形式的线性无关解：J = e(a+βi)x = eax.ebix, J, = e(α-β)* =eax.e-Bix.我们希望能得到实值函数形式的解，根据欧拉公式ei=cosθ+isinの，上述复数特解可改写为J=ea*(cos βx+isin βx),J2=ea(cosβx-isin βx)111由定理6.1知，取y=+=e**cosx 2 ==eaxsinβx212iy与y,是原方程的两个线性无关的特解.因此，方程y+py+qy=0的通解为y=ea*(C,cosβx+C,sinβx)

一、二阶常系数齐次线性微分方程 6 1 2 e ( cos sin ). x y C x C x      （3） 2 1 2 当  p  4q  0时，特征方程有一对共轭复根，特征值为r，   i.这时微分 方程y   py   qy  0有两个复数形式的线性无关解： ( i) i ( i) i 1 2 e e e e e e x x x x x x y y          ，    . i e cos isin  我们希望能得到实值函数形式的解，根据欧拉公式    ，上述复数 特解可改写为 1 2 e (cos isin ) e (cos isin ) x x y x x y x x       ，     1 1 2 2 1 2 1 1 1 1 e cos e sin 2 2 2i 2i x x y y y x y y y x   由定理6.1知，取     ，     ，则 1 2 y 与y 是原方程的两个线性无关的特解.因此，方程y   py   qy 0 的通解为 2 r  p r  q  0

OAO一、二阶常系数齐次线性微分方程二阶常系数齐次线性微分方程y"+py'+qy=0的通解的求解过程如下(1)将原方程化为标准形式：y"+py'+qy=0写出y+py'+qy=0的特征方程+pr+q=0，求得特征根π.(2)(3)按照下表得到y"+py+qy=0的通解y"+py+qy=O的通解y"+py'+qy=O的特征根y=Ce" +C,e'sx两个不等的实根ry=(C +C,x)e*两个相等的实根r=r=r两个共轭复根ri2=α±iy=ea*(C, cos x + C, sin βx)

一、二阶常系数齐次线性微分方程 7 二阶常系数齐次线性微分方程y   py   qy  0 的通解的求解过程如下： （1） 将原方程化为标准形式：y   py   qy  0. 2 1 2 （2） 写出y   py   qy  0 的特征方程r  pr  q  0，求得特征根r， r . （3） 按照下表得到y   py   qy  0 的通解. y   py   qy  0的特征根 y   py   qy  0的通解 1 2 两个不等的实根r≠r 两个共轭复根r1，2 ＝α±iβ 1 2 两个相等的实根r＝r＝r

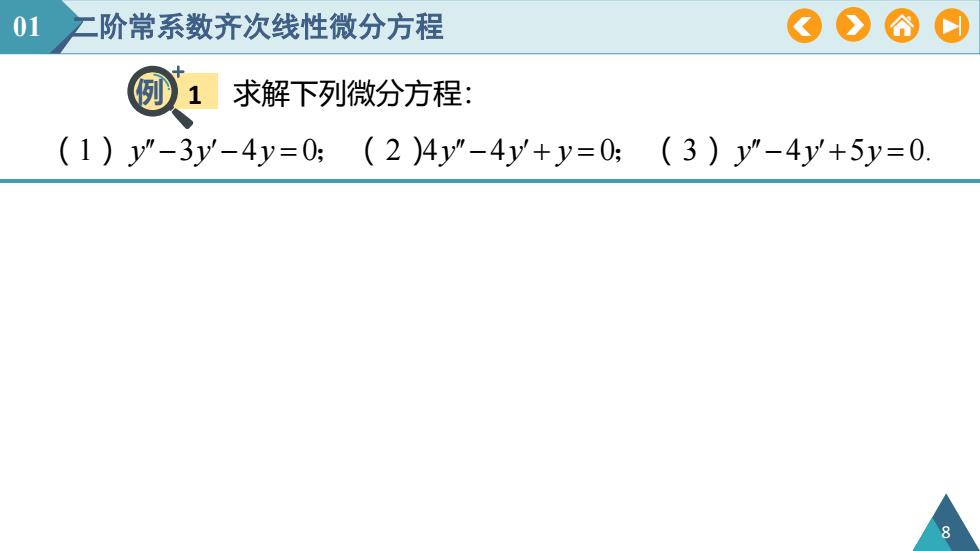
01OAO阶常系数齐次线性微分方程例1求解下列微分方程：(1) y"-3y'-4y=0;（3）y"-4y'+5y=0(2 )4y"-4y'+y=0;8

例 1 （ 1 ）y3y4y  0；（ 2 ）4y4y y  0；（ 3 ）y4y5y  0. 求解下列微分方程： 01 二阶常系数齐次线性微分方程 8

01OAO二阶常系数齐次线性微分方程例1求解下列微分方程：1(1） y"-3y'-4y=0;(2)4y"-4y'+y=0;(3） y"-4y'+5y=0解（1）原方程的特征方程为r2-3r-4=0，特征根为r=4，r=-1,因此原方程的通解为y=C,e4*+C,e-*(2）原方程可化简为"-'+=特征方程为r2-r+CM特征根为r=r=，因此原方程的通解为y=(C+C,x)e,(3）原方程的特征方程为r22-4r+5=9特征根为r=2+i,r2=2-i，因此原方程的通解为y=e2(C,cosx+C,sinx)

例 1 解 （ 1 ）y3y4y  0；（ 2 ）4y4y y  0；（ 3 ）y4y5y  0. 求解下列微分方程： （1）原方程的特征方程为r 2 3r  4  0，特征根为 1 2 r  4，r  1， 4 1 2 e e x x y C C  因此原方程的通解为   . （2）原方程可化简为 ， 1 0 4 y y y  2 1 0 4 特征方程为 r  r   ， 特征根为 1 2 1 2 r  r  ， 2 1 2 ( )e . x 因此原方程的通解为y  C C x （3）原方程的特征方程为r 2 4r 5  0， 2r  2i ， 2 1 2 e ( cos sin ). x 因此原方程的通解为 y  C x C x 1 特征根为 r  2i， 01 二阶常系数齐次线性微分方程 9

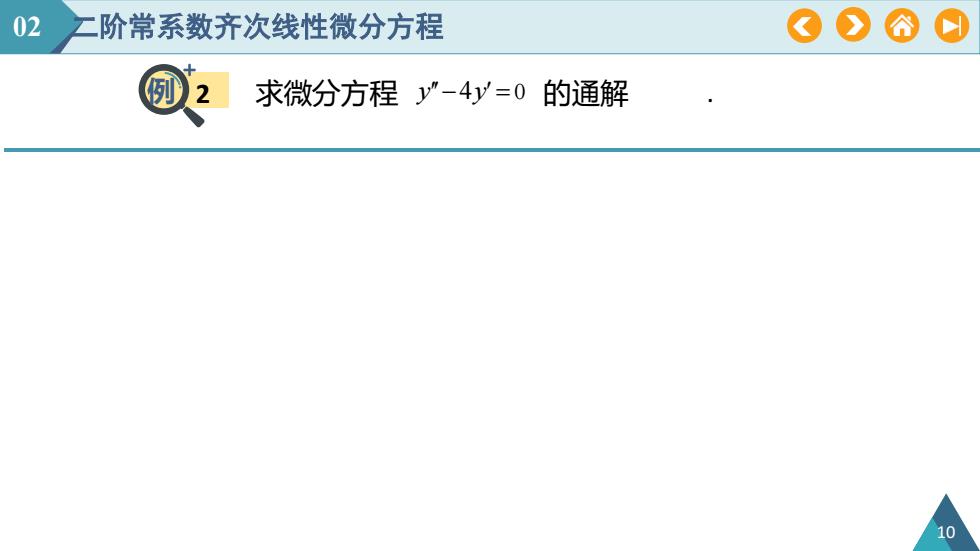
02阶常系数齐次线性微分方程A例求微分方程"-4y=0 白的通解10

例 2 02 二阶常系数齐次线性微分方程 10 求微分方程 y4y  0 的通解