《线性代数》课程教学资源（教案讲义，A）第四章 线性方程组 4-2齐次线性方程组

教学课型：理论课实验课口习题课口第42课实践课口技能课口其它口主要教学内容（注明：*重点#难点：齐次线性方程组解的结构，通解表达式，重点：齐次线性方程组解的结构，求解齐次线性方程组难点:齐次线性方程组基础解系教学目的要求：（1）理解齐次线性方程组解的性质、结构、通解表达式；（2）会求解齐次线性方程组教学方法和教学手段：课堂讲授，多媒体与板书相结合讨论、思考题、作业：参考资料：同济大学编《线性代数》高等教育出版社

第 4-2 课 教学课型：理论课  实验课□ 习题课□ 实践课□ 技能课□ 其它□ 主要教学内容（注明：* 重点 # 难点 ）： 齐次线性方程组解的结构，通解表达式. 重点： 齐次线性方程组解的结构，求解齐次线性方程组. 难点： 齐次线性方程组基础解系. 教学目的要求： （1）理解齐次线性方程组解的性质、结构、通解表达式； （2）会求解齐次线性方程组. 教学方法和教学手段： 课堂讲授，多媒体与板书相结合 讨论、思考题、作业： 参考资料： 同济大学编 《线性代数》 高等教育出版社

$4.2齐次线性方程组设齐次线性方程组au+ai2x2+...+ainx,=0a2ixj+a2x2+...+a2nx,=0(4-5)amX,+am2X2+...+ammx,=0其系数矩阵[aua12ain.a22a21a2n.A=amlamnam2令[0][x]0X20:x=[o][x.则线性方程组（4-5）的矩阵方程形式为Ax =0.(4-6)显然，线性方程组（4-5）总是有解的若x,x2，,x为（4-5）的解，则XX2x =[xn]是（4-6）的解，也是线性方程组（4-5）的解向量，线性方程组（4-5）的解向量具有下面两个重要性质，性质1两个解向量的和仍然是解向量，即设与，5是（4-5）的解向量，则5+52也是（4-5）的解向量.证只需验证气与，满足线性方程组（4-6）即可.因为与15，是（4-5）的解向量，所以A=0，A,=0,而A(5+52)=A5+A52=0+0=0.故1,5,满足

§4.2 齐次线性方程组 设齐次线性方程组                  0 0 0 1 1 2 2 2 1 1 2 2 2 2 1 1 1 1 2 2 1 m m mn n n n n n a x a x a x a x a x a x a x a x a x （4-5） 其系数矩阵                     m m mn n n a a a a a a a a a A 1 2 2 1 2 2 2 1 1 1 2 1 . 令               n x x x x 2 1 ，               0 0 0 0 . 则线性方程组（4-5）的矩阵方程形式为 Ax  0. （4-6） 显然，线性方程组（4-5）总是有解的. 若 n x , x , , x 1 2  为（4-5）的解，则               n x x x x 2 1 是（4-6）的解，也是线性方程组（4-5）的解向量. 线性方程组（4-5）的解向量具有下面两个重要性质. 性质 1 两个解向量的和仍然是解向量，即设 1 2  , 是（4-5）的解向量，则  1  2 也是（4-5）的解向量. 证 只需验证 1 2  , 满足线性方程组（4-6）即可.因为 1 2  , 是（4-5）的解 向量，所以 A 1  0，A 2  0 ，而 A( 1  2 )  A 1  A 2  0  0  0.故 1 2  , 满足

（4-6），即为（4-5）的解向量性质2一个解向量的倍数仍为解向量，即设=是（4-5）的解向量，是任意数，则也是（4-5）的解向量.证由于A()=(A)=0=0，所以（4-5）的解向量，由性质1,2知，齐次线性方程组（4-5）的解向量的线性组合仍是（4-5）的解向量，即设52，52…5.,都是（4-5）的解向量，M,2，...入.-为任意数，则5+2252+.+n5n-仍是（4-5）的解.因此，方程组（4-5）的全部解向量构成个一个向量空间，称为方程组（4-5）的解空间，它是R"的一个子空间.如果方程组（4-5）有非零解，由性质1,2知，它一定有无穷多非零解.要求出（4-5）的所有解，只需求出解空间的一个基就行了。下面我们来给出求解空间的一个基的一种方法设线性方程组（4-5）系数矩阵A的秩r(<n)，不妨假设A的前r个列向量线性无关，于是A的行最简形为[1..0br.. bu01bmbr+1...I :00000..00与I对应的线性方程组为[xi=-b1r+++ ..- b.,X,(4-7)X, =-b,r+Xr+ -...-br,nXn显然，线性方程组（4-5）与（4-7）同解在（4-7）中，任给xr+1，×，一组值，可唯一确定X,X2…X,的值，就得到（4-7）的一个结，也就是（4-5）的解，我们把x+.…x成为自由未知量.令x..X,分别取下列n-r组数：

（4-6），即为（4-5）的解向量. 性质 2 一个解向量的倍数仍为解向量，即设  是（4-5）的解向量，  是任 意数，则  也是（4-5）的解向量. 证 由于 A( )  (A)  0  0 ，所以  （4-5）的解向量. 由性质 1,2 知，齐次线性方程组（4-5）的解向量的线性组合仍是（4-5）的 解向量，即设     nr , , , 2 2 都是（4-5）的解向量，   nr , , 1 2 为任意数，则 1 1  2 2  nr nr 仍是（4-5）的解.因此，方程组（4-5）的全部解向量 构成个一个向量空间，称为方程组（4-5）的解空间，它是 n R 的一个子空间. 如果方程组（4-5）有非零解，由性质 1,2 知，它一定有无穷多非零解.要求 出（4-5）的所有解，只需求出解空间的一个基就行了. 下面我们来给出求解空间的一个基的一种方法. 设线性方程组（4-5）系数矩阵 A 的秩 r( n) ,不妨假设 A 的前 r 个列向量线 性无关，于是 A 的行最简形为                                            0 0 0 0 0 0 0 0 0 1 1 0 1 1 1 1 rr rn r n b b b b I . 与 I 对应的线性方程组为                   r r r r r n n r r n n x b x b x x b x b x , 1 1 , 1 1, 1 1 1, （4-7） 显然，线性方程组（4-5）与（4-7）同解.在（4-7）中，任给 r n x , , x 1  一组值， 可唯一确定 r x , x , x 1 2 的值，就得到（4-7）的一个结，也就是（4-5）的解，我 们把 r n x , , x 1  成为自由未知量. 令 r n x , , x 1  分别取下列 n  r 组数：

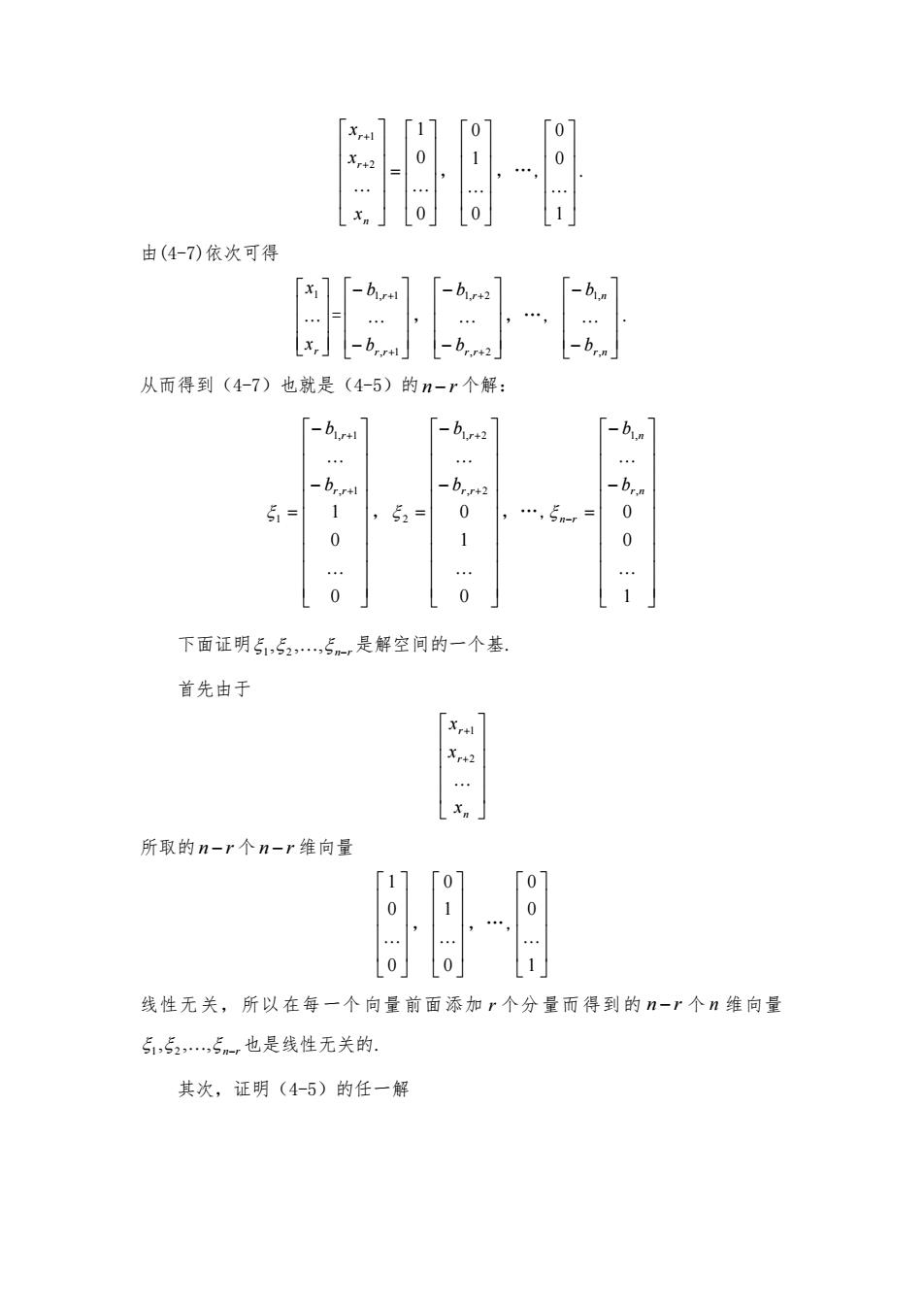
0Ar+0L1?由（4-7)依次可得1Db.x,-brart-b.从而得到（4-7）也就是（4-5）的n-r个解：[ br,[- b1r2[-b..]........- br+-br+2-bra5i =100，52 =, Sn-r =010.00下面证明5，5.，5是解空间的一个基首先由于[x+Xr+2Xn所取的n-r个n-r维向量00001线性无关，所以在每一个向量前面添加r个分量而得到的n-r个n维向量51,52,..5.-,也是线性无关的其次，证明（4-5）的任一解

                             0 0 1 2 1 n r r x x x ，              0 1 0 ，.,              1 0 0 . 由(4-7)依次可得            r x x1 =                , 1 1, 1 r r r b b ，                , 2 1, 2 r r r b b ，.,              r n n b b , 1, . 从而得到（4-7）也就是（4-5）的 n  r 个解：                              0 0 1 , 1 1, 1 1 r r r b b  ，                              0 1 0 , 2 1, 2 2 r r r b b  ，.,                             1 0 0 , 1, r n n n r b b  下面证明     nr , , , 1 2 是解空间的一个基. 首先由于                n r r x x x 2 1 所取的 n  r 个 n  r 维向量              0 0 1 ，              0 1 0 ，.,              1 0 0 线性无关，所以在每一个向量前面添加 r 个分量而得到的 n  r 个 n 维向量     nr , , , 1 2 也是线性无关的. 其次，证明（4-5）的任一解

元2r5=2r+.+[n]都可以由51，52.…5-,线性表示.为此，构造向量n= r+15 +Ar+252 +...+an5n-r?由于51,52,5m-,是（4-5）的解，故n也是（4-5）的解。比较n与=知，他们的后面n-r个分量对应相等，而线性方程组（4-7）表明它的任一解的前r个分量可由后n-r个分量唯一确定，因此n=，即5=Ar15,+2r+252+...+An5n-r这样就证明了51,52，5-是解空间的一个基，从而知解空间的维数是n-r.上面给出了一种求解空间的基的方法.当然，求基的方法很多，而解空间的基也不唯一，事实上方程组（4-5）的任意n-r个线性无关的解向量，都可以作为解空间的基，方程组（4-5）解空间的基又称为方程组的基础解系当方程组（4-5）的系数矩阵的秩R(A)=n时，方程组（4-5）只有零解，因而没有基础解系（此时解空间只有一个零向量）；当R(A)=r<n时，方程组（4-5）必有含n-r个向量的基础解系，设求得51,52,…,5.-,为方程组（4-5）的一个基础解系，则（4-5）的任一解x可表示为X=k;5, +k252+...+kn-r5n-r.其中k,k2..,kn为任意常数.上式称为方程组（4-5）的通解，此时解空间可表示为[x=k,5i+k252+...+kn-r5n-r|kj,k2...,kn-r为任意常数]

                        n r r      1 1 都可以由     nr , , , 1 2 线性表示.为此，构造向量   r1 1  r2 2  n nr ， 由于     nr , , , 1 2 是（4-5）的解，故  也是（4-5）的解.比较  与  知，他们的 后面 n  r 个分量对应相等，而线性方程组（4-7）表明它的任一解的前 r 个分量 可由后 n  r 个分量唯一确定，因此    ，即   r1 1  r2 2  n nr 这样就证明了     nr , , , 1 2 是解空间的一个基，从而知解空间的维数是 n  r . 上面给出了一种求解空间的基的方法.当然，求基的方法很多，而解空间的 基也不唯一，事实上方程组（4-5）的任意 n  r 个线性无关的解向量，都可以作 为解空间的基. 方程组（4-5）解空间的基又称为方程组的基础解系. 当方程组（4-5）的系数矩阵的秩 R(A)  n 时，方程组（4-5）只有零解，因 而没有基础解系（此时解空间只有一个零向量）；当 R(A)  r  n 时，方程组（4-5） 必有含 n  r 个向量的基础解系，设求得     nr , , , 1 2 为方程组（4-5）的一个基 础解系，则（4-5）的任一解 x 可表示为 n r n r x k k k  1 1  2 2     . 其中 n r k k k   , , , 1 2 为任意常数.上式称为方程组（4-5）的通解，此时解空间可表 示为 { n r n r x k k k  1 1  2 2     | n r k k k   , , , 1 2 为任意常数}