
单位切向量 r(s=1 ∴定义曲线的单位切向量:T(s)=r'(s) P(o)
单位切向量 ( ( ) ) ( ) s s s T r r =1 定义曲线的单位切向量:
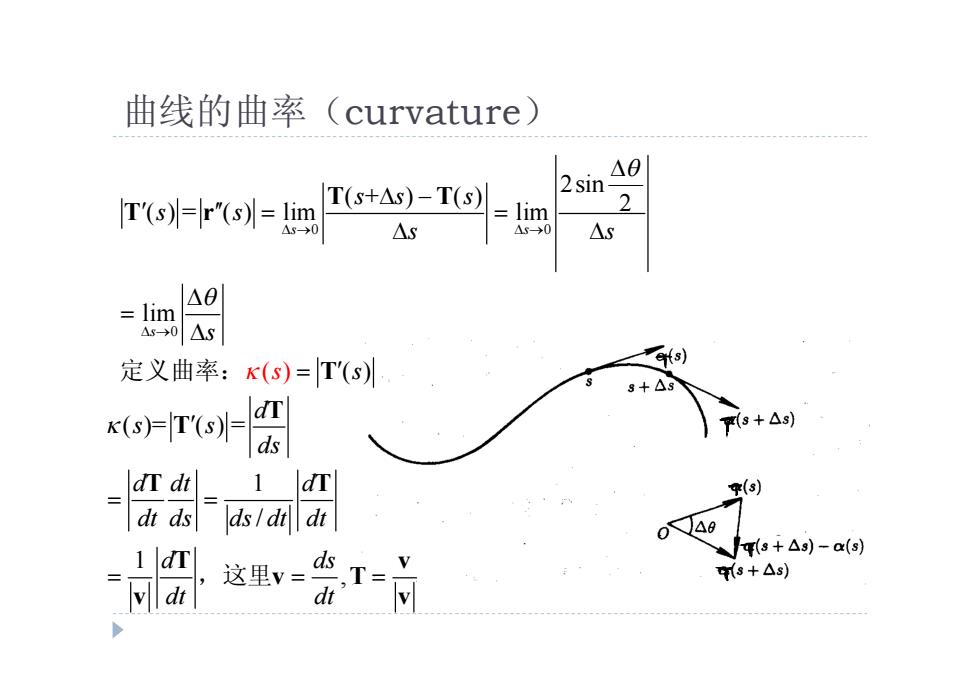
曲线的曲率(curvature) △0 (s)=r(s)= T(s+As)-T(s) 2sin =lim 2 4 △s lim △0 △s 定义曲率:K(s)=T'(s) s+△3 K(s)片T'(s)= s+△s) dr dt 1dr () dt ds dsldt dt 1dr s+△s)-a(s) 这里v= d s+△s) d .T=Y
曲线的曲率(curvature) 0 0 0 2sin ( + ) ( ) 2 ( ) = ( ) lim lim lim ( ) ( ) s s s s s s s s s s s s s T T T r 定义曲率: T ( )= ( ) = 1 / 1 , d s s ds d dt d dt ds ds dt dt d ds dt dt T T T T T v v T v v ,这里

例 直线的曲率是0 半径为的圆周的曲率为 a 1、r(t)=(a,b) 2、r0)=(acost,a.sin,v=在=(←-asint.,acos) dt =V(-asin))2+(acos)}=a T前-人sn1o小g=←gsnn
例 0 1 a a 直线的曲率是 半径为 的圆周的曲率为 2 2 1 ( )=( , ) 2 ( ) ( cos , sin ), sin , cos = sin cos sin ,cos , ( cos , sin ) 1 1 ( ) t a b d t a t a t a t a t dt a t a t a d t t t t dt d s dt a r r r v v v T T v T v 、
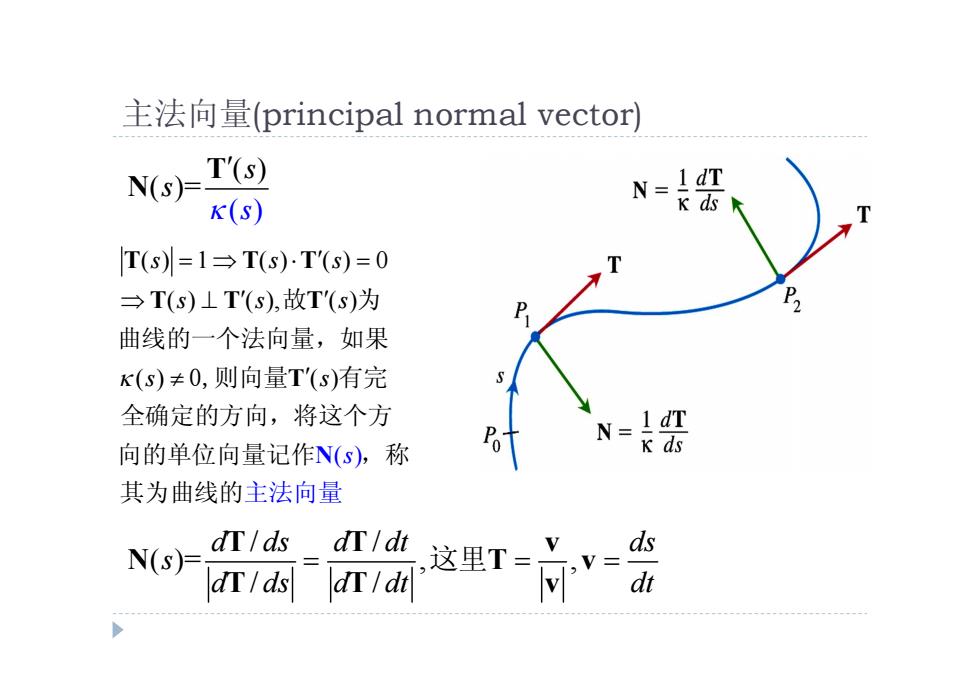
主法向量(principal normal vector)) N(s)= T'(s) N=IdT k(s) K ds T(s=1→T(s)T'(s)=0 →T(s)⊥T'(s),故T'(s)为 P 曲线的一个法向量,如果 K(s)≠0,则向量T'(s)有完 全确定的方向,将这个方 N=IdT 向的单位向量记作N(s),称 K ds 其为曲线的主法向量 N(s)= dr/ds dr/dt 这里T= ds dT/ds dr/dt dt
主法向量(principal normal vector) ( ) ( ) = ( ) s s s T N ( ) 1 ( ) ( ) 0 ( ) ( ), ( ) ( ( ) ( ) ) s s s s s s s s s N T T T T T T T 故 为 曲线的一个法向量,如果 0,则向量 有完 全确定的方向,将这个方 向的单位向量记作 ,称 其为曲线的主法向量 / / ( )= , , / / d ds d dt ds s d ds d dt dt T T v N T v T T v 这里
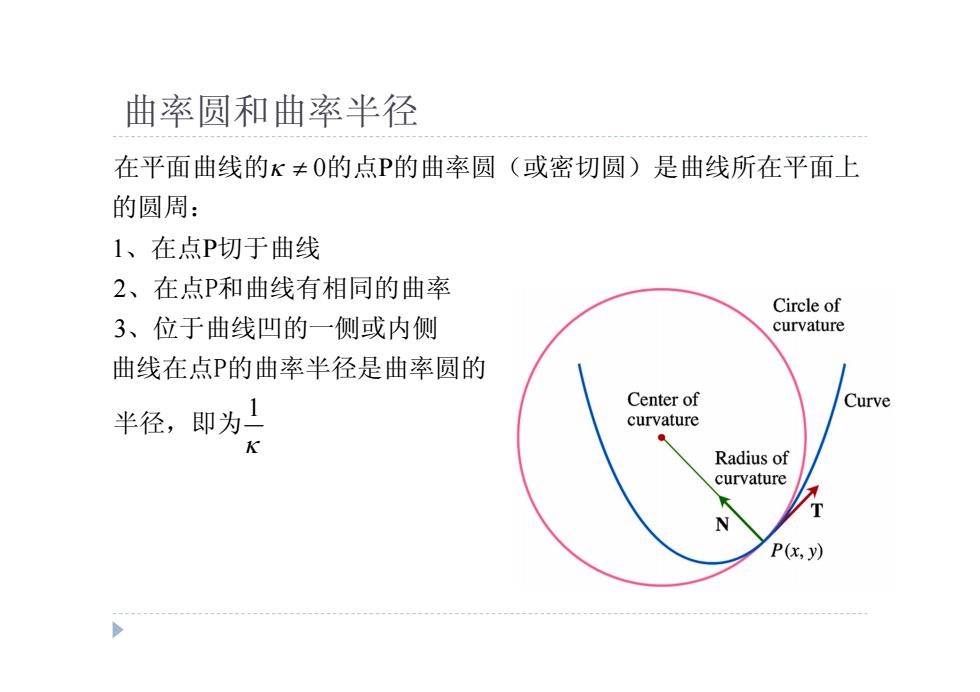
曲率圆和曲率半径 在平面曲线的K≠O的点P的曲率圆(或密切圆)是曲线所在平面上 的圆周: 1、在点P切于曲线 2、在点P和曲线有相同的曲率 Circle of 3、位于曲线凹的一侧或内侧 curvature 曲线在点P的曲率半径是曲率圆的 Center of Curve 半径,即为 curvature ● Radius of curvature T N P(x,y)
曲率圆和曲率半径 0 P 1 P 2 3 1 在平面曲线的 的点 的曲率圆(或密切圆)是曲线所在平面上 的圆周: 、在点 切于曲线 、在点P和曲线有相同的曲率 、位于曲线凹的一侧或内侧 曲线在点P的曲率半径是曲率圆的 半径,即为