华东理工大学：《信号与系统》课程教学资源（课件讲稿）第三章 傅里叶变换 §3.5 傅里叶变换的性质 Properties of Fourier Transform

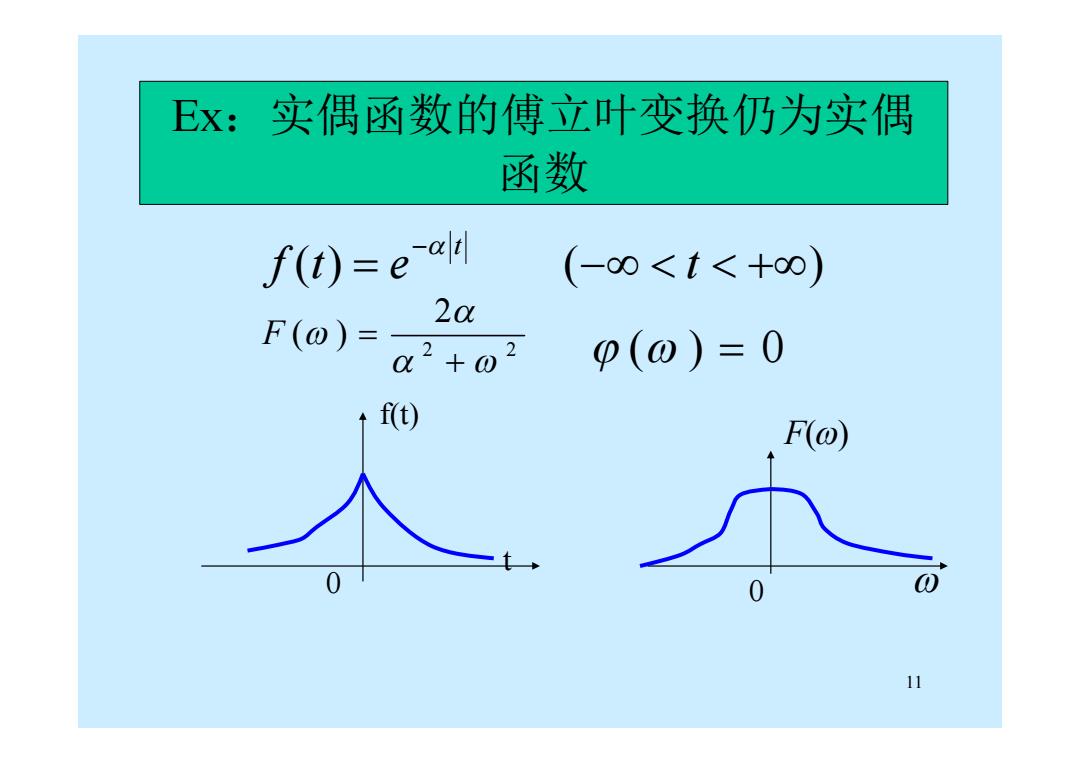
Ex:实偶函数的傅立叶变换仍为实偶 函数 f(t)=e-al (-0<t<+0) 20 F(0)= a2+02 p(0)=0 f(t) F(@ 11

11 f(t) 0 t  F() 0 ( )  (   )  f t e t  t 2 2 2 ( )      F   ( )  0 Ex：实偶函数的傅立叶变换仍为实偶 函数

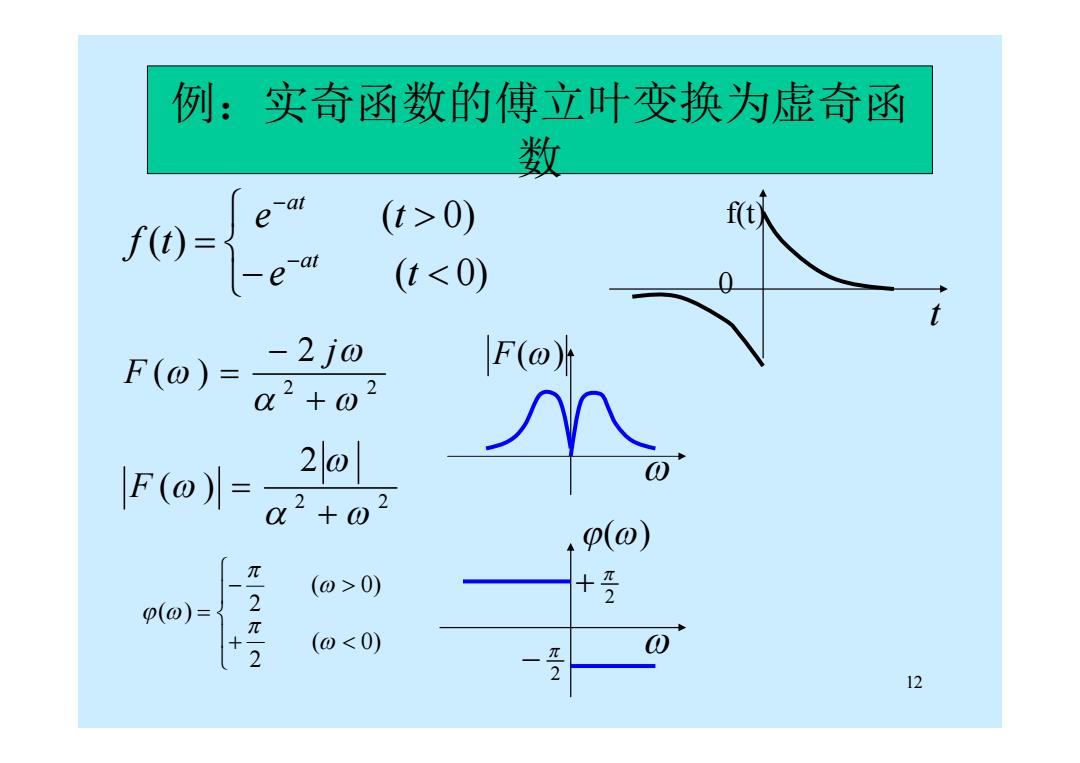
例：实奇函数的傅立叶变换为虚奇函 数 0- e (t>0) f(t) (t<0) F(o)= -2j0 F(o片 u2+02 1F(o= (0>0) π p(o)= 2元2 (0<0) π2 12

12 2 2 2 ( )        j F           ( 0) 2 ( 0) 2 ( )                ( 0) ( 0) ( ) e t e t f t at at t f(t) 0 2 2 2 ( )      F  F()  例：实奇函数的傅立叶变换为虚奇函 数  2   2   ()

3、对称性Duality 若已知 F(@)=FT f(t) 则 FTF(t)]=2r f(-@) 证明： fW=n了F()w-de F)d f-o)rewh FT[F(t)]=2f(-w) 13

13 3、对称性 Duality 若已知 则         f t F e d j t ( ) 2 1 ( ) ( ) , 2 1 ( )           f t F e d j t      f   F t e dt j t   ( ) 2 1 ( ) FT F (t)  2f ( ) 证明： F ( )  FT f (t) FTF(t)  2 f ()

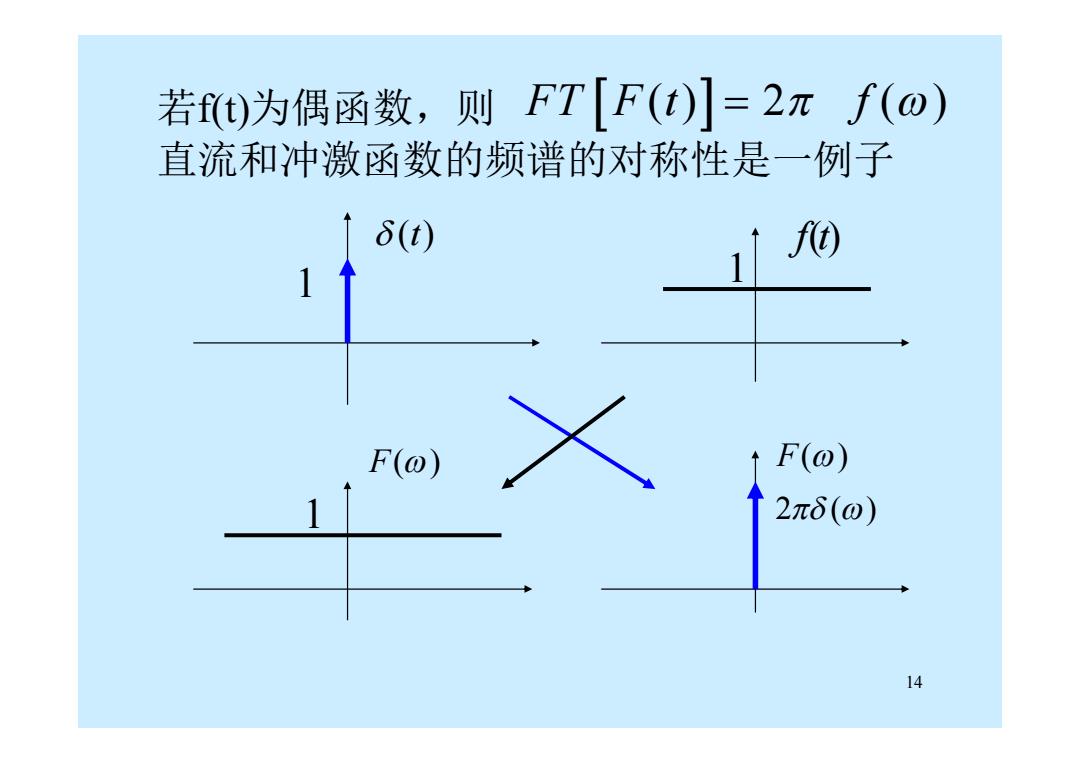
若f)为偶函数，则FT[F(t)]=2πf(o) 直流和冲激函数的频谱的对称性是一例子 6(t) F(o) F(o) 2πδ(o) 14

14 若f(t)为偶函数，则 直流和冲激函数的频谱的对称性是一例子  (t) 1 1 f(t) 1 F() 2 () F() FT F t f  ( ) 2 ( )    

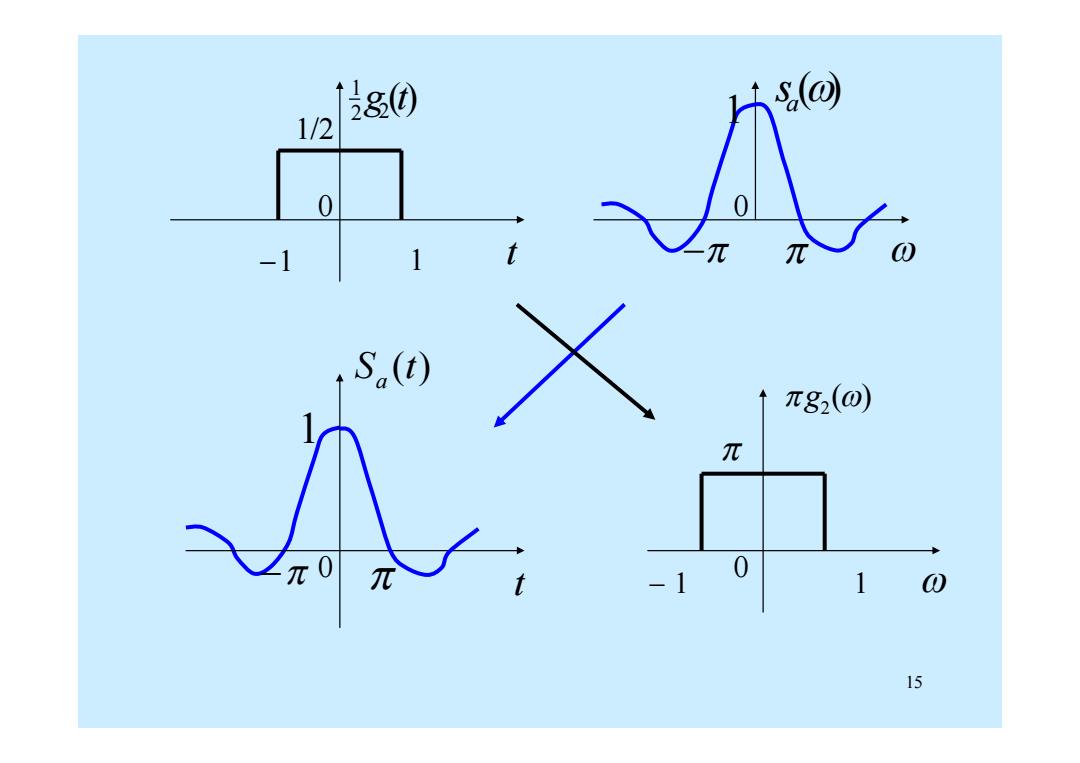
8@ so 1/2 0 0 -1 1 S.(t) π82(o) π -1 1 15

15 () 2 2 1 g t 1 1 t 1/2 0 () a s    1 0 S (t) a   t 1 0 ( ) g2   1 1   0