华东理工大学：《信号与系统》课程教学资源（课件讲稿）第三章 傅里叶变换 §3.5 傅里叶变换的性质 Properties of Fourier Transform

a>1,t>0 1 f(t)-e-a F(o)= FT a+jw f换成 掇 F F(@)=FT =2 a+jt t换成 称 O F(o)=2Wf(-w)=2πe +a0 16

16 FT   a j F   1 ( ) ? 1 ( ) 1         a jt F  FT 对 称 性      a F f e  ( )  2 ( )  2 1 at f t e  ( )  a 1, t  0 t 换成  f 换成 F1 换 成 t 

4、尺度变换特性Time Scaling 若 FTLf(t)]=F(@) 则 nra1=白5（号） 17

17 4、尺度变换特性 Time Scaling • 若 • 则 FT[ f (t)]  F() ( ) 1 [ ( )] a F a FT f at  

证明：根据定义，有 FT[f(at)]=f(at )e-i'dt 令x=at,则dt=。d, 当a>0时 FT[f(at]=∫f(x)e dx a =F() 当a<0时 FT[f(a)=∫f(x)ed =-F() 18

18 证明：根据定义，有 令 ,则 ， 当 时 当 时 FT f at f at e dt j t        [ ( )] ( ) x  at dt dx a 1  a  0 1 [ ( )] ( ) j x a F T f at f x e dx a       ( ) 1 a F a   a  0 1 [ ( )] ( ) j x a F T f at f x e dx a       ( ) 1 a F a   

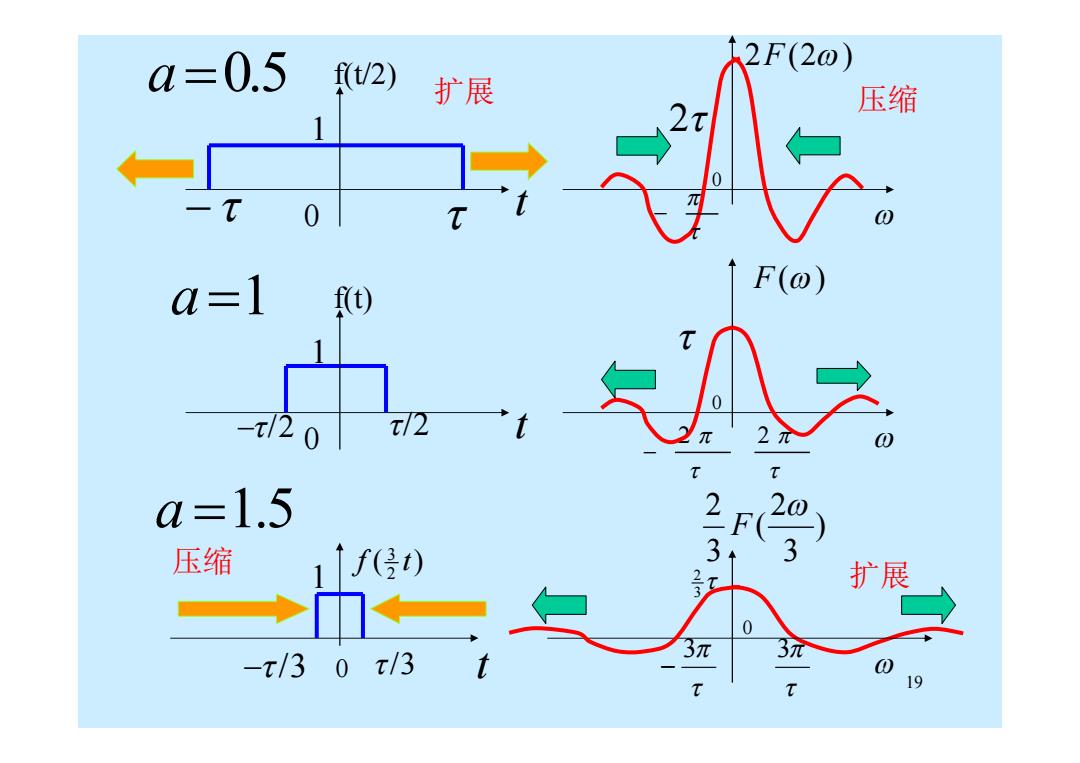
a=0.5 f(/2) 太2F(20) 扩展 压缩 0 0 a=1 F(⊙) f(t) -t201 2一 =1.5 2 压缩 11f(30) 3 扩展 →巾 0 -t/30x/3t 3π T 19

19  /3 0  /3 t  3  3  扩展  压缩 ( ) 2 3 f t ) 3 2 ( 3 2  F 3 1 2 0 a 1.5  2   2   f(t) 0 t F()  /2 /2 0  1 a1 2F(2) f(t/2) 0 t 2      0  1 a0.5 扩展 压缩

5、时移特性Time Shifting 若 FT [f (t)]=F(@) 则 FT[f(t±t)]=F(o)eo 证明：x=t-to FT[f(x】=f(ax)ea+o'd -fe dx=eF(o) .FT[f(t-t】=eooF(w) 20

20 5、时移特性 Time Shifting 若 则 证明： 0 x  t  t  ( ) ( ) 0 0   FT f t t e F  j t    FT f ( t )   F ( )   0 0 ( ) ( ) j t F T f t t F e      ( ) ( ) 0 0     e f x e dx e F j t j x j t        FTf x  f x e dx j x t       ( ) 0 ( ) ( ) 