非线性物理:孤波物理 g+号a+g+)+g12-)=0 现在来建立边界条件。对于水槽底部或水槽四壁: On 建立如图所示二维坐标系,则边界 条件变成: p,=0z=h,+n 如果流体流动过程按照行波处理,则假设波长为l,c=(g)2为 近似波速,重新进行变量变换:
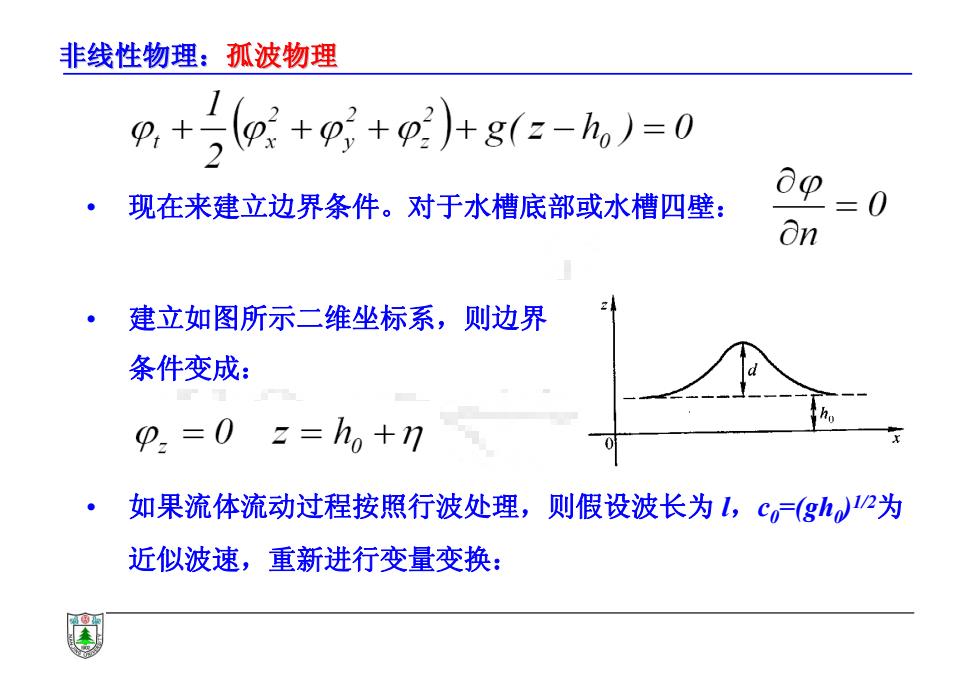
非线性物理:孤波物理 • 现在来建立边界条件。对于水槽底部或水槽四壁: • 建立如图所示二维坐标系,则边界 条件变成: • 如果流体流动过程按照行波处理,则假设波长为 l,c0=(gh0)1/2为 近似波速,重新进行变量变换:

非线性物理:孤波物理 x =lx',z=hoz',t lt'/co n dn',p=gldp'/co 。 经过这个变化后所有变量都是无量纲的,将它们代入Laplace方程 和边界条件,然后再去掉撇号,得到新的方程和边界条件: Bpx+pz=0(0<z<1+on》 9:=0fz=0 7,+C07x-p:/B=0 fz=1+07 7,+9,+p2/2+ap:/2B=0 B=h/12,a=d/h
非线性物理:孤波物理 • 经过这个变化后所有变量都是无量纲的,将它们代入Laplace方程 和边界条件,然后再去掉撇号,得到新的方程和边界条件:

非线性物理:孤波物理 下面推导在长波长(hP<1)和小振幅(dh<1)近似下上述约 化方程的解。前人证明,对于一个x的解析函数f作,x),方程: Bo+=0 的通解总是可以表示成: p=∑-1) (2m10x2m 代入到下面边界条件: 7,+0φ7x-p./B=0 讨z=1+07 7,+9,+p/2+p:/2B=0
非线性物理:孤波物理 • 下面推导在长波长(=h02/l2<<1)和小振幅(d/h0<<1)近似下上述约 化方程的解。前人证明,对于一个 x 的解析函数 f(t,x),方程: 的通解总是可以表示成: • 代入到下面边界条件:

非线性物理:孤波物理 分别得到:7,+[1+7)f1 6t+an+a0+afi]小+wg')=0 ·和: ++- 号(U+an}pfm+a4.fm-af)+0B)=0 因为<1,<1,略去B和aB等高阶项,令F=f,然后将上 式对x求导,化简后得到:
非线性物理:孤波物理 • 分别得到: • 和: • 因为<<1,<<1,略去 2 和 等高阶项,令 F=fx,然后将上 式对 x 求导,化简后得到:

非线性物理:孤波物理 n,+[(1+a7)Fl-BF=0 F,aFFs+nx _BF=0 2 ·取函数F为下列形式: F=7- 2 0C7+ 代入上述方程并只取、的一次项,则两个方程化成一个方程: 7+7.+27m.+ G=
非线性物理:孤波物理 • 取函数 F 为下列形式: • 代入上述方程并只取、的一次项,则两个方程化成一个方程: