
(uvw)'u'vw uv'w+uvw →fx川=xf(x).fn(x) +.+f(x)f2(x).f(x) =∑Πfx)f(x)为 i=1 k=1 k≠i 作为(2)的特殊情况 若v=c,则(cu'=cW或[Cf(x)'=Cf'(x); 即常数因子可以提到导数符号的外面 fr-2)
(uvw) = uvw + uvw + uvw ( ) ( ); ( ) ( ) ( ) [ ( )] ( ) ( ) ( ) 1 1 1 2 1 2 1 = = = = + + = n i n k i k i k n n n i i f x f x f x f x f x f x f x f x f x ④ 作为(2)的特殊情况 若v = c,则(cu) = cu 或 [Cf (x)] = Cf (x); 即常数因子可以提到导数符号的外面 [ ( )] ( ) 1 1 k f x k f x n i i i i n i i = = =

即线性组合的导数等于导数的线性组合 —说明求导是一线性运算 ⑤作为(3)的一种特殊情况, 若=1则中= 二、例题分析 例1求y=x3-2.x2+sinx的导数. 解 y'=3x2-4x+c0sx
即线性组合的导数等于导数的线性组合 ——说明求导是一线性运算 ⑤作为(3)的一种特殊情况, 2 ) 1 1, ( v v v u 若 = 则 = − 二、例题分析 例1 2 sin . 求 y = x 3 − x 2 + x的导数 解 2 y = 3x − 4x + cos x

例2求y=sin2xlnx的导数. 解 .y =2sinx.cosx.Inx y'=2c0sx·cosx·lnx+2sinx·(-sinx)·lnx +2sinx·cosx· x 1 =2cos 2x Inx+sin 2x. X 例3求y=tanx的导数. 解y=a=(0空
例 2 求 y = sin 2x ln x的导数 . 解 y = 2sin x cos x ln x y = 2cos x cos x ln x + 2sin x (− sin x) ln x x x x 1 + 2sin cos sin 2 . 1 2cos 2 ln x x = x x + 例 3 求 y = tan x的导数 . 解 ) cos sin = (tan ) = ( xx y x
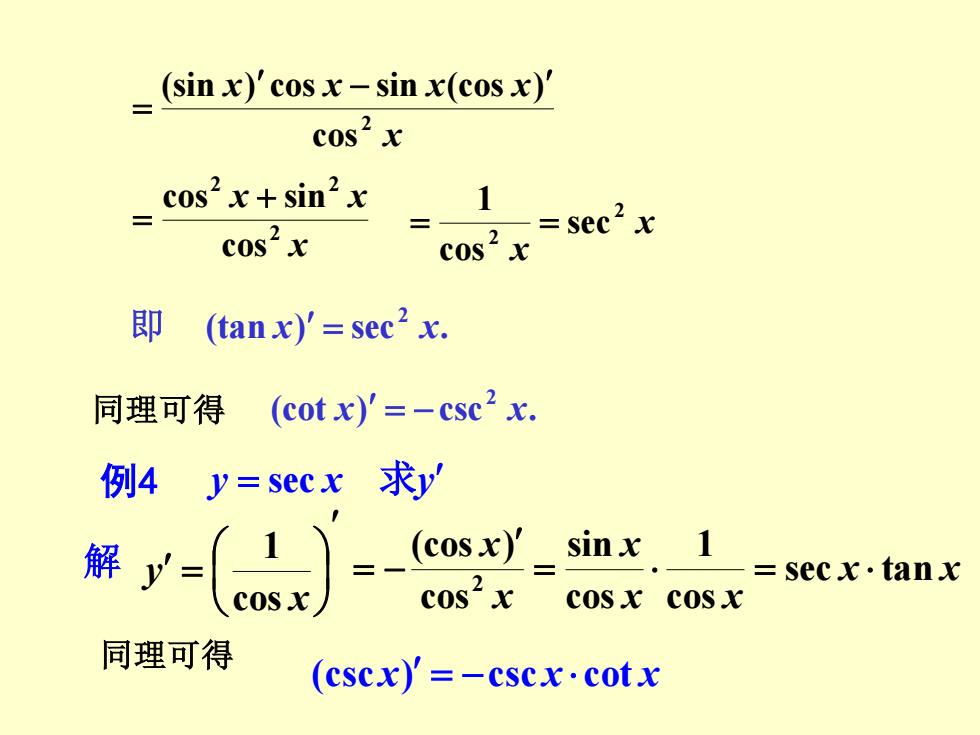
(sin x)'cosx-sin x(cosx)' cos2 x cos'x+sin'x cos2x -=sec2x cos 即 (tanx)'=sec2 x. 同理可得(C0tx)'=-csc2x. 例4y=secx求y' 部r-(e=-oa cos2x cosx cosx 同理可得 (cscx)'=-cscx·cotx
x x x x x 2 cos (sin ) cos − sin (cos ) = x x x 2 2 2 cos cos + sin = x x 2 2 sec cos 1 = = (tan ) sec . 2 即 x = x 同理可得 (cot ) csc . 2 x = − x 例4 y = sec x 求y 解 = x y cos 1 x x 2 cos (cos ) = − x x x x x sec tan cos 1 cos sin = = 同理可得 (cscx) = −csc x cot x
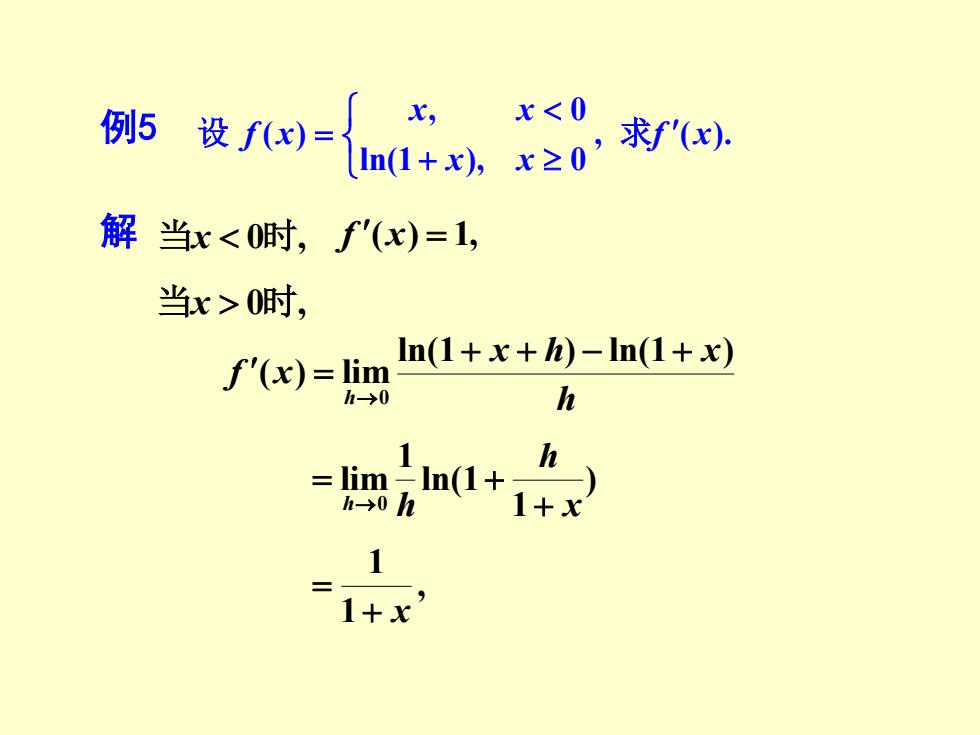
s设-{0n 解当x<0时,f'(x)=1, 当x>0时, ln(1+x+-ln(1+x) f(x)=lim →0 h 1+x
例 5 , ( ). ln(1 ), 0 , 0 ( ) f x x x x x f x + 设 = 求 解 当 x 0 时 , f ( x ) = 1 , 当 x 0 时 , h x h x f x h ln(1 ) ln(1 ) ( ) lim0 + + − + = → ) 1 ln( 1 1 lim0 x h h h + = + → , 1 1+ x =