
CIEECAU1.020-↓02图4.4.2根据卷积的定义,可以确定()的宽度为1,幅度为1,f,()的宽度为3,幅度为1。我们容易得到2singF(o)= -2sin 30F,(o)=,由时域卷积定理可得又由()=()*f,()F(o)= F(o) F,(o)4sngsm02如果在本题中,信号1C)是三角波的形式,那么就应该将了)分解成两个相同宽度的矩形脉冲的卷积。例4.5已知信号1(0)-7, sinm sin2,*r()( am(元解在求解这一类的定积分时,应该考虑傅利叶变换的以下性质:F(0)= rr()dt若(lim (0)=0) 10)-F(0)0若(lim F(o)=0) ora(orda设()-[sin2m) (sin2m)元(元
CIEE CAU 根据卷积的定义,可以确定 f ( )t 1 的宽度为 1,幅度为 1, f (t) 2 的宽度为 3,幅度为 1。 我们容易得到 ( ) ω ω ω 2 2sin F1 = ( ) ω ω ω 2 3 2sin F2 = 又由 f () () () t f t f t 1 2 = ∗ ,由时域卷积定理可得 ( ) ( ) ( ) 2 1 2 2 3 sin 2 4sin ω ω ω ω ω ω = F = F ⋅ F 如果在本题中,信号 f ( )t 是三角波的形式,那么就应该将 f (t) 分解成两个相同宽度的 矩形脉冲的卷积。 例 4.5 已知信号 ( ) t t t t f t t π π π sinπ sin 2 = ⋅ ⋅ 求 dt t t t t 2 2 2 sin sin 2 ⋅ ⋅ ∫ +∞ −∞ π π π π 的值 解 在求解这一类的定积分时,应该考虑傅利叶变换的以下性质: F( ) () f t dt ∫ +∞ −∞ 0 = (lim ( ) = 0) →±∞ f t t 若 ( ) ( ) ω ω π f t F d ∫ +∞ −∞ = 2 1 (lim ( ) = 0) →±∞ F ω t 若 ( ) ( ) ω ω π f t dt F d ∫ ∫ +∞ −∞ +∞ −∞ = 2 2 2 1 设 ( ) ⋅ = t t t t f t π π π sin 2π sin 2 1 () f t 2 t 2 3 − 2 3 2 1 − ( ) f t 1 o t 2 1 1 图 4 .4 .2
CAUCIE由于sinm αG.(o)m2maG.根据频域卷积定理,可得F(0)= 2元_Gz (0)*Gs (0)F(o)如图4.5.1所示。Fe)2元图4°5又由()=f(),根据频域微分定理,可得F(o)-小%5()F(o)的波形图如图 3.5. 2 所示。F()图4.5.2由于信号{(0)是实信号,即有2(0)=(0)-"()=(0)2,因此Cr () (cr)a=r(d='dt因此本题求的实际信号()的总能量,而根据帕斯瓦尔定理,可得
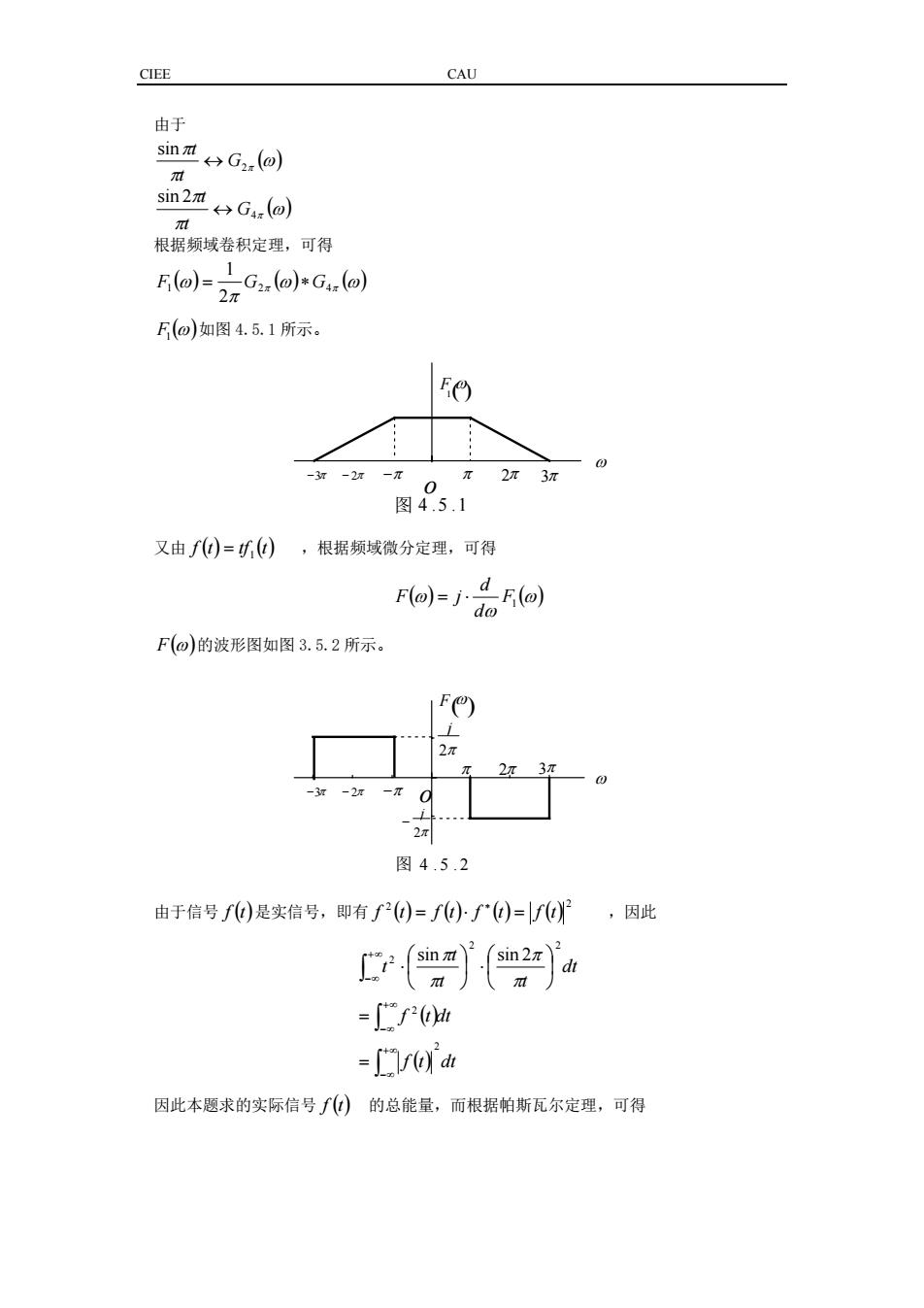
CIEE CAU 由于 ( ) ω π π 2π sin G t t ↔ ( ) ω π π 4π sin 2 G t t ↔ 根据频域卷积定理,可得 ( ) () () ω ω π 1 ω 2π 4π 2 1 F = G ∗G F1( ) ω 如图 4.5.1 所示。 又由 f () () t tf t = 1 ,根据频域微分定理,可得 ( ) ( ) ω ω ω F1 d d F = j ⋅ F( ) ω 的波形图如图 3.5.2 所示。 由于信号 f ( )t 是实信号,即有 ( ) ( ) ( ) ( ) 2 2 f t = f t ⋅ f t = f t ∗ ,因此 ( ) f ( )t dt f t dt dt t t t t 2 2 2 2 2 sin sin 2 ∫ ∫ ∫ +∞ −∞ +∞ −∞ +∞ −∞ = = ⋅ ⋅ π π π π 因此本题求的实际信号 f ( )t 的总能量,而根据帕斯瓦尔定理,可得 −3π 3π ( )ω1 F o ω − 2π −π π 2π 图 4 .5 .1 2π j − 2π j 图 4 . 5 . 2 − 2π 2π −π π ω o ( ) F ω 3π −3π