
第二章器件的偏差与失配 其中费米电势 4=k灯in n (2.5) NN, Q为MOS管耗尽区中储存的电荷浓度,有 Q。=√2qNac(24+VsB)) (2.6) 它们都是与温度有关的量,当温度改变时,阈值电压将会随之改变。 电阻的阻值也是与温度相关的,而且是复杂的非线性的关系[8]。将它们的 关系展开为多项式,如果对精度要求不高或者温度变化不大,可以只给出多项式 的前两项,有 R(T)=R(T。)[1+10-6TC(T-T。)】 (2.7) 其中R(刀为温度T下的电阻值,R(T)是另外某个温度To下的电阻值,TC是电 阻温度系数(TCR,Temperature Coefficient of Resistivity),用百万分之一每摄氏 度(ppm/C)表示,所以上式中有一个10的系数。 如果对精度要求高,则要保留前三项,有 R(T)=R(T)1+106TC,(T-T)+106TC2(T-T)2] (2.8) 其中TC1是线性电阻温度系数,TC2是二次电阻温度系数,二次电阻温度系数通 常比线性电阻温度系数小,但是温度变化大时,它对电阻影响也是很大的。 2.2.2老化的影响 集成电路在工作情况下,其通电状态和温度环境将会影响其可靠性,发生老 化现象,可能致使晶体管的阈值电压和电流发生偏移、使无源器件如电阻值发生 偏移。 在模拟电路中,场效应晶体管的可靠性主要考虑沟道热载流子(CHC Channel Hot-carrier)应力、偏置温度不稳定性(BTl,Bias Temperature Instabilities)、硬击穿和软击穿、应力致漏电流(SlLC,Stress Induced Leakage Current),电路的不同工作状态对应了不同的老化机理[9]. 以图24所示的一个p管输入的简单两级运放为例。在电路的工作模式 9
第二章 器件的偏差与失配 9 其中费米电势 A f i g A ln( ) exp( ) 2 ln c v kT N q n E N kT kT q N N (2.5) Qb为 MOS 管耗尽区中储存的电荷浓度,有 Q qN b A f SB 2 (2 ) ε V (2.6) 它们都是与温度有关的量,当温度改变时,阈值电压将会随之改变。 电阻的阻值也是与温度相关的,而且是复杂的非线性的关系[8]。将它们的 关系展开为多项式,如果对精度要求不高或者温度变化不大,可以只给出多项式 的前两项,有 6 0 0 R T R T TC T T ( ) ( )[1 10 ( )] (2.7) 其中 R(T)为温度 T 下的电阻值,R(T0)是另外某个温度 T0下的电阻值,TC 是电 阻温度系数(TCR, Temperature Coefficient of Resistivity),用百万分之一每摄氏 度(ppm/°C)表示,所以上式中有一个 10-6的系数。 如果对精度要求高,则要保留前三项,有 6 62 0 10 20 R T R T TC T T TC T T ( ) ( )[1 10 ( ) 10 ( ) ] (2.8) 其中 TC1 是线性电阻温度系数,TC2是二次电阻温度系数,二次电阻温度系数通 常比线性电阻温度系数小,但是温度变化大时,它对电阻影响也是很大的。 2.2.2 老化的影响 集成电路在工作情况下,其通电状态和温度环境将会影响其可靠性,发生老 化现象,可能致使晶体管的阈值电压和电流发生偏移、使无源器件如电阻值发生 偏移。 在模拟电路中,场效应晶体管的可靠性主要考虑沟道热载流子(CHC, Channel Hot-carrier) 应力、偏置温度不稳定性 (BTI, Bias Temperature Instabilities)、硬击穿和软击穿、应力致漏电流(SILC, Stress Induced Leakage Current),电路的不同工作状态对应了不同的老化机理[9]。 以图 2-4 所示的一个 p 管输入的简单两级运放为例。在电路的工作模式
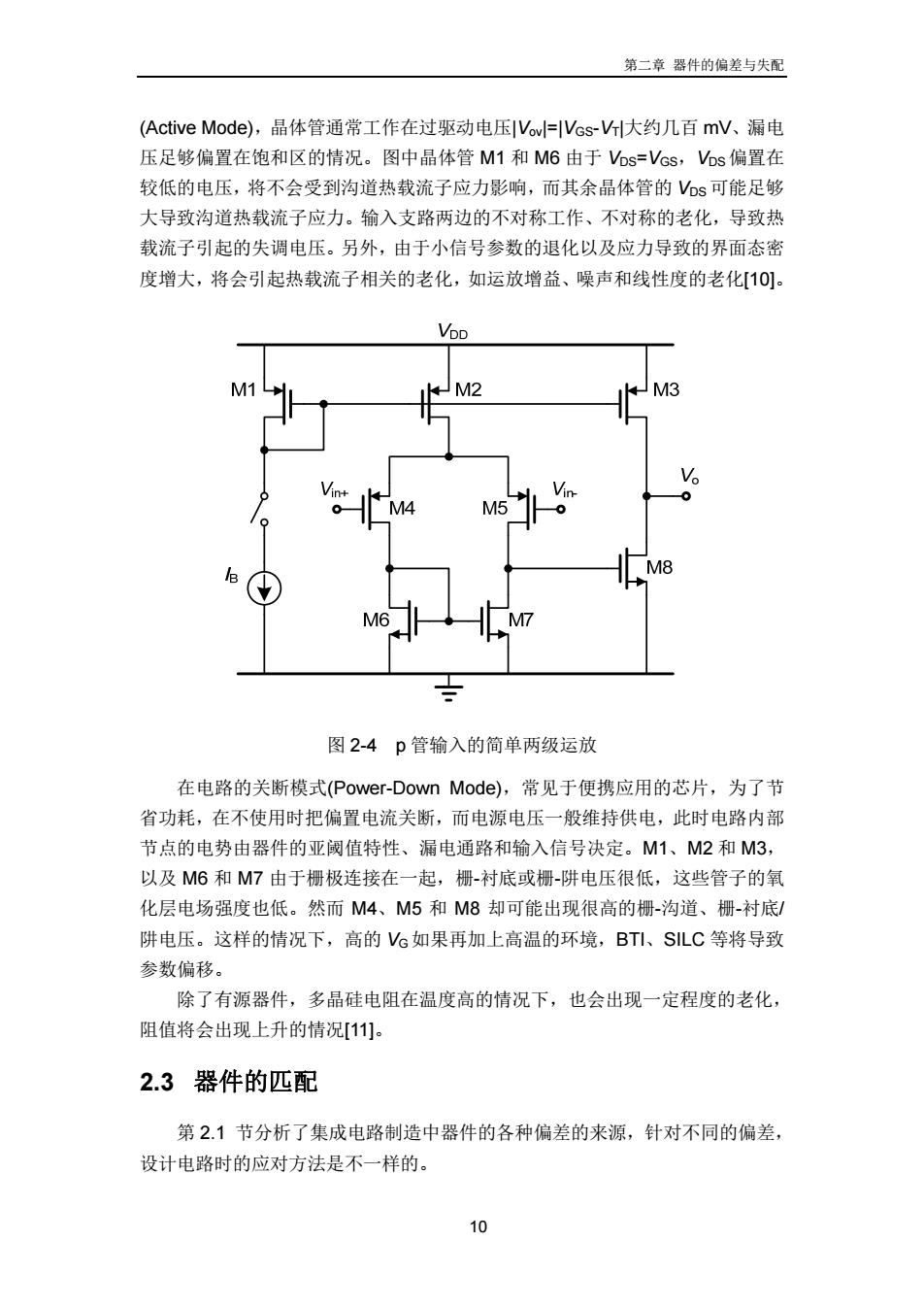
第二章器件的偏差与失配 (Active Mode),晶体管通常工作在过驱动电压IVow=Vcs-V大约几百mV、漏电 压足够偏置在饱和区的情况。图中晶体管M1和M6由于Vbs=Vcs,Vbs偏置在 较低的电压,将不会受到沟道热载流子应力影响,而其余晶体管的Vs可能足够 大导致沟道热载流子应力。输入支路两边的不对称工作、不对称的老化,导致热 载流子引起的失调电压。另外,由于小信号参数的退化以及应力导致的界面态密 度增大,将会引起热载流子相关的老化,如运放增益、噪声和线性度的老化[10]。 VDD M1 M2 M3 M8 图2-4p管输入的简单两级运放 在电路的关断模式(Power-Down Mode),常见于便携应用的芯片,为了节 省功耗,在不使用时把偏置电流关断,而电源电压一般维持供电,此时电路内部 节点的电势由器件的亚阈值特性、漏电通路和输入信号决定。M1、M2和M3, 以及M6和M7由于栅极连接在一起,栅-衬底或栅-阱电压很低,这些管子的氧 化层电场强度也低。然而M4、M5和M8却可能出现很高的栅-沟道、栅-衬底/ 阱电压。这样的情况下,高的V6如果再加上高温的环境,BT1、SLC等将导致 参数偏移。 除了有源器件,多晶硅电阻在温度高的情况下,也会出现一定程度的老化, 阻值将会出现上升的情况[11]: 2.3器件的匹配 第2.1节分析了集成电路制造中器件的各种偏差的来源,针对不同的偏差, 设计电路时的应对方法是不一样的。 10
第二章 器件的偏差与失配 10 (Active Mode),晶体管通常工作在过驱动电压|Vov|=|VGS-VT|大约几百 mV、漏电 压足够偏置在饱和区的情况。图中晶体管 M1 和 M6 由于 VDS=VGS,VDS偏置在 较低的电压,将不会受到沟道热载流子应力影响,而其余晶体管的 VDS可能足够 大导致沟道热载流子应力。输入支路两边的不对称工作、不对称的老化,导致热 载流子引起的失调电压。另外,由于小信号参数的退化以及应力导致的界面态密 度增大,将会引起热载流子相关的老化,如运放增益、噪声和线性度的老化[10]。 图 2-4 p 管输入的简单两级运放 在电路的关断模式(Power-Down Mode),常见于便携应用的芯片,为了节 省功耗,在不使用时把偏置电流关断,而电源电压一般维持供电,此时电路内部 节点的电势由器件的亚阈值特性、漏电通路和输入信号决定。M1、M2 和 M3, 以及 M6 和 M7 由于栅极连接在一起,栅-衬底或栅-阱电压很低,这些管子的氧 化层电场强度也低。然而 M4、M5 和 M8 却可能出现很高的栅-沟道、栅-衬底/ 阱电压。这样的情况下,高的 VG 如果再加上高温的环境,BTI、SILC 等将导致 参数偏移。 除了有源器件,多晶硅电阻在温度高的情况下,也会出现一定程度的老化, 阻值将会出现上升的情况[11]。 2.3 器件的匹配 第 2.1 节分析了集成电路制造中器件的各种偏差的来源,针对不同的偏差, 设计电路时的应对方法是不一样的

第二章器件的偏差与失配 其中系统偏差,它所引入的参数偏移是系统性的,对每个器件都存在,所以 使用差分电路结构、适当的偏置技术和版图技术就可以很大程度上把系统偏差的 影响降低。 对于工艺偏差,则需要设计的电路对各个工艺角不敏感。如果电路的指标和 器件参数的绝对值有关,要求器件参数有准确的大小,则要通过补偿的方法将偏 差修正,如直接对电阻电容的补偿校正、对基准电流源/电压源的温度补偿等。 而对于随机偏差,它不同于前两种偏差,由于其在设计阶段是不可预知的, 并且依赖于器件的尺寸,所以电路设计者只能通过器件的尺寸、器件的版图以及 偏置状态来控制匹配12]。 2.3.1M0S管的匹配 为了提高器件的匹配,版图上把两个器件M1、M2摆放一致,并且靠得很 近,可以认为系统偏差和工艺偏差一致,对匹配性没有影响,只考虑随机偏差。 设M1和M2各自都有偏差Vh和δB,差异为△VT和△B, △V=V,-V2 (2.9) △B=63,-6β2 (2.10) 则忽略式(2.2)和式(2.3)中的第二项,有 '(AV)=An2 (2.11) WL (48)72 A (2.12) WL 分析器件失配在电路中的影响,方法和噪声分析很相似。可以用小信号分析, 把器件的偏差δV和δ3等效成电压和电流源,如图2-5所示,V和δB的影 响等效成电压Vcs和电流Ds。 D bs+δlos V+δVT Go B+δ3 Vcs+δVcs So- (a) 11
第二章 器件的偏差与失配 11 其中系统偏差,它所引入的参数偏移是系统性的,对每个器件都存在,所以 使用差分电路结构、适当的偏置技术和版图技术就可以很大程度上把系统偏差的 影响降低。 对于工艺偏差,则需要设计的电路对各个工艺角不敏感。如果电路的指标和 器件参数的绝对值有关,要求器件参数有准确的大小,则要通过补偿的方法将偏 差修正,如直接对电阻电容的补偿校正、对基准电流源/电压源的温度补偿等。 而对于随机偏差,它不同于前两种偏差,由于其在设计阶段是不可预知的, 并且依赖于器件的尺寸,所以电路设计者只能通过器件的尺寸、器件的版图以及 偏置状态来控制匹配[12]。 2.3.1 MOS 管的匹配 为了提高器件的匹配,版图上把两个器件 M1、M2 摆放一致,并且靠得很 近,可以认为系统偏差和工艺偏差一致,对匹配性没有影响,只考虑随机偏差。 设 M1 和 M2 各自都有偏差 δVTi 和 δβi,差异为∆VT和∆β, VT T1 T2 δV δV (2.9) β δβ δ 1 2 β (2.10) 则忽略式(2.2)和式(2.3)中的第二项,有 2 2 VT T ( ) A σ V WL (2.11) 2 2 σ β ( ) Aβ β WL (2.12) 分析器件失配在电路中的影响,方法和噪声分析很相似。可以用小信号分析, 把器件的偏差 δVTi 和 δβi 等效成电压和电流源,如图 2-5 所示,δVT和 δβ 的影 响等效成电压 δVGS和电流 δIDS

第二章器件的偏差与失配 D +δV4- δbs Go × δVcs V gmV1 (δB/B)lDs So (b) 图2-5有参数偏差的MOS管及其小信号等效电路 在实际电路中,对不同的电路结构,关注的失配有所不同。比如由相同栅- 源电压偏置的晶体管之间,电流的偏差△s很重要;由相同电流偏置的晶体管之 间,栅-源电压的偏差△Vcs很重要。 A.相同Vcs偏置的晶体管匹配 如图2-6所示的电流镜,M1和M2管都由相同的电压Vcs0偏置。 △lbs=δ0s1-δ0s2 (2.13) 其中M1和M2的电流偏差△Ds1和△Ds2,各包含两部分:△V-和△B两个参数引 起的偏差。根据图2-5的模型,对于M1和M2分别有 s1=9mδVr1+ 6Blos (2.14) B 6lps2 =gmOVT2+ 6Bz-los (2.15) B MO 2 图2-6电压偏置的晶体管一一电流镜 把两式代入式(2.13)中,并整理 12
第二章 器件的偏差与失配 12 图 2-5 有参数偏差的 MOS 管及其小信号等效电路 在实际电路中,对不同的电路结构,关注的失配有所不同。比如由相同栅- 源电压偏置的晶体管之间,电流的偏差∆IDS很重要;由相同电流偏置的晶体管之 间,栅-源电压的偏差∆VGS很重要。 A.相同 VGS偏置的晶体管匹配 如图 2-6 所示的电流镜,M1 和 M2 管都由相同的电压 VGS0偏置。 DS DS1 DS2 I δI δI (2.13) 其中 M1 和 M2 的电流偏差∆IDS1和∆IDS2,各包含两部分:∆VT和∆β 两个参数引 起的偏差。根据图 2-5 的模型,对于 M1 和 M2 分别有 1 DS1 m T1 DS δβ δI g δV I β (2.14) 2 DS2 m T2 DS δβ δI g δV I β (2.15) 图 2-6 电压偏置的晶体管——电流镜 把两式代入式(2.13)中,并整理

第二章器件的偏差与失配 As=g.(6,-52)+B6Bs (2.16) =gmAVI+ 归一化后为 Alos=9mAV,+ 8 (2.17)) 忽略△V和△B的相关性,计算独立统计变量的方差,有 ()(V)) (2.18) 并由式(2.11)和式(2.12),可得 (MhsAtA (2.19) los2 可以看出相对电流失配由△V和△B贡献,两者都反比于面积的平方根,因此相 对电流失配反比于(WL)2,如果将失配减半,意味着需要把面积变成4倍。 B.差分对的匹配 图2-7所示是一个差分对,下面计算其直流失调(DC Offset)),令Vn+=Vn-, 电流失配大小△Ds满足式(2.19)。因此等效到输入失调电压Vos,有 02(4s)=g2as) 9n2 (2.20) +()A] WL 11lb2 M 图2-7简单的NMOS差分对管 13
第二章 器件的偏差与失配 13 1 2 DS m T1 T2 DS m T DS ( ) δβ δβ I g δV δV I β β gV I β (2.16) 归一化后为 DS m T DS DS I g β V I I β (2.17) 忽略∆VT和∆β 的相关性,计算独立统计变量的方差,有 2 2 DS m 2 2 2 T DS DS 2 ( ) ( ) () ( ) σ I g σ σ V β I I β (2.18) 并由式(2.11)和式(2.12),可得 2 DS m 2 2 D 2 2 VT S DS 1 [( ) ] ( ) A β σ I I W I g A L (2.19) 可以看出相对电流失配由∆VT 和∆β 贡献,两者都反比于面积的平方根,因此相 对电流失配反比于(WL) 1/2,如果将失配减半,意味着需要把面积变成 4 倍。 B.差分对的匹配 图 2-7 所示是一个差分对,下面计算其直流失调(DC Offset),令 Vin+=Vin-, 电流失配大小∆IDS满足式(2.19)。因此等效到输入失调电压 VOS,有 2 2 DS OS 2 m 2 D 2 VT S m 1 2 [ ( ( ) ] ) ( ) β σ I σ V g I A g A WL (2.20) 图 2-7 简单的 NMOS 差分对管